Snippet Topic: Metric Learning

Random Forest Distance 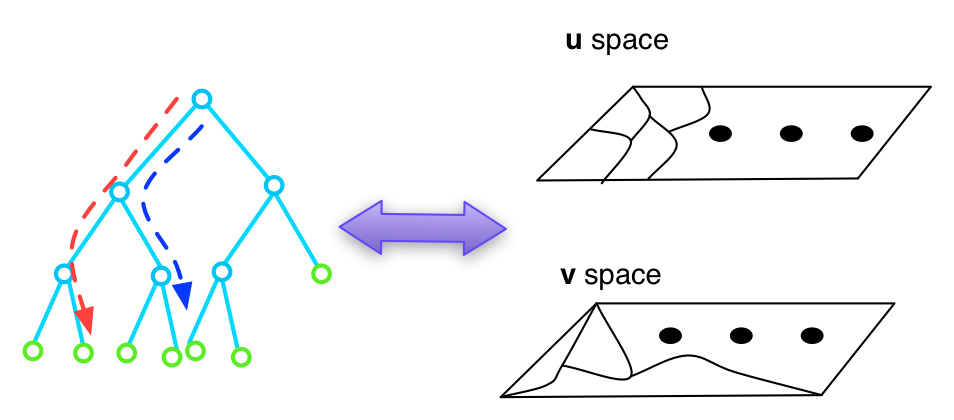Metric learning makes it plausible to learn semantically meaningful distances for complex distributions of data using label or pairwise constraint information. However, to date, most metric learning methods are based on a single Mahalanobis metric, which cannot handle heterogeneous data well. Those that learn multiple metrics throughout the feature space have demonstrated superior accuracy, but at a severe cost to computational efficiency. Here, we adopt a new angle on the metric learning problem and learn a single metric that is able to implicitly adapt its distance function throughout the feature space. This metric adaptation is accomplished by using a random forest-based classifier to underpin the distance function and incorporate both absolute pairwise position and standard relative position into the representation. We have implemented and tested our method against state of the art global and multi-metric methods on a variety of data sets. Overall, the proposed method outperforms both types of method in terms of accuracy (consistently ranked first) and is an order of magnitude faster than state of the art multi-metric methods (16x faster in the worst case).   C. Xiong, D. Johnson, R. Xu, and J. J. Corso. Random forests for metric learning with implicit pairwise position dependence. In Proceedings of ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2012. [ bib | slides | code | .pdf ]

Efficient Max-Margin Metric Learning 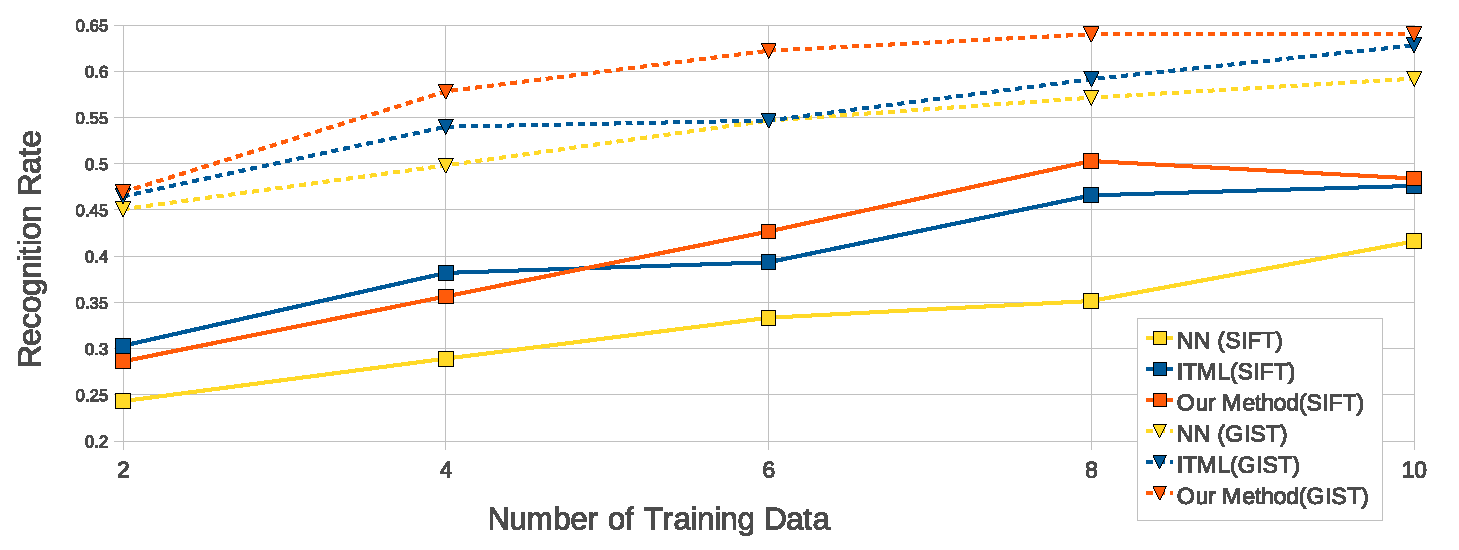Efficient learning of an appropriate distance metric is an increasingly important problem in machine learning. However, current methods are limited by scalability issues or are unsuited to use with general similarity/dissimilarity constraints. In this work, we propose an efficient metric learning method based on the max-margin framework with pairwise constraints that has strong generalization guarantee. First, we reformulate the max-margin metric learning problem as a structured support vector machine which we can optimize in linear time via a cutting-plane method. Second, we propose an approximation method for our kernelized extension based on match pursuit algorithm that allows linear-time training. We find our method to be comparable to or better than state of the art metric learning techniques at a number of machine learning and computer vision classification tasks.   C. Xiong, D. Johnson, and J. J. Corso. Efficient max-margin metric learning. In Proceedings of European Conference on Data Mining, 2012. Winner of Best Paper Award at ECDM 2012. [ bib | .pdf ]