Recitation 13
Recitation notes for the week of November 19, 2025.
-
Actually in class, we have seen a more general version, where we can make multiple calls to the black-box algorithm to solve
Bbut for this problem it is enough to make a single call.
Homework 8, Question 1
The problem
Given a graph $G$ and a number $k$, does $G$ contain a clique of size at least $k$? I.e. does there exists a subset $S\subseteq V$ such that $|S|=k$ and there are all possible $\binom{k}{2}$ edges present among the vertices in $S$?
Sample Input/Output pairs
For the sample inputs, let us consider the following graph, which we will call $G_0$:
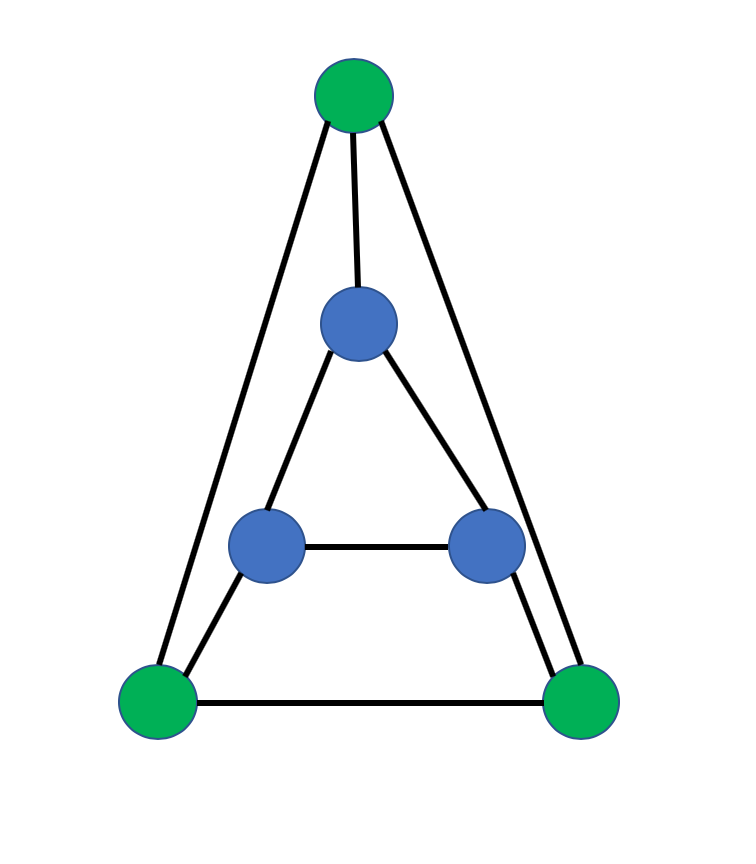
- Input: $G_0, 3$
- Output:
true(Consider the three blue nodes)
- Input: $G_0, 4$
- Output:
false(Every subset of 4 nodes has at least 2 out of the 6 edges missing)
Question 1, Part (a)
The problem
Argue that the Clique problem is in $\mathcal{NP}$.
What do we need to do to show a problem is in $\mathcal{NP}$?
To show that a problem $X$ is in $\mathcal{NP}$, you need to show that there is a witness for an input being in $X$: i.e. if $X$ on input $I$ would output true, then there would be a witness $w$ such that in polynomial time, given $I$ and $w$, one can indeed verify that $X$ on input $I$ should indeed output true. To be more precise, there exists a polynomial time function $\mathbb{V}$ (for "verifier") such that for every input $I$, there exists a polynomial-sized witness $w$ such that $\mathbb{V}(I,w)=$true if and only if $X$ on input $I$ outputs true.
Note the asymmetry above
Note the inherent asymmetry in the above condition. In particular:
- If $X$ on input $I$ outputs
true, then you just need one witness $w$ such that $\mathbb V(I,w)$=true. - If $X$ on input $I$ outputs
false, then for all witnesses $w'$, we have $\mathbb V(I,w)$=false.
Proof Idea
Recall for the problem, we are given as input a graph $G$ and an integer $k$ and we need to check if $G$ has a clique of size at least $k$ or not.
It turns out that in this case the witness for an input instance $I=(G=(V,E),k)$ is just a subset $S\subseteq V$ of size exactly $k$. We now claim that there exists a polynomial time verifier with this witness. In particular, you need to argue the following:
Exercise
Show that there exists a polynomial time verifier (i.e. an algorithm) $\mathbb V$ such that on input $G$ and a subset $S$ (as above), it outputs true if $S$ is a clique in $G$ and false otherwise.
Assuming the above is true, here is the quick argument that we want. Suppose on input $(G,k)$ the Clique problem should output true, then there has to be a subset $S^*\subseteq V$ with $|S^*|=k$ such that $S^*$ is a clique and hence we will have $\mathbb V(G,S^*)$=true, as desired. On the other hand, if the clique problem should output false for input $(G,k)$, then it has to be the case that for every $S\subseteq V$ of size $k$, $S$ is not a clique. Hence for all such $S$, we have $\mathbb V(G,S)$=false, as desired.
Question 1, part (b)
The problem
Assume that the Independent set problem on graphs on $n$ vertices and bound $k$ on the independent set (i.e. the problem is, given $G$ and $k$, does there exist an independent set of size at least $k$ in $G$?) takes time $n^{\Omega(k)}$ (for large enough $k$). Prove that the Clique problem also needs $n^{\Omega(k)}$ time to solve (for large enough $k$).
Recap of a polynomial time reduction
We review the definition of a polynomial time reduction. How this can be useful to solve part (b) is something that y'all will need to figure out on your own.
We say a problem $A$ is polynomial time reducible to a problem $B$ (denoted by $A\le_P B$) if there exists a algorithm/reduction $\mathcal{R}$ (with polynomial runtime $r(n)$) such that
- (Pre-processing step) On any input $\mathbf{x}$ for problem $A$, it computes a valid input $\mathbf{y}$ for problem $B$.
- Assuming there is a blackbox algorithm $\mathcal{B}$ for problem $B$, it then runs $\mathcal{B}(\mathbf{y})$. 1
- (Post-processing step) Based on the answer from $\mathcal{B}(\mathbf{y})$, it does some computation and outputs the answer for input $\mathbf{x}$ (for problem $A$).
The runtime of the reduction is the time take in steps 1 and 3 above and is denoted by $r(n)$ for inputs $\mathbf{x}$ of size $n$.
Now if we were to use the reduction $\mathcal{R}$ to solve the problem $A$ on input $\mathbf{x}$, what would be its total time? To answer this let $m$ be the size of $\mathbf{y}$ that is computed in step 1 above and let $T(m)$ be the runtime of the blackbox algorithm $\mathcal{B}$. Then using the above, we can solve the problem $A$ on input $\mathbf{x}$ in time \[r(n)+T(m).\]
Now let's simplify the above when both $r(\cdot)$ and $T(\cdot)$ are some polynomial functions. Then since Step 1 takes at most $r(n)$ time and it computes $\mathbf{y}$, we must have that the size of $\mathbf{y}$ satisfies \[ m\le r(n).\] The the overall runtime is at most \[r(n)+T(r(n)).\] Note that under our assumption that $r(\cdot)$ and $T(\cdot)$ are some polynomial functions, the above runtime is $\text{poly}(n)$.
In other words, if $B$ can be solved in polynomial time, then the reduction $\mathcal{R}$ shows that $A$ can also be solved in polynomial time, i.e $A\le_P B$.
Note that in class, we have used the "contra-positive" implication: i.e. if $A\le_P B$ and $A$ is not solvable in polynomial time, then $B$ cannot be solved in polynomial time either.
Hint
It might be useful to consider the complement graph of $G$ and figure out what a clique in $G$ looks like in its complement. (The complement of $G=(V,E)$ is the graph $H=(V,E')$, where $(u,u)\in E'$ if and only if $(u,v)\not\in E$: i.e. if an edge is present in $G$, then it not present in $H$ and if an edge is not present in $G$, then it is present in $H$.)
Homework 8, Question 2
The problem
Given a graph $G$, output a largest clique of $G$, i.e., the output $S$ should be a clique and it must be the case that $G$ does not have a clique of size $|S|+1$.
Sample Input/Output pairs
- Input: $G_0$ (from Question 1)
- Output: The set of blue vertices.
Solving MaxClique solves the Clique problem
We note that there is a simple polynomial-time reduction from the Clique problem to the max clique problem:
- Given input $(G,k)$ for the Clique problem, run the algorithm for the MaxClique problem on $G$ to get output $S$.
- Output
true(for the Clique problem) if and only if $|S|\ge k$.
What Question 2 does is to show that there is also a polynomial time reduction in the other direction: i.e. there is a polynomial time reduction from the MaxClique problem to the Clique problem.
Question 2, part (a)
The main algorithmic ideas needed to solve both sub-parts is already there in the book: see the description at the bottom on Page 454 for how to solve similar problem for the independent set problem.
Sub-part (1)
Even though it is not needed, we provide the algorithm details of the reduction (we use A to denote the algorithm that solves the Clique problem in $T(n)$ time.
Algorithm Details
k = 1
for k in 2 .. n:
if not A(G,k): # This is the first value for which there is no clique of size k
return k-1 # Note that by definition there is a clique of size k-1
return n
Sub-part (2)
As stated in the book, you need to use binary search to figure out the size of the largest clique in $G$. However to get full credit for this sub-part, you need to specify the following:
Exercise
For what values of $k$ do you call A(G,k)? In particular, in binary search you rule out half of the possibilities-- how do you do that in this case?
Question 2, part (b)
The problem
Assume that the Clique problem from Question 1 is in $\mathcal{P}$. Show that then the MaxClique problem is also in $\mathcal{P}$ (i.e. there exists a polynomial time algorithm to solve the MaxClique problem).
We re-state the hint from the problem statement:
Hint
Note that since Clique is in $\mathcal{P}$, there exists a polynomial time algorithm $\mathcal{A}$ to solve that problem. Think of how you can call $\mathcal{A}$ multiple times to solve the MaxClique problem.
Satisfiability and SAT solvers
For Homework 8, Question 3, y'all will need to work with SAT solvers. In the remainder of the recitation, we will do the following:
Support page for SAT solvers
Review the support page on Satisfiability and SAT solvers.