Recitation 3
Recitation notes for the week of September 10, 2025.
Homework reminders
Here are some gentle reminders about HW policies:
- Make sure you submit your HW as a PDF only. Otherwise your submission will not be graded.
- Remember to put collaborators and sources in your submission file. Using
noneis also appropriate. - You can only collaborate with 2 other people and the collaboration must be for entire homework.
- Proof Idea and Proof Details must be clearly separated and labeled. Not doing so will result in a ZERO for the problem.
Stable Matching Review
The problem
Input:
- Set of $n$ men $M = \{m_1, m_2, \dots,m_n\}$
- Set of $n$ women $W = \{w_1, w_2, \dots, w_n\}$
- For every $m\in M$, $L_m$ a total ranking of all women
- For every $w\in W$, $L_w$ a total ranking of all men
Output: A stable matching.
Stable Matching
A perfect matching that has no instabilities.
Perfect Matching
For every $m\in M$, $m$ is assigned exactly $1$ woman AND for every $w\in W$, $w$ is assigned exactly $1$ man.
Instability
Given two pairs $(m, w)$ and $(m', w')$, where $m$ prefers $w'$ to $w$ and $w'$ prefers $m$ to $m'$ the pair $(m, w')$ is an instability.
Exercise 0
(This is to make sure you remember how to propagate negations in first order logic statements). How would you define a perfect matching to be a stable matching, directly in terms of the preferences (i.e. state logically what no instability means).
Perfect matching $\neq$ Stable matching
In a perfect matching we do not care about preferences, just that every individual has a match
Example 0
Consider the case of $n=3$, i.e. $W=\{w_1, w_2, w_3\}$ and $M=\{m_1,m_2,m_3\}$. In this case an example of a perfect matching will be $\{(m_1, w_1), (m_2, w_2), (m_3, w_3)\}$.
Note that $m_1$ can be with $3$ women, (given $m_1$'s assignment) $m_2$ with $2$, and (given $m_1$ and $m_2$'s assignment) $m_3$ with the last woman. I.e. we have $3\times 2\times 1 = 3!$ choices.
Homework 1 Q3: Finding all stable matchings
Remember
Gale-Shapley is only helpful for finding one stable matching (two if different depending on if women propose and if men propose) but not all of them.
Example 1
To illustrate the above comment, consider the following instance of the Stable Matching Problem: \[L_{m_1}: w_1 > w_2 > w_3 ~~~~ L_{w_1}: m_2 > m_3 > m_1\] \[L_{m_2}: w_2 > w_3 > w_1 ~~~~ L_{w_2}: m_3 > m_1 > m_2\] \[L_{m_3}: w_3 > w_1 > w_2 ~~~~ L_{w_3}: m_1 > m_2 > m_3\]
It can be verified that the following three are indeed stable matchings for the above instance: \[\{(m_1,w_1),(m_2,w_2),(m_3,w_3)\}\] \[\{(m_2,w_1),(m_3,w_2),(m_1,w_3)\}\] \[\{(m_1,w_2),(m_2,w_3),(m_3,w_1)\}\] In the above, the last one will not be discovered by the Gale-Shapley algorithm (irrespective of whether it is the women or the men doing all the proposing).
What do we need to do to find all stable matchings?
As is the case many times, it is good to go back to the definition:
Stable matching definition
A stable matching is a perfect matching with no instabilities.
Brute Force Algorithm (Algorithm Idea)
- Find all perfect matchings.
- Check if any perfect matching has no instabilities
Step 1: Find all perfect matchings
All perfect matchings can be found based off of the permutations of a set of $n$ elements. (We proved in last week's homework that the total number of perfect matchings is $n!$).
Example 2
Consider the set $\{m_1, m_2, m_3\}$.
There are six possible permutations: \[m_1~~ m_2~~ m_3\] \[m_1~~ m_3~~ m_2\] \[m_2~~ m_1~~ m_3\] \[m_2~~ m_3~~ m_1\] \[m_3~~ m_1~~ m_2\] \[m_3~~ m_2~~ m_1\]
But what about the women?
By keeping the women in numerical order, you are creating a different matching every time. Hence why the the total number of perfect matchings is just $n!$.
Step 2: Check for instability
Recall that we have an instability any time there is a pairing $(m,w)$ and $(m',w')$ such that $m$ prefers $w'$ to $w$ and $w'$ prefers $m$ to $m'$. In other words, there is at least one pair of couples where the man from Couple 1 and the woman from Couple 2 (or vice versa) prefer each other to their current spouses.
Your job
Figure out how to turn this information into a somewhat efficient algorithm and implement it.
HW 1 Question 1
Problem Statement
- There are two companies, $A$ and $B$
- $A$ and $B$ both have schedules $S_A$ and $S_B$
- Schedule $S_A$ holds shows $S_A[0] ... S_A[n-1]$ and likewise for $B$, where $S_A[i]$ (or $S_B[i]$) is a specific show owned by that company
- All the shows have ratings $r$ greater than $0$
The point of the schedules is to create matchups between shows from each company. The show at a specific time slot (index) in the schedule with the higher rating “wins” the match-up (if the ratings are tied, assume company $A$ wins the match-up). The companies are trying to win as many match-ups as possible.
Our goal is to determine if there is a pair of schedules that are stable.
We define a stable match-up to be a pair of schedules where neither company can change their schedule to win more match-ups. For example, company $A$ has shows two shows ($S_A[0]$ and $S_A[1]$) with ratings $10$ and $9$ and company $B$ has shows with ratings $8$ and $6$.
An example schedule match-up:
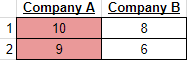
The numbers in the cells represent the ratings of the shows (since each show has a unique rating). Highlighted in pink are the winning shows.
In this case, we see $S_A[0]$ and $S_B[0]$ are matched against each other, and $S_A[1]$ and $S_B[1]$ are matched against each other. This particular match-up is a stable match-up, because neither company can change their schedule to win more match-ups. For example, if we changed the order of $B$’s shows, we would get:
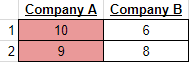
And in this schedule, $A$ still wins both matchups.
What if instead of $9$, company $A$’s second show has a rating of $7$? If we keep the same show schedule, then the matchups become:
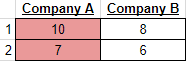
Right now, $A$ still wins both match-ups, but if $B$ were to switch its schedule so that the match-ups were:
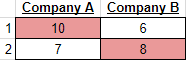
Now $A$ only wins one matchup, and $B$ also wins one. This means the original match-up was not stable, since $B$ managed to win more match-ups by changing their schedule. Furthermore, $A$ could then react back and change their schedule to also be flipped, and win both match-ups again.
Part (a)
Problem Statement
Let’s look at a pair of show line-ups such that the lowest rated show for company $A$ is still a higher rating than the highest rated show for company $B$. What can we say about the stability of all of the match-ups? Can we say that given the input as described above, all schedules are stable? What would we need in order to say this?
Proof Idea
Well, we know that the minimum rated $A$ show is still greater than the maximum rated $B$ show, so we could say that in any match-up in this scenario, $A$ would come out winning every match-up.
Lemma
If the lowest rated $A$ show is greater than the highest rated $B$ show, then in all possible schedules, $A$ wins all slots.
If this lemma is true (proving it is your job), then we know that no matter the schedule $B$ makes for its shows, $A$ will win all match-ups, making the schedule of match-ups stable.
Proof Details
If the lemma is true, then we know that in this problem, $A$ will always win all match-ups. If $A$ always wins all match-ups, then no change could be made to the schedule of company $B$ to make them win more match-ups (in fact, they will always have zero wins). This would mean that all schedules are stable, since $A$ cannot win more than the number of match-ups, and $B$ cannot alter their schedule in any meaningful way.
Exercise
Finish this proof by proving the lemma above to be true.
Part (b)
For this problem, you have to first decide whether the statement is always true. See the walkthrough video for Q1 for formal first order logic statement of what proving the statement to be true or false means (also repeated below).
If your answer is True
If your answer is true then you need to argue the following: \[\forall n>0, \forall \text{ show ratings }, \exists (S,T) \text{ for which the following holds (i) } \forall S'\ne S, (S',T) \text{ has no more wins for } A \text{ than } (S,T) \text { AND (ii) } \forall T'\ne T, (S,T') \text{ has no more wins for } B \text{ than } (S,T)\]
While you could argue the above without giving an algorithm, to get credit for this problem (if the general statement is true) is to given an algorithm that on any possible input gives a stable pair of schedules. Note that when we argued for the stable matching problem, every possible input has a stable matching, we proved this result by presenting an algorithm (the Gale-Shapley algorithm) that on every possible input, outputs a stable matching-- so if the general statement is true you have to prove it to be true by presenting an algorithm for the new problem in Q1.
If your answer is False
If your answer is false then you need to argue the following (note that the the logical statement below follows by using standard rules for negating a first order logical statement ): \[\exists n>0, \exists \text{ show ratings }, \forall (S,T) \text{ the following holds (i) } \exists S'\ne S, (S',T) \text{ has strictly more wins for } A \text{ than } (S,T) \text { OR (ii) } \exists T'\ne T, (S,T') \text{ has strictly more wins for } B \text{ than } (S,T)\]
In other words, if your answer is false, what you're saying is that it is possible that on some inputs of shows and ratings for each company, there is no stable schedule. What would this require? Remember, an unstable schedule $(S,T)$ is one where either company can change their schedule to create a different set of match-ups where that company then wins more of the match-ups than before. However, showing that one specific schedule $(S,T)$ is unstable does not mean that all possible schedules are unstable. (In other words, showing a specific schedule $(S,T)$ is unstable does not rule out the possibility that there can exist another schedule $(S',T')$ that is stable). However, to show that the statement is false, we need to show that ALL schedules are unstable. If all schedules are unstable, that means that no matter which schedule is picked, there is always a way for one of the companies to change their schedule to have strictly more wins. You need to describe an input that follows this behavior across all schedules of match-ups.
HW 1 Question 2
Previously we have looked at specific examples when discussing inputs for algorithms. A different way to consider the input is in terms of a family of examples. The difference between a specific example and a family is that a family represents many examples all at once, usually by having some rules on how to construct new examples as the input size grows. Families are generally used to show a trend or property in the algorithm or in the family of inputs.
Part (a)
Let us consider a family of inputs for the stable matching problem that allows for $\Omega(n)$ stable matchings. This means that for any input size, the list of men, women, and their preference lists create at least $cn$ different stable matches ($c$ is a constant, but gets simplified when talking about asymptotic complexity).
First, let’s look at two ways to represent a family of inputs:
Explicit/Algorithmic
This way involves just explaining what the family is in plain words or algorithmically, like pseudo-code.
For our problem, our family has two groups, $M$ (men) and $W$ (women), each containing $m_i$ and $w_i$ such that $0 < i ≤ n$ and each m and w have preference lists as follows:
Men
- $m_1: w_1 > w_2 > ... > w_{n-1} > w_n$
- $m_2: w_2 > w_3 > ... > w_{n} > w_1$
- $...$
- $m_n: w_n > w_1 > ... > w_{n-2} > w_{n-1}$
Women
- $w_1: m_2 > m_3 > ... > m_n > m_1$
- $w_2: m_3 > m_4 > ... > m_1 > m_2$
- $...$
- $w_n: m_1 > m_2 > ... > m_{n-1} > m_n$
Functional
Same as before, we have $M$, $W$, $m_i$, $w_i$, and $i$ such that $0<i≤n$.
For men, we show:
$L_{m_1} = w_1 > w_2 > ... > w_n$
$L_{m_{i+1}} = L_{m_i}$ shifted one left (with wraparound). That is, the same as $L_{m_i}$, but with the first woman moved to the end.
For women we show:
$L_{w_1} = m_2 > m_3 > ... > m_n > m_1$
$L_{w_{i+1}} = L_{w_i}$ shifted one left (with wraparound).
We could also show an inductive definition of the family, but this does not work very well for this particular case.
As an exercise:
Compare the two representations, and verify that they convey the same information.
Now with this family, we want to show there are at least $n$ stable matchings. So how can we prove that this family satisfies this? Well this is where working with a family of inputs helps, as we can find some property of this input that is repeatable and helps prove there are at least $n$ stable matches. In this case, we will help prove this by outlining a lemma (which you will then prove for your proof of correctness).
Proof Idea
Let’s say that for our stable matching, let’s consider an input of size $4$ ($n=4$). This gives us preference lists as follows:
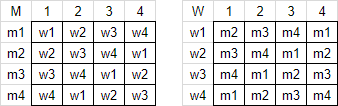
In these charts, the person whose preference list we are referencing is noted on the left side, followed by their preference list in order of most preferred to least preferred.
One stable matching we can consider is if all of the men get their most preferred choice. Looking at the preference lists as a grid, we notice that matching each man with their most preferred choice means all of their matches are in column $1$, and the corresponding matches for the women are in column $4$.
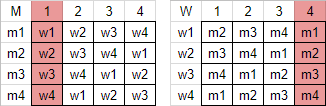
This is the other way around if the women get their most preferred choices $-$ their choices are in their column $1$, and the men’s are in column $4$.
Now imagine the men all get their second most preferred woman. That is, $m_1$ to $w_2$, $m_2$ to $w_3$, etc. This puts all of their matches in column $2$ in their lists, and in the women’s list, the men are all in column $3$.
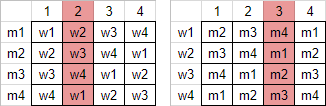
We can expand this further if we would like, but we are already noticing a trend. That is, for a given stable matching, the matches represent some column i in one list, and column $n-i+1$ in the other. We can present this as a lemma:
Lemma
If you match one group with their preferences in a specific column $i$, then the other group is matched with their preferences in column $n-i+1$.
Using this lemma, we can quickly create $4$ different potential stable matchings:
- $(m_1,w_1),(m_2,w_2),(m_3,w_3),(m_4,w_4)$
- $(m_1,w_2),(m_2,w_3),(m_3,w_4),(m_4,w_1)$
- $(m_1,w_3),(m_2,w_4),(m_3,w_1),(m_4,w_2)$
- $(m_1,w_4),(m_2,w_1),(m_3,w_2),(m_4,w_3)$
These are all stable, since no man prefers a woman who has that man higher on her preference list than her current match, and vice versa for the women.
If this lemma is true (you must prove it yourself), then we can say that there are at least $n$ stable matchings, which is $\Omega(n)$ stable matchings.
Proof Details
If the given lemma is true, then we can generate n matchings by going through the preference lists column by column. These matchings are stable since no man prefers a woman who has that man higher on her preference list than her current match, and vice versa for the women. For example, if we match each man to their second most preferred woman, then we get:
- $(m_1,w_2),(m_2,w_3),(m_3,w_4),(m_4,w_1)$
For $m_1$, his only more preferred woman is $w_1$. She is matched to $m_4$, and would prefer either $m_2$ or $m_3$ to this match, but NOT $m_1$, as he is ranked lower than $m_4$, her current match. This holds for the other $3$ men as well, as well as for each man should we match them to a different column.
We can then say that there are n stable matchings, which is $\Omega(n)$ stable matchings.
Your job will be to:
Finish this proof by proving the above lemma.
Note
Note that this lemma is for this one given family of inputs, and (probably) will not work for others.
Part (b)
Now we need to find a family that produces $\exp(n)$ matches (exponentially many). While using the family we used in part (a) is not advised, it is important to note the things we learned. We noticed something structurally about our input, that is, something repeating that holds regardless of the size of the input. Finding some property about the structure of the input makes it easy to use structural induction due to the repeating nature of the property. It also might help you to think of the way the family looks visually -- draw a picture and see if there’s something similar to note like we had with the columns lemma for part (a).
Example Proof: Chapter 1 Ex. 1
Exercise 1
Decide whether the following is true or false. If true, prove it. If it is false, give a counterexample.
In every instance of the Stable Matching Problem, there is a stable matching containing a pair $(m,w)$ such that $m$ is ranked first on the preference list of $w$ and $w$ is ranked first on the preference list of $m$.
Proof Idea
False.
In order to prove this statement, it is sufficient to provide a counterexample to the statement above. We will show that there is an instance of the stable matching problem that does not contain the pair $(m,w)$ where $m$ is ranked first on the preference list of $w$ and $w$ is ranked first on the preference list of $m$.
Proof Details
The example below is an instance of the stable matching problem since there are $n=2$ men and $n$ women where every $m\in M$ and every $w\in W$ has a preference list of $n$ women and men, respectively. \[L_{m_1} = w_2 > w_1~~~~ L_{w_1} = m_1 > m_2\] \[L_{m_2} = w_1 > w_2~~~~ L_{w_2} = m_2 > m_1\]
There are only 2 possible matchings and only 2 stable matchings for this instance of the stable matching problem \[\{(m_1,w_2), (m_2,w_1)\}\] and \[\{(m_1,w_1), (m_2,w_2)\}\].
A pair such that both partners rank their partner first does not exist for this problem.
Pigeon Hole Principle
The principle
Consider any assignment of $n +1$ pigeons to $n$ holes. Then there exists at least one hole with at least 2 pigeons in it.
Example 3
There are 500 students in a school. By pigeonhole principle, there must be at least 2 students that share a birthday.
For more
For the proof, more examples, and variations of the principle see the support page on the pigeonhole principle.
Further Reading
- Make sure you carefully read the policy documents: Syllabus and Homework policies.
- Support page on pigeonhole principle.
- Notation for the stable matching problem.