Recitation 7
Recitation notes for the week of October 8, 2025.
This recitation, we will essentially go over the material from the project page. The material on Problem 1 and Problem 2 are just copied over from the project page. The discussion on reflection problem 1 is also mostly copied over from the reflections page, though there is some new material here.
Reminders
There are quite a few moving parts in the project, and it is easy to forget the numerous reminders and suggestions, so we collect those here again for your reference.
Groups should agree on one programming language
While the submissions for the coding problems in this project can be done in C++, Java or Python like in the Question 3s on the homework, we highly recommend that the group agrees on one programming language for the group. This will make it much easier for your group to make progress and collaborate.
The same group for ALL problems
You are expected to work in the same group for ALL problems in the coding project. Not doing so will be considered to be an academic integrity violation. We will use the groups y'all register on Autolab as part of your Autolab Project Group Registration submission for your project submissions.
There is ONE exception to the above rule: It is OK if the group becomes smaller (e.g. if a group member resigns) but in that case another student cannot be added to group. If you need clarification on this, please get in touch with Atri.
There are no optimal algorithms known!
Other than the first problem, we do not know of optimal algorithms to solve the rest of the problems and we suspect that doing so is not possible (definitely not within a semester.) Note that this is unlike the HW Q3s where your code is supposed to always output the optimal/correct solution; that is to say, you will have to think of algorithms where you might not be able to prove any guarantee on how good your output is.
Start early!
There is a reason we are giving y'all about two months to do this project. If your group starts even the week before the project is due, your group will be in trouble especially beyond the first problem. Also for most problems you will have to think of algorithms beyond what we cover in class, so the more time your spend on this, the better.
What algorithms techniques will be relevant?
Our solutions only use algorithmic techniques (plus some heuristics) that we will cover in class. However, it is entirely possible that other algorithmic techniques might be useful. One such technique that we will not cover in class is that of network flows (Chapter 7 in the textbook). However, again to emphasize since we have not used any concepts from that chapter in our solutions, we can speak to the efficacy of such techniques for this project. In other words, if your group decides to use network flow in your submission and it does not work well, then that is on your group.
Optimizing the runtime of your code is NOT the main objective
Unlike the HW Q3s, there will be no timeouts for individual inputs (though there will be a timeout per submission). This is because unlike the HW Q3s, the main goal in this coding project submissions will be to generate as much "revenue" as possible (read on for more details on this)-- optimizing the runtime would/should be a secondary objective, but again, there is an overall timeout so really inefficient implementations (and definitely non-polynomial runtime algorithms) will not make the cut.
Problem 1
Input
You are given ForProfitOnly's communication graph $G = (V,E)$, the content provider node $i$, a set of clients $C\subseteq V \setminus \{i\}$, bandwidth size $b_u$ for every router $u$, and for all clients you are given their tolerance threshold, the payment they make, and their priorities (which are set to a default value). In summary, following is the input:
- $G = (V, E)$
- $i \in V$
- $C$ s.t. $C \subseteq V \setminus \{i\}$
- For all $u \in V \setminus \{i\}$, $b_u$ s.t. $b_u = \infty$
- For all $c \in C$, $\alpha_c$ s.t. $\alpha_c = 1$
- For all $c \in C$, $\text{priority(c)} =$ PRIORITY_DEFAULT
Penalty
The notion of penalty for this problem is the revenue loss that ForProfitOnly has to face. In this problem, it is possible to lose money only if some clients unsubscribe from ForProfitOnly due to its poor service (slow internet). A client $c \in C$ may unsubscribe from ForProfitOnly if $c$'s internet is slow enough to "beat" $c$'s tolerance threshold $\alpha_c$.
More precisely, let $P'_c$ be the $i-c$ path generated by your algorithm to route packets from $i$ to $c$. Then if $D(P'_c)$ exceeds $\alpha_c \cdot d(c)$, then $c$ unsubscribes from ForProfitOnly, and ForProfitOnly does not receive $c$'s payment $\text{pmt}_c$. This causes a drop in ForProfitOnly's revenue. Thus, the penalty that ForProfitOnly faces from client $c$ is either $\text{pmt}_c$ or nothing (which is 0). This calculation is done by the $pen_0$ function for each client $c \in C$. Below is a formal description of penalty function:
- $pen_0(c, D(P'_c),\alpha_c, d(c),\text{pmt}_c)$ is the penalty function that accounts for the client/revenue loss that
ForProfitOnlyfaces due to client $c \in C$. $pen_0$ has five inputs:- client $c \in C$
- $D(P'_c)$ which is the total delay of $i-c$ path generated by your algorithm
- $\alpha_c$ which is the tolerance of client $c$
- $d(c)$ which is the minimum delay of any $i-c$ path
- $\text{pmt}_c$ for $c \in C$
If $D(P'_c) > \alpha_c \cdot d(c)$, then client $c$ unsubscribes from ForProfitOnly(and subscribes to some other ISP or say uses their cell phone as a way of connecting to the internet). So you lose their portion of the revenue. Otherwise, $pen_0(c,D(P'_c),\alpha_c,d(c),\text{pmt}_c)$ outputs $0$.
Thus, for this problem, $pen_0(c,D(P'_c),\alpha_c,d(c),\text{pmt}_c) = \begin{cases} \text{pmt}_c &\text{if} \quad D(P'_c) >\alpha_c \cdot d(c) \\ 0 &\text{ otherwise} \end{cases}$
Revenue
ForProfitOnly receives a payment $\text{pmt}_c$ from every client $c \in C$ unless $c$ has unsubscribed from ForProfitOnly's services. This means that ForProfitOnly receives nothing or a $0$ payment from any client $c$ who has unsubscribed from its services. Thus, we can define revenue from client $c$ as the payment received from $c$ minus the penalty faced due to $c$. This is calculation is done by the $rev$ function for each client $c \in C$. Below is a formal description of $rev$ function:
- Let $rev(c, D(P'_c),\alpha_c,d(c),\text{pmt}_c)$ be the revenue received from client $c$. Here, $rev(c, D(P'_c),\alpha_c,d(c),\text{pmt}_c) = \text{pmt}_c - pen_0(c,D(P'_c),\alpha_c,d(c),\text{pmt}_c)$
Now that we defined revenue for each $c \in C$, we define total revenue to be the sum of the revenue received from each $c \in C$.
- Thus, total revenue = $\sum_{c\in C} rev(c,D(P'_c),\alpha_c,d(c),\text{pmt}_c)$
Output
You need to come up with an algorithm that generates one $i-c$ path to route packets from $i$ to $c$, for each $c \in C$. You should output a list of $i-c$ paths for all $c \in C$. There can be multiple $i-c$ paths from $i$ to $c$, but your algorithm should generate an $i-c$ path that contributes towards satisfying the objective (see below) for this problem. To put it formally, you need to output:
- $L_{P'}$ which is a list of $P'_c$ for all $c \in C$
Objective
Maximize total revenue (over all possible choices of $i-c$ paths for each $c\in C$).
Hint
The optimal solution for this problem is very closely related to a homework problem that y'all have already seen in this course.
Example 1
A Solution
If the graph $G$ for this problem is our graph from Example 0, then here is a valid output (see the figure below):
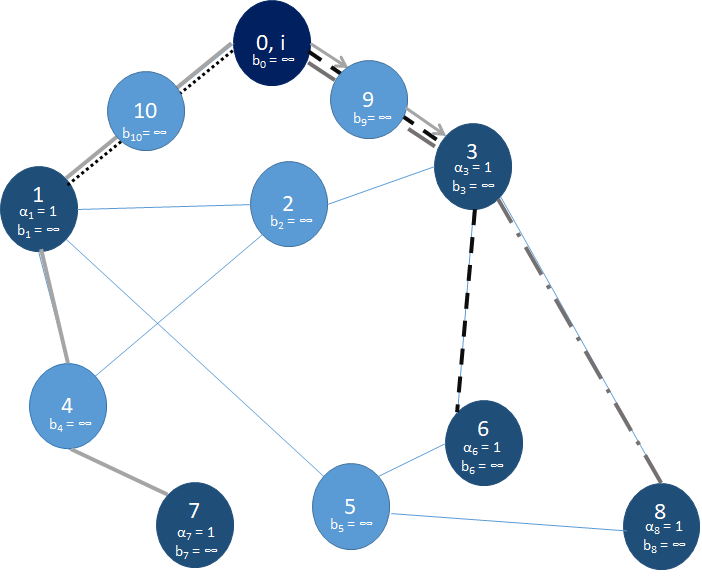
That is, the output $L_{P'} = [P'_1,P'_3,P'_6,P'_7,P'_8]$. Where, $P'_1 = [0,10,1], P'_3 = [0,9,3], P'_6 = [0,9,3,6], P'_7 = [0,10,1,4,7], P'_8 = [0,9,3,8]$.
Since each $b_c = \infty$ ,for $c \in \{1,3,6,7,8\}$, the optimal routing protocol will incur a delay $d(c)$ for each $c$. This is because for each path P’_c, we will have $D(P'_c) = d(c)$ (see below for bit more details). Thus, for all $c \in C$, $pen_0(c) = 0$ because $D(P'_c) = d(c)$. So $rev(c) = \text{pmt}_c$, and thus total revenue would simply be the sum of payments from each client.
Justification for claim on revenue
Since all $b_c = \infty$, the routing protocol will incur a delay of $d(c)$. This is because for each path $P’_c$, we will have $D(P’_c)$ is the number of edges in $P'_c$ and further, for each $P’_c$ above, this is also $d(c)$. Thus, in this case we have $pen_0(c) = 0$. For example, we have $d(1)=2$, which is also the number of edges in $P'_2$: i.e. $D(P’_1) = 2$. Since $d(1)$ is the shortest possible delay we have found an optimal solution for path $P'_1$ and experience no penalty. A similar argument works for the rest of the clients.
Note that:
- $D(P’_1) = 2 = d(1) $
- $D(P’_3) = 2 = d(3) $
- $D(P’_6) = 3 = d(6) $
- $D(P’_7) = 4 = d(7) $
- $D(P’_8) = 3 = d(8) $
So, total revenue $= \$30+ \$40 + \$35 + \$40 + \$45 = \$190$, which is the maximum possible revenue.
Reflection Problem 1
Important reminders about reflection questions
There is no "right" or "wrong" answer
Perhaps the biggest difference from other CSE 331 questions (both programming and proof based questions) is that pretty no much no answer is "right" or "wrong" in any absolute sense. Y'all will notice that for some of the questions, the answer might depend on some of the assumptions you make--and in many cases the answer would really depend on who is answering the question. While ambiguity might feel a bit disquieting, the ambiguity is inherent for these kinds of questions, so embrace the ambiguity!
More specifically, do not waste your time trying to figure out what I am expecting from an answer-- because I do not have any set answer that I'm looking for! What I am interested is in hearing your group's thoughts on the questions. In particular, even if I disagree with your justification, that does NOT mean you will get penalized. Again there is no "right" or "wrong" answer!
The justifications do not have to be long
While it might seem like there are a lot of questions, please note that we are not expecting really long details justifications. In most cases a couple of sentences or a paragraph would suffice. To give a sense of the amount of detail expected, think of the level of detail to be on the lines of what is expected of y'all in a proof idea. So we only want to read about the main ideas behind your justification.
A useful resource
For the specific reflection questions, we will be quoting from Cathy O'Neil and Hanna Gunn's book chapter titled Near-Term Artificial Intelligence and the Ethical Matrix .
You can access the book chapter as a PDF from UB Libraries .
While the book is about ethical issues in AI, the concepts in the specific chapter are applicable more widely and in particular, for our project (that does not have anything to do with AI).
The actual questions
This question is a bit different
Unlike the questions for other problems, for Problem 1, the question is related to the project as a whole (and is not really related to the first coding problem). So please make sure you at least read all the problem statements before attempting this question.
Who/What are stakeholders?
In this question, you will have to identify stakeholders in the projects (i.e. think of all the five problems) when answering this question. Roughly speaking a stakeholder is an entity (could be individuals or a collection of individuals) who have some "stake" in a setup/company (in this case think of stakeholders in the entire setup of the project): this could be some obvious ones like customers of a company or it could be more subtle e.g. a governmental agency that regulates an industry for example.
Your Task
Cathy O’Neil and Hanna Gunn’s ethical matrix for algorithm design begins with a simple question: Does my algorithm work? However, algorithms do not “work” in a vacuum. So, this question becomes more complicated when we also ask: Whom does my algorithm work for?
Below, we’ve provided five entities that are interested in how well your algorithm works for them. These are your stakeholders. For reference, stakeholders are those who have a unique “stake” in an enterprise. They are the groups of people interested in and affected by the work your algorithm will do. Each stakeholder group in your list must have their own unique set of interests or concerns. For example, you could not list two stakeholders who are only concerned with “profit” because they would be considered the same group as they have the same stake. Your task is to list the stakes for these five stakeholders in your routing algorithm. This will require you to imagine the needs of these stakeholders and the concerns they might have about how your design works.
Listed below are five entities. In your submission, for each entity:
- List the stakes for these five stakeholders in the project setup.
Stakeholder 1 (2 point)
Stakeholder 2 (2 point)
Stakeholder 3 (2 point)
Local/state legal system.
Stakeholder 4 (2 point)
Internet customers in rural areas.
Stakeholder 5 (2 point)
Internet customers in urban areas.
Preliminary Grading Guidelines
Below is a preliminary instantiation of the generic grading rubric above for (all ten parts of) Problem 1. In actual grading, we will use a grading rubric that expands on the preliminary grading rubric below.
- Level 0
- The authors did not respond with all 10 stakes; OR
- Answers may not be entirely relevant to the assignment.
- Level 1
- The authors did respond with all 10 stakes. Although, the responses may be underdeveloped; AND
- The authors clearly understand the questions, but have not demonstrated much effort in thinking through the different interests each stakeholder would have. Answers may seem perfunctory.
- Level 2
- The authors respond with all 10 stakes thoroughly and thoughtfully; AND
- The authors clearly demonstrate their grasp of the questions and the various perspectives each stakeholder might have on the same design; AND
- They demonstrate that what stakeholders’ value differs depending on their own context.
A sample solution
To get y'all started in reflection questions as well as give a sense for how the preliminary rubric would be applied, we present three solutions corresponding to three levels for Stakeholder 5:
Stakeholder 1 (2 point)
Level 0 solution
From the Federal Communications Commission website (FCC) : The Federal Communications Commission regulates interstate and international communications by radio, television, wire, satellite, and cable in all 50 states, the District of Columbia and U.S. territories. An independent U.S. government agency overseen by Congress, the Commission is the federal agency responsible for implementing and enforcing America’s communications law and regulations.
The above solution is level 0 since the above does not have anything to do with the specific project you are working on as am employee of ForProfitOnly.
Level 1 solution
FCC is related to Problem 3 on the project.
The above solution is level 1 since the answer connects FCC to the specific part of the project but with essentially no detail on what their "stake" is in the specific project you are working on as am employee of ForProfitOnly.
Level 2 solution
In Problem 3 in our project, the routing algorithm we develop to route packets would be of interest to FCC since they will be testing the quality of service/Internet speed at certain nodes to make sure ForProfitOnly is delivering the promised speed. I.e. the FCC's stake is carrying out its mission and make sure ForProfitOnly is delivering on the promised Internet speed in the specific subset of clients $S$ in the problem 3 definition.
The above solution is level 2 since not only the answer connects FCC to the specific part of the project but clearly state the "stake" of FCC and why they might be interested in the algorithm developed by your group. Further it explicitly connects to specific part of the input in problem 3 that is relevant to FCC. (Note: You might not be able to do the latter with all the stakeholders.)
Common Mistake
A common mistake for this problem is to not pay attention to the following part of the rubric for level 2: They demonstrate that what stakeholders’ value differs depending on their own context. In other words, the stake of each stakeholder must be unique to them-- or at the very least should not be something that applies equally well to any of the other nine stakeholders. Not doing so will result in a level 1 or below.
Problem 2
Input
The input for the problem is the same as the previous one except for the bandwidth being limited and the tolerance threshold for every client being an arbitrary value greater than or equal to $1$. To put it formally, following is the input:
- $G = (V, E)$
- $i \in V$
- $C$ s.t. $C \subseteq V \setminus \{i\}$
- For all $u \in V \setminus \{i\}$, $b_u$ s.t. $b_u < \infty$
- For all $c \in C$, $\alpha_c$ s.t. $\alpha_c \ge 1$
- For all $c \in C$, $\text{pmt}_c$
- For all $c \in C$, $\text{priority(c)} =$ PRIORITY_DEFAULT
Note
The highlighted input, is the part of the input that is different from the previous problem.
Output
Now given these real-world limitations, you should come up with an algorithm that generates $i-c$ paths for each client $c \in C$, in a way that contributes towards achieving the objective. Just like Problem 1, you should output a list of $i-c$ paths for all $c \in C$. That is, you need to output:
- $L_{P'}$ which is a list of $P'_c$'s for all $c \in C$
Objective
Same as Problem 1.
Example 2
A Solution
If the graph $G$ for this problem is our graph from Example 0, then here is a valid output:



Note
The $\alpha$ values given above will be used in the example graph for the remaining problems also (except for a small change to $\alpha_3$ in Problem 5).
That is, the output $L_{P'} = [P'_1,P'_3,P'_6,P'_7,P'_8]$. Where, $P'_1 = [0,10,1], P'_3 = [0,10,1,2,3], P'_6 = [0,10,1,5,6], P'_7 = [0,10,1,4,7], P'_8 = [0,9,3,8]$.
We will consider the paths given above to compute the penalties for each client. So for path $1$, $\alpha_1\cdot d(1)$ is $1 \cdot 2$, which is $2$. Next we compare that to our $D(P’_1)$, by finding the number of edges in each path and making sure that there is enough bandwidth to transfer packets each tick. If our $D(P’_c)$ is less than or equal to $\alpha_c\cdot d(c)$ value we receive no penalty. For notational convenience (in our worked out calculation below), if $D(P’_c) \leq \alpha_c \cdot d(c)$ we say “accept”, else “reject”.
Total Revenue
We claim that the revenue generated from the above solution is $\$155$ while the solution from Example 1 will generate a total revenue of $\$110$ for this input. See below for more details
Determining $D(P')$ for every client
We claim that: $D(P’_1) = 2, D(P’_3) = 4, D(P’_6) = 4, D(P’_7) = 4, D(P’_8) = 3$. We verify this by tracing each time step in the routing simulation:
At Time Tick $0$:
Current: All packets at 0.
Passed on: All
At Time Tick $1$:
Current:
- $\text{pkt}_1$ at node $10$
- $\text{pkt}_3$ at node $10$
- $\text{pkt}_6$ at node $10$
- $\text{pkt}_7$ at node $10$
- $\text{pkt}_8$ at node $9$
Passed on: All
At Time Tick $2$:
Current:
- $\text{pkt}_1$ at node $1$
- $\text{pkt}_3$ at node $1$
- $\text{pkt}_6$ at node $1$
- $\text{pkt}_7$ at node $1$
- $\text{pkt}_8$ at node $3$
Reached: $\text{pkt}_1$
Passed on: $\text{pkt}_3, \text{pkt}_6, \text{pkt}_7,\text{pkt}_8$
At Time Tick $3$:
Current:
- $\text{pkt}_3$ at node $2$
- $\text{pkt}_6$ at node $5$
- $\text{pkt}_7$ at node $4$
- $\text{pkt}_8$ at node $8$
Reached: $\text{pkt}_8$
Passed on: $\text{pkt}_3, \text{pkt}_6, \text{pkt}_7$
At Time Tick $4$:
Current:
- $\text{pkt}_3$ at node $3$
- $\text{pkt}_6$ at node $6$
- $\text{pkt}_7$ at node $7$
Reached: All packets have reached their destination so routing terminates.
Determining Penalty and Calculating total revenue
Now lets see what $pen_0$ function outputs for each client:
- $pen_0(1) = 0$
- $D(P’_1) = 2 , d(1) \cdot \alpha_1 = 2, 2 \leq 2$, so accept
- $pen_0(3) = 0$
- $D(P’_3) = 4 , d(3) \cdot \alpha_3 = 8, 4 \leq 8$, so accept
- $pen_0(6) = 35$
- $D(P’_6) = 4 , d(6) \cdot \alpha_6 = 3, 4 > 3$, so reject
- $pen_0(7) = 0$
- $D(P’_7) = 4 , d(7) \cdot \alpha_7 = 4, 4 \leq 4$, so accept
- $pen_0(8) = 0$
- $D(P’_8) = 3 , d(8) \cdot \alpha_8 = 3, 3 \leq 3$, so accept
Our total revenue is calculated by subtracting the summation of all penalties from our total possible revenue.
Total revenue $= 190 - 35 = 155$
Example 1 solution
The solution to Problem 1 is a worse solution for this problem. We will go through the calculations to see what total revenue generated by using Example 1's solution for this problem.
Solution to Example 1
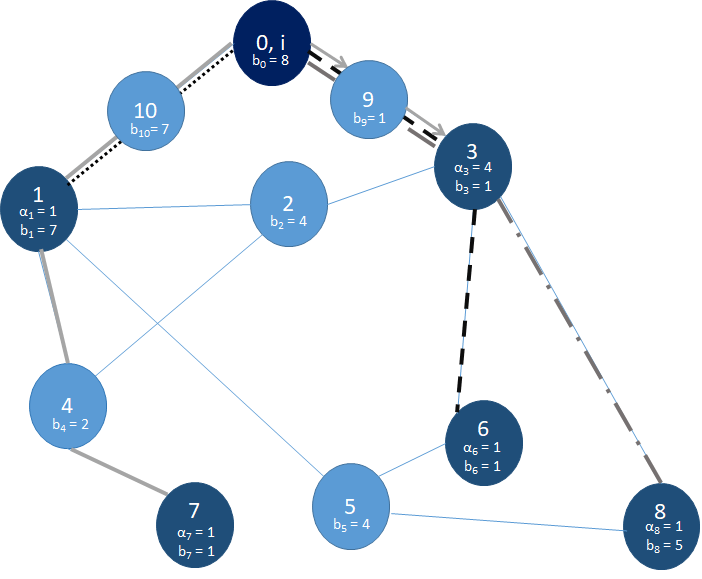


In the above picture we use Example 1's solution to solve this problem. Now we will see, why this solution is worse for this problem.
Determining $D(P')$ for every client
We claim that: $D(P’_1) = 2, D(P’_3) = 2, D(P’_6) =4, D(P’_7) = 4, D(P’_8) = 5$. Let's now trace each time tick in the routing simulation:
At Time Tick $0$:
Current: All packets at 0.
Passed on: All
At Time Tick $1$:
Current:
- $\text{pkt}_1$ at node $10$
- $\text{pkt}_3$ at node $9$
- $\text{pkt}_6$ at node $9$
- $\text{pkt}_7$ at node $10$
- $\text{pkt}_8$ at node $9$
Passed on: $\text{pkt}_1, \text{pkt}_3, \text{pkt}_7$
Delayed: $\text{pkt}_6, \text{pkt}_8$
At Time Tick $2$:
Current:
- $\text{pkt}_1$ at node $1$
- $\text{pkt}_3$ at node $3$
- $\text{pkt}_6$ at node $9$
- $\text{pkt}_7$ at node $1$
- $\text{pkt}_8$ at node $9$
Reached: $\text{pkt}_1, \text{pkt}_3$
Passed on: $\text{pkt}_6, \text{pkt}_7$
Delayed: $\text{pkt}_8$
At Time Tick $3$:
Current:
- $\text{pkt}_6$ at node $3$
- $\text{pkt}_7$ at node $4$
- $\text{pkt}_8$ at node $9$
Passed on: $\text{pkt}_6, \text{pkt}_7, \text{pkt}_8$
At Time Tick $4$:
Current:
- $\text{pkt}_6$ at node $6$
- $\text{pkt}_7$ at node $7$
- $\text{pkt}_8$ at node $3$
Reached: $\text{pkt}_6, \text{pkt}_7$
Passed on: $\text{pkt}_8$
At Time Tick $5$:
Current:
- $\text{pkt}_8$ at node $8$
Reached: $\text{pkt}_8$
NOTE: Some of the $D(P'_c)$ values have changed from the previous solution due to bandwidth restrictions.
Determining Penalty and Calculating total revenue
Now let us see what $pen_0$ function outputs for each client:
- $pen_0(1) = 0$
- $D(P’_1) = 2 , d(1) \cdot \alpha_1 = 2, 2 \leq 2$, so accept
- $pen_0(3) = 0$
- $D(P’_3) = 2 , d(3) \cdot \alpha_3 = 8, 2 \leq 8$, so accept
- $pen_0(6) = 35$
- $D(P’_6) = 4 , d(6) \cdot \alpha_6 = 3, 4 > 3$, so reject
- $pen_0(7) = 0$
- $D(P’_7) = 4 , d(7) \cdot \alpha_7 = 4, 4 \leq 4$, so accept
- $pen_0(8) = 45$
- $D(P’_8) = 5 , d(8) \cdot \alpha_8 = 3, 5 > 3$, so reject
So the total revenue $ = \$190 - (\$35 + \$45) = \$110$. Hence, this is definitely worse than the previous solution for this problem.