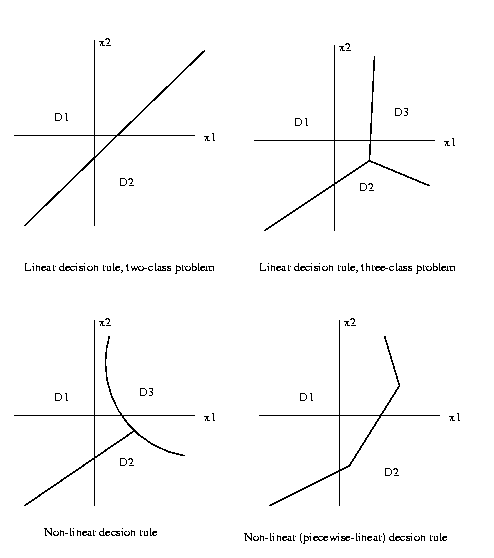
Chapter 7: Object Recognition
Some computer vision applications require no more than
the successful implementation of steps
discussed so far.
Eg: Count the number of blobs of size >10
pixels.
Eg: Determine if the single object in the image (a gear
imaged on a conveyer belt) has the correct number of
teeth.
But these are only the simplest of computer vision
applications. The majority requires more than mensuration,
the quantitative measurement of scene
attributes.
Typically we need to recognize or classify the objects in
the scene. This requires more than the ability to segment
and then characterize shape of each candidate object in
the scene, it also requires domain knowledge.
Questions that cannot be answered without domain
knowledge:
1. What kind of objects
are
we looking for?
2. What are the defining characteristics of these
objects?
3. How may instances of these objects vary from some
ideal
instance (eg. size, pose, lighting)?
This procedure is referred to as object recognition (OR). It
brings together shape representations derived from the
image with data structures and algorithms which represent
object classes and methods for matching. These may be
pre-selected and unchanging, or they may be modified as
the system operates. If this modification results in
performance enchancement, this process is
called learning.
Knowlege representation
Since we propose to combine domain knowledge with
generic image analysis data, we need to know how
this domain knowledge is to be represented. There
are many forms which can be used to represent
knowledge:
1. Vectors of scalar parameters;
2. Probability density and mass functions;
3. Set of IF-THEN rules;
4. Graphs and nets (semantic and neural;
5. Predicate logic, fuzzy
logic, other logics.
Specific methods of knowledge representation make most
sense within the context of the methods of object rec-
ognition that use them. So we will proceed to develop
the principles of several alternative approaches to
object recognition.
In general, there are two broad approaches to object
recognition, by analysis and by synthesis.
OR by analysis: describe each candidate object by
a vector of pre-determined features. Decide the
class of the candidate object by mapping the
feature vector into
decision space.
Eg: Nearest-neighbor classification.
Eg: Bayes optimal classification.
Eg: Vector quantization.
Eg:
Neural nets.
OR by synthesis: describe each candidate object
by a procedure for synthesizing that object.
Decide the class of the object by comparing the
synthesis procedure to stored class template
synthesis procedures.
Eg: Grammatical pattern classification.
Eg. Classification by production rules.
Eg. Sematic nets.
The first class of methods we will study employs analysis
based on feature vectors and probabilities. It was the
first pattern recognition method systematically devel-
oped, and probably today still the most common in
applications:
Statistical Pattern
Recognition
Our goal is to correctly classify objects. Assume there
are R classes of objects {ω1...ωR}
defined
in
the domain.
The statistical approach is to compute, for each possible
decision rule d() we might use,
Pr(
guess ω i
and true object is ωj | use d() ).
We can then decide, on the basis of these probabilities,
which d is best. For instance, we might select the d
that leads to the minimum probabilility of error. Or
we may define a loss function which varies
from error
to error, and select the
d which results in the minimum
average loss.
Let x=[x1 x2 .. xn]T be the feature vector, and
Ω ={ω1..ωR} be the set of class identifiers. Let
d: Rn-> Ω be a decision rule associating with each
possible value of the feature vector x a class
identifier. Let Dk(d)={x: d(x)=ωk} be the kth
decision region, ie. the region of feature space
that d classifies as ωk. The set of boundary points
between the decision regions are called the decision
boundaries or the discrimination hyper-surfaces.
If each of the discrimination hyper-surfaces is linear,
the decision rule is said to be linear.
Eg:
One way to determine these decision region
boundaries
is to define a set of discrimination functions gi(x)
{gi(x),
i=1..r}, gi:X->R1
and specify that the decision region Dk(x) is the set
of points x in feature space characterized by
Dk(x) = {x: gk(x)>=gi(x)
for
all
i=1..r}
So each decision region Dk(x) is determined to be the
region of feature space X where its discrimation function
gk(x) is the maximum
discrimination function.
Then the question for decision function design becomes,
how do we select the discrimination functions
{gi(x)} so
that the decision rule Dk(x) they
define is the one we want?
There are two classes of procedures for
computing discrim-
ination functions, and thus decision rules. One is based on
probabilities, and leads to statistical decision rules.
The other does not compute or estimate
probabilities and leads
to direct decision
rules. We will first look at a direct
decision rule, the minimum distance classifier.
Minimum distance
classifiers
First we must define a training set. Let a
single
correctly classified instance x,
ie. a duple {x,ω}
with x in X and ω in {1..R} be called a training
atom,
and
a
set
of such be called the training set
for this classifier.
Then the
minimum
distance
classifier is defined as
the classifier (decision rule dMD(x))
that
will
classify
an
unknown
instance x as belonging
to
class r if and only if
the nearest training atom to x is labeled
class r. The
sense of "nearest" can be chosen to be
Euclidean distance,
city
block distance or any other norm.
If the distance metric is selected to be
Euclidean,
then the classifier turns out to be geometrically
simple to visualize. This is due to the fact
that the
locus
of points equidistant from any two points in Rn
is
the hyperplane which is perpendicular to the
line segment
connecting these two points and passes
through the
midpoint of that line segment.
Using the Euclidean norm, if there is just
one
training atom
per class, the decision rule is always linear.

If there are two or more than one training atoms for at
least one class, in general the decision rule is
piecewise-linear.
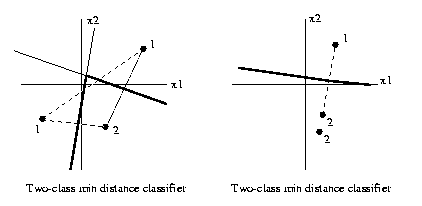
To determine the minimum Euclidean distance classifier
discrimination boundaries in R2,
1. Construct all the perpendicular bisectors of
pairs of training atoms with different class
labels.
2. For each such bisector,
say bisector A, mark a
point on it which is far distant from the
training set.
Determine if the two
atoms defining A are closer to it
than any other training atom. If so, move
in towards the
training set along this bisector until it
intersects
another one of the perpendicular bisectors
constructed
in step 1. Mark the segment
of A beginning at that point,
passing through the point where the construction began,
and going on to infinity as a
discrimination
segment.
3. Repeat 2. for the other
end of each bisector.
4. Define a bisector segment as a segment of
a bisector which lies between intersections with two
other bisectors, and contains no other such intersections.
For each bisector segment, determine if the two atoms
defining it are the closest atoms to it. If
so mark
that
bisector segment as a discrimination segment.
Mark all
bisector segments.
5. The union of all
discrimination segments found in
steps 2-4 above are the required
discrimination boundaries.
In terms of discrimination functions for
minimum
distance
classification we can use the set
gi(x) = 1/Gi(x)
where Gi(x) is the minimum over {xj,i} of training
data labelled class i of the distance between x and
xj. Any other monotone increasing function of this
minimum distance can be taken as gi(x) as well. To
keep the discriminant functions well-defined every-
where and avoid dividing by zero, the
definition
gi(x) = 1/(Gi(x)+1)
is often used.
Minimum error
classifiers
The problem of classifier design is to determine a
decision rule d(x) which tells us, for each x in the
feature space X, what classification we will assign
to an object which has that particular
feature
vector.
As we have seen, the decision rule can be
encoded in
the selection of a set of discrimination
functions
{gi(x),
i=1,...,R} which tell us how to
decide the class
of each x in X. For each x, d(x) will
evaluate to the
label i of the largest gi(x).
So lets assume we have an x we wish to classify. Let
P(ωr|x) denote the probability that the true class
is r, given that feature vector x. Then for minimum
error classification, we can assign a set of discrim-
ination functions
gi(x) = P(ωi|x)
So if we can compute P(ωi|x) for each x and each ωi,
we can use these probabilities as our
discrimination
functions, and have our minimum error
classifier.
How can we compute P(ωi|x)? The most common way is using
Bayes Law,
which
says
that
for
any
two
events
A
and
B,
P(A|B) = (P(B|A)P(A))/P(B)
Bayes Law follows from the definition of conditional
probability,
P(A|B)=P(A,B)/P(B)
thus
P(A,B)=P(A|B)P(B)=P(B|A)P(A)
The form we will use Bayes Law here is
P(ωi|x)=(P(x|ωi)P(ωi))/P(x)
P(ωi) is called the a priori probability of ωi.
This is the likelihood of class i before we see the
data x. P(x|ωi) is called the class-conditional like-
lihood of x given wi. P(x) is called the prevalence
of x.
What Bayes' Law tells us is how the a priori probability
of ωi is updated by the data x into the desired
a posteriori probability P(ωi|x). In other words, how the
data x has influenced our judgment of the
likelihood that
x comes from class ωi.
Eg: Prior probabilities: P(normal)=3/4,
P(sick)=1/4.
Based on a
blood test, we are given a feature vector
x with P(x|normal)=1/5, P(x|sick)=4/5. Then by Bayes Law,
P(normal|x) = (1/5)(3/4)/P(x) = 3/(20P(x))
P(sick|x) = (4/5)(1/4)/P(x) = 4/(20P(x))
So if we are doing minumum error classification, we
should classify this patient as sick, since
P(sick|x)>P(normal|x).
Eg continued:
P(sick|x) = P(x|sick)P(sick)/P(x)
P(normal|x) = P(x|normal)P(normal)/P(x)
so
P(sick|x)/P(normal|x)=
(4)(P(sick)/P(normal))
Thus if the prior probability of being normal is
more than 4x larger than that of being sick, we will
decide normal even though the evidence points strongly
to being sick ("likelihood ratio"
P(x|sick)/P(x|normal)=4).
Gaussian minimum error
classifiers
The most common form for the class-conditional probability
density functions (pdfs) in practice is the Gaussian, or
Normal, distribution given by
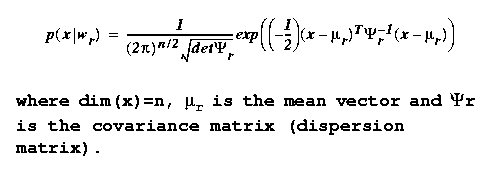
Now we showed previously that the posterior probabilities
P(ωr|x) form a min-error set of
discrimination functions
gr(x) = P(ωr|x) = P(x|ωr)P(ωr)/P(x)
Now any other set of functions {gr'(x), r=1..R}
which preserves the maximum (gk'(x)>=gi'(x) for
all i=1..R if and only if gk(x)>=gi(x) for all
i=1..R) will qualify as a set of discrimination
functions just as well as the gr(x)'s
above.
So lets multiply each gr(x), r=1..R by a common
factor P(x), the prevalence. This preserves
the maximum,
so we have a new set of discrimination
functions
gr'(x) = P(x|ωr)P(ωr)
Now let's define
gr''(x)
=
ln
gr'(x)
Since the natural log is monotone increasing,
this
also preserves the maximum, and thus defines
a new
set of discrimination
functions.
For the Gaussian case,
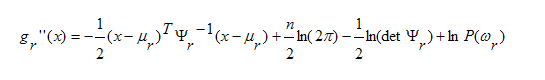
Now the decision hypersurfaces are x's where
the
maximum two gr(x)'s are equal. So
in the Gaussian
case they are parabolas. In the special case
that
the covariance matrices are all equal, the
quadratic
terms can be removed from the discriminants,
along
with the other common terms, leaving
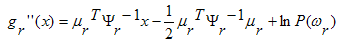
We conclude that in the Gaussian case with equal
covariance matrices, we have an important simplification:
the discrimination functions, and the decision hyper-
surfaces, are linear, ie. the decision rule
is
linear.
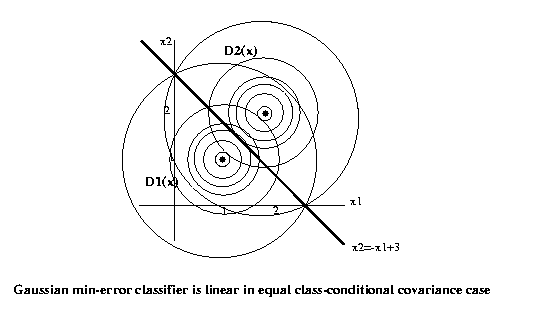
Eg: x = s + n, where for ω1, s
= [1 1]T and for
ω2, s = [2,2]T.
n
is
Gaussian with mean [0 0]T
and covariance
matrix
psi=[1 0; 0 1] (the identity
matrix). Assume the
two classes have equal priors.
Then
p(x|ω1) = 1/(2pi) exp(-1/2((x1-1)2+(x2-1)2))
p(x|ω2) = 1/(2pi) exp(-1/2((x1-2)2+(x2-2)2))
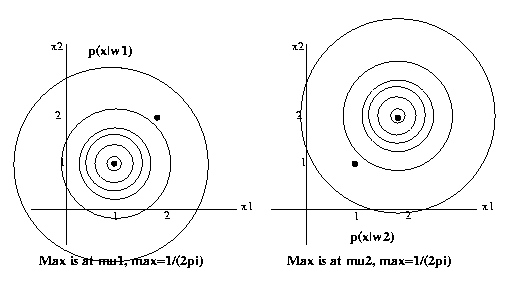
The discrimination hypersurface is where the two
discrimination functions
are equal,
[1 1]Tx-1/2*[1 1]T[1 1]+ln(.5) =
= [2 2]Tx-1/2*[2 2]T[2 2]+ln(.5)
or
x1+x2-1 = 2x1+2x2-4
which is the straight line
x2 = -x1+3
Minimum-average-loss
classifier
The minimum error classifier implicitly treats all
errors as equally undesirable, and all correct class-
ifications equally desirable. But in practice this is
often not the case.
Eg: In a medical screening test, false negatives
are usually more costly than false positives,
and true positives are more valuable than true
negatives.
Eg: In a speech driven operating system,
classification errors leading to logouts or
system crashes are worse than those opening a
dropdown menu.
Define a loss function λ:{1..R}X{1..R}->R1 such
that λ(ωr|ωs) is the loss sustained if a sample is
classified as ωr when its true class is ωs. Suppose we
are required to classify the sample x. The minimum-
average-loss classifier, also referred to as the
Bayes-optimal classifier, is the one which classifies
x as d(x)=ωr where ωr minimizes the expected loss
for this value of x,
d(x) = ωr = arg
min ωi { E[λ(ωi|ωs,x)] }
In this expression the expectation is taken over ωs
with ωi and x fixed.
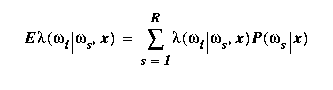
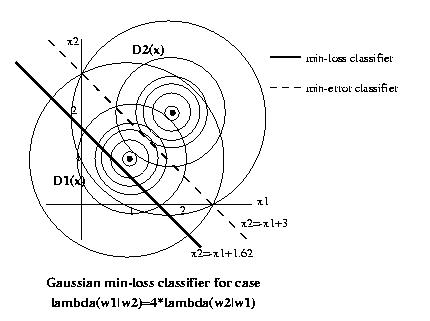
Eg: Previous example with P(ω1)=P(ω2)=1/2. Lets use a
loss function λ(ω1|ω2)=4, λ(ω2|ω1)=1,
λ(ω1|ω1)=λ(ω2|ω2)=0.
Then
E λ(ω1|ωs,x)=4*P(ω2|x)
E λ(ω2|ωs,x)=1*P(ω1|x)
So the discrimination hypersurface will be the set
of x such that 4*P(ω2|x)=P(ω1|x). But, cancelling
common factors of P(x) and 1/2, by Bayes' Law this
is
P(x|ω1)
=4*P(x|ω2)
Equating two exponentials and taking logs, this
turns out to be a linear
decision rule.
ln P(x|ω1) = ln P(x|ω2) + ln 4
where
P(x|ω1) = 1/(2pi) exp(-1/2((x1-1)2+(x2-1)2))
P(x|ω2)
=
1/(2pi)
exp(-1/2((x1-2)2+(x2-2)2))
(x1-1)2+(x2-1)2 = (x1-2)2+(x2-2)2-2.77
-2x1+1-2x2+1 = -4x1+4-4x2+4-2.77
x2 = -x1+1.62
If we are not given the
required
probabilities
In order to find the minimum-error or Bayes' optimal
classifier, we need to know all the class-conditonal
pdf's {p(x|ωi), i=1..R} and all the a priori probab-
ilities {P(ωi), i=1..R}.
Sometimes we assume this information is assumed to
be known and given to us during the off-line design
stage before on-line operations. In this case we have
a complete stochastic model for the classification
problem. Complete stochastic models require two
things:
1. Lots of data, or complete theoretical domain
knowledge;
2. The assumption that the probabilities are
invariant
during on-line operations.
If these conditions are not met, we must learn while
on-line
(while classifying) rather than in advance
while off-line
during training. Learning is the
adaptation of an algorithm or behavior in
light of
actual
experience.
Eg: In a character classifier problem, we begin with
a priori probabilities P('a'), P('b'), etc. taken
from a general English language database. But in
the book we are translating, we find that the
letters 'x', 'y', 'z' show up much more frequently;
the letter 'e' much less frequently. We recompute
priors according to the
"hits-to-trials" ratio
P(wi) = (instances of wi
so
far)/(all letters so far)
Proceeding in this way, we
are learning the
correct
priors not in general for
the English language, but
for this book.
Eg: We know that x = s + n, and we know that n is
Gaussian, but we don't know what its mean vector
or covariance matrix are. We use a method for
estimating these quantities from the training
training data seen so far.
Suppose we are given a set of training data {x1..xn}
whose true class is ωk.
Estimating the
mean μk
of a
Gaussian:
μk~
=
1/n
(x1+..+xn)
where μk~ is the estimate of μk after n training
data. Our estimate of the mean is just the sample mean.
This is not the only feasible estimate of the mean,
but it has many nice properties and is usually chosen.
It is minimum-variance unbiased, maximum likelihood,
asymptotically efficient and asymptotically
normal.
Estimating the covariance matrix ψk of a Gaussian:
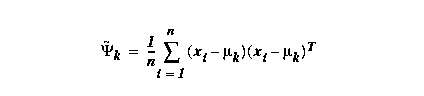
a Gaussian: use μk~ above for the mean estimate,
then replace μk in the covariance estimate by this
μk~ ; also
replace 1/n by
1/(n-1).
Syntactic approach
to object recognition
So far we have considered the statistical approach
and the min-distance approach, in which objects are
characterized by their features.
In the syntactic approach, we construct a description
of an object in a selected formal language. Each
object class ω1..ωR is characterized by a grammar,
that is, a set of alphabets and relations which
govern what strings of symbols from the formal
language are "legal" for objects of that class.
When we have found an object class for which the
given object description is grammatical, we declare
a match to that object class.
Formally, a grammar is a 4-tuple G=[Vn,Vt,P,S]
where
Vn is the set of non-terminal symbols;
Vt is the set of terminal symbols (primitives);
P is the set of production rules;
S is the start symbol.
We always start with S, then choose a production
rule to replace a non-terminal (intially S) by a
terminal symbol or combination of terminals and
non-terminals. We keep going until the string
contains only terminals. That is the "word" we have
created using the grammar.
Eg: Consider the following code grammar which
produces
"complementary mirror
codes" (CMCs):
Vt = {0,1,E}
Vn = {S,X}
P = {S->XE,
X->0X1|1X0|01|10}
Then for instance if we receive the string
00101011E
we find it is grammatical using the CMC grammar,
since
S->XE->0X1E->00X11E->001X011E->00101011E
Types of grammars
The more general the grammar the more expressive
it is; the more constrained the grammar the easier
it is to parse.
Let x be an element of Vt; a and b be elements of
Vn, A, B and C be grammatical strings of primitives
from Vt U Vn where the
symbol U refers to set union,
and e be
the
empty set. Then we can distinguish four
types of grammars, from the least constrained
to the
most general:
Type 3: Regular grammars (finite grammars):
Left regular: a->xb|x
Right
regular:
a->bx|x
In other words, a regular grammar works by writing
a terminal symbol and moving to a new nonterminal
state. Type 3 grammars are represented by
finite-state automata, which makes them easy to
parse.
Type 2: Context-free grammars:
a->A
In other words, a non-terminal can be replaced by
any grammatical string independent of the symbols
surrounding it (independent of context).
Type 1: Context-sensitive grammars:
AbC->ABC
In other words, the non-terminal b can be replaced
by the string B but only if it is surrounded by the
specific strings A and C, ie. only in this
context.
Type 0: General grammars:
unconstrained.
Regular grammars and
Finite-State Automata (FSA)
Each regular grammar corresponds to an unique
FSA.
The non-terminals are the nodes and the automata
writes a terminal along each arc. There is one
additional node, the end node (an absorbing
state), which is the only FSA node explicitly
referenced in the regular grammar.
Eg: 4-bit code with odd parity.
P={S->0a|1b, a->0c|1d, b->1c|0d, c->0e|1f,
d->1e|0f, e->1, f->0}
Here is the corresponding FSA:
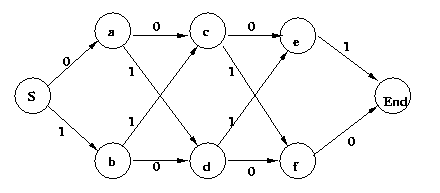
Often the easiest way to construct a regular
grammar
from a "word problem" description, is to
first construct
the FSA. The key to constructing the FSA is
to note
that each node in a FSA is a different state
in the
construction of the string, i.e. what you
need to know
in order to finish the string grammatically
from there.
The formal grammar, i.e. the 4-tuple, then
follows
directly from the FSA.
Eg: Above, node a: odd parity so far, 3 more
symbols to go
node
c:
even
parity
so
far, 2 more to go
etc.
Parsing is the process of analyzing a given string to
determine if it is grammatical, and if so, what sequence
of production rules produced it. The more general the
grammar, the harder it is to parse.
Regular grammars can be parsed by constructing a parse
tree. If
the parse tree does not have a branch that
terminates immediately after the last
terminal, the
string is not grammatical.
Eg: Determine if the string 001101001 is grammatical in
the regular grammar represented by the FSA
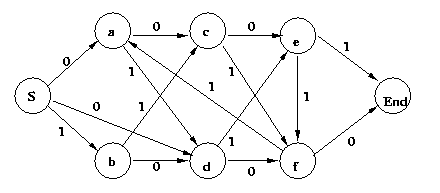
Start the construction by writing the terminals
vertically
down a sheet of paper. Then beginning with node S at the
top, draw an arc to each node in the FSA you may reach by
outputting the given terminal. Proceed until you reach the
end of the string, or no further arcs are
possible.
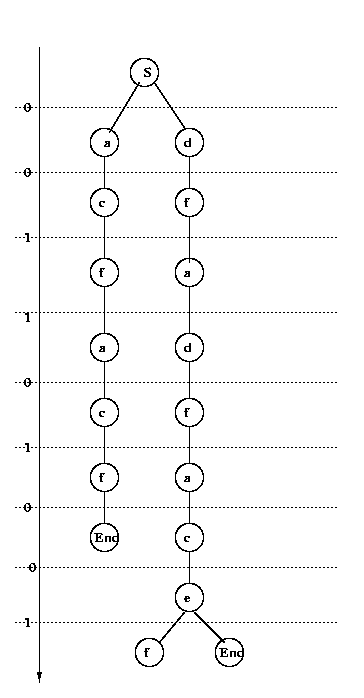
Conclude that the string is grammatical and the
unique sequence of productions is
S->0d->00f->001a->0011d->00110f->001101a->
->0011010c->00110100e->001101001
Parsing is more difficult with Type 0-2 grammars
since they cannot be represented by FSA's nor parsed
using the simple parse tree described above.
Grammatical inference is the process of inferring a
grammar from a set of examples. For any finite set
of consistent examples, there exists at least
one FSA,
and hence a regular grammar, that produces
this set of
examples as its language. This is why regular
(Type 3)
grammars are also called finite grammars.
But while every finite language has a finite grammar,
there may be a simpler Type 0-2 grammar with
many fewer
non-terminals and production rules. Training of
syntactic pattern recognition systems using grammatical
inference is an active area of current
research.
Neural Nets
Neural nets have been on the scene a very
long
time,
perhaps a half billion years. The ability of
biological
neural nets to produce intelligent behavior in animals
and man has inspired the design of artificial neural nets.
Biological neural nets:
Information processing in the human brain
takes place in
a vast interconnection of specialized cells
called neurons.
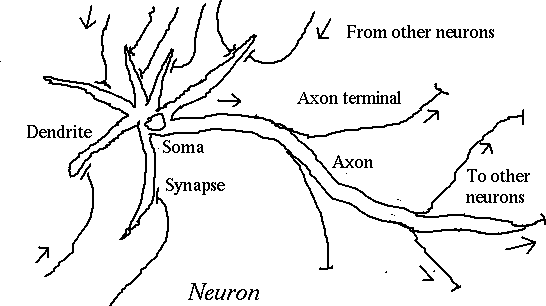
When the cell body (soma) reaches threshold
potential,
an action potential is fired down
the axon.
An action
potential is a 1-2 ms
reversal of polarity of
the cell membrane from negative to positive.
Here is an image of a group of neurons taken from the primary
hippocampal region of a rat. The specimen was stained with different
dies to bring out the cell body, dendrites and axon.
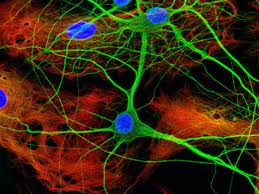
Source:
nikonsmallworld.com
When the action potential reaches a synapse,
or connection
with another neuron, it causes a
neurotransmitter
to flow
into the synaptic cleft.
The neurotransmitter causes the post-synaptic
membrane to
become more negative (inhibitory synapse) or
more positive
(excitatory synapse).
The net effect of all the post-synaptic
membrane stimuli
is to change the soma potential closer to or
further from
threshold.
In a human brain,
Conclude:
Artificial neural nets
An artificial neural network is a highly
parallel
interconnection of simple
computing elements called
artificial
neurons.
Eg.
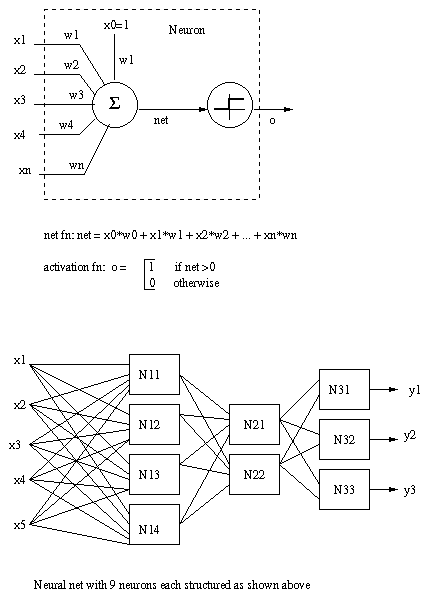
How do artificial
neural
nets work?
Neural nets are trained to learn a desired
target function
t: X -> Y
where X is the space of input vectors and Y
the output
vectors. The output y=t(x) of the neural net is the "right" output when
the input to the neural net is x.
Typically the network
topology (number of inputs, outputs,
neurons, and their interconnections) and
the selection of
net and activation functions for each neuron, is
fixed.
Learning proceeds by modifying the weights Ω =
( ω0,...,
ωnw).
Consider one particular assignment of numerical values for all nw
weights as a point in an nw-dimensional space. One point in this space
is the true target function, its location is what we are trying to
learn. The unbiased
hypothesis
space
is Rnw. Each point in this space is a hypothesis, or guess,
as to what the target function is.
Eg.
For preceeding diagram, there are (remember
the
bias
inputs):
6x4 + 5x2 + 3x3 = 43 weights
The
hypothesis
space
H
is
the
43
dimensional
set
of
real
numbers
ω
=
R43. Learning is moving
from
point
to
point
in
R43 until a solution
is
found.
Learning as search
over weight space
How do we search the unbiased hypothesis
space H = Ω = Rnw?
How
do we
recognize a hypothesis that is
better than our
current one?
Start by specifying a training
dataset D:
Training dataset D:
A
set
{(xi,ti)}of input
vectors xi and
their
corresponding target vectors ti.
Let ω in Rnw represent the current
weight vector. We
can
assess how well we are
doing by passing xi through the
system, noting the output oi, and
determining the
error (ti-oi). Then the total sum-squared error is:
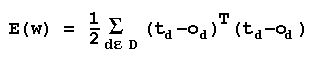
The error manifold
E(ω) can be
visualized as a landscape
being crawled over by an ant searching for the
lowest
valley. That lowest valley is at the solution
ω*, the
hypothesis in H which minimizes the error over D.
Gradient descent
How should we crawl
over
E(ω)? Gradient descent is the
approach based on finding
the direction of steepest
descent, which is the negative gradient
direction


Eg: Gradient descent over a 2-dimension weight space Ω
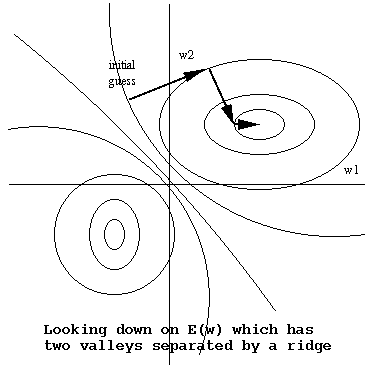
Note that gradient descent will find a nearby
local
minimum, not necessarily the desired global
minimum.
The Gradient Descent Rule
Let's apply gradient
descent to ANN's with no hidden layers.
With E(ω) as our
sum-squared error defined previously,
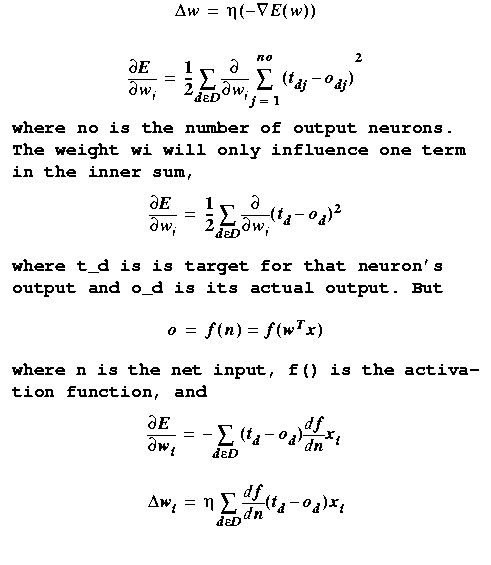
If we only consider the most recent error, we
have
just the last term in the Gradient Descent Rule,
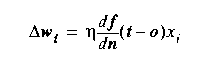
This is the Delta
Rule. It is an incremental (rather than
batch) approximate gradient descent learning
rule. It computes
the next weight vector much faster than Gradient Descent by
ignoring all but the current error. The payback is that many
more weight changes are required to convergence.
The Gradient Descent Rule, or its variant the
Delta Rule,
can be extended to neural nets with hidden
layers. A small
change in the weight ωi will effect
its
neuron's outputs
and all neuron outputs downstream from it. So
using the
chain rule, we can compute the partial of
the error
with respect to ωi even for weights
of hidden
units.
This extension is called the backpropogation training
rule. See text page 311 for details.
Eg.

A small change in ω5 will cause the outputs of its neuron and all the output neurons to change, thus changing the errors at each output neuron.
CSE 573 Fa2010 Peter Scott 07-49
Eg: Classifier for a circular subsetAs an example, let's use a two-input (2 input neurons), one-hidden-layer (8 hidden neurons), single-output (1 output neuron) neural net to try to learn to correctly classify points that fall inside a circular window. The target function we are trying to learn is that the neural net output should be 1.00 for input points that fall inside the circle, 0.00 for points outside the circle.
13 training atoms were used, with assigned target value of output 1.00 for the 5 points inside the circle, and 0.00 for the 8 points outside the circle.
CSE573 Fa2010 Peter Scott 07-50
The results shown below were computed using the Matlab Neural Net toolbox. It is available on all the UB machines. User guide with tutorials here.
After one epoch of training, weight training was stopped and the neural net tested. The image below shows the result after one epoch. The output for every possible input in the range [0,1]x[0,1] is shown. Output values are coded as grey levels with pure black 0.00 and pure white 1.00. Ideally, this graph should be pure white inside the circle and pure black outside it.
The mse=0.33 (stderr=0.57) after this one epoch of training.
CSE573 Fa2010 Peter Scott 07-50a
After two epochs the mse is down to 0.13. It is coming closer to the desired white circle.
With additional epochs the mse decreased to about 0.09, but did not decrease further. That is because we did not have sufficient training data for the neural net to "figure out" it was supposed to be white inside a circle of radius 1/4, black outside it. With many training atoms, and many epochs, we could learn the circle with as small an error as desired.
CSE573 Fa2010 Peter Scott 07-51
Other classes of neural nets and training rules
Thus far we have discussed only feedforward
(acyclic) ANNs taught using supervised training
(input, target output training atoms).Unsupervised neural nets learn how to cluster data in natural groupings. Instances which are (in some
sense)similar to each other are assigned to the
same cluster.Eg:
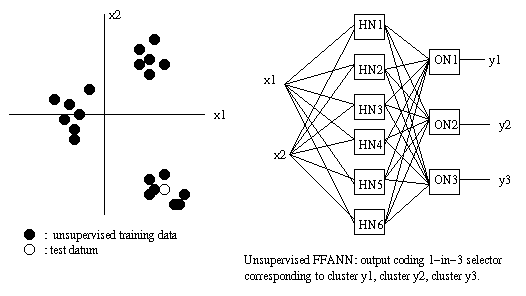
If the cluster at 4 o'clock corresponds to
y2, then when the test datum comes in, the
three outputs will be 0, 1, 0 respectively.An example of an unsupervised neural net is
the Kohonen selforganzing net. Another is the
Carpenter-Grossberg or ART net.
CSE573 Fa2010 Peter Scott 07-52
Recurrent neural nets have closed cycles in their
directed graph representations. The feedback paths
permit more complex behavior than feedforward nets.The Hopfield net is a recurrent neural net which
operates as an associative memory. A weight matrix
Ω is formed from the set of patterns to be
remembered and y(k+1)=Ωy(k) iterated until the net
converges to a stable solution.Eg:
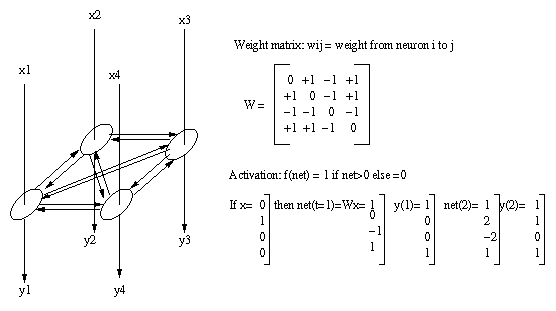
For all t>2, net(t) and y(t) do not change.
Output is y(2).
CSE573 Fa2010 Peter Scott 07-53
Graph matching approach
to object recognition
If the object is described by its features, then we
can use statistical methods or neural net methods for
object recognition. If it is represented as a string
of primitive symbols, syntactic methods may
be
used.
Another common method of describing objects is as
graphs. In the simplest case the nodes represent
the object parts and the arcs represent adjacency.
This results in an undirected, unevaluated graph.
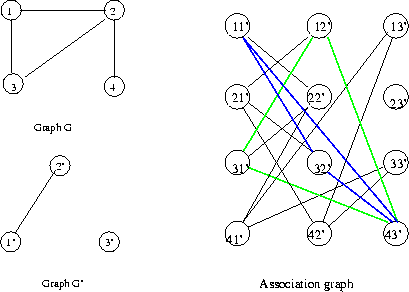
Eg:

Now if scenes (or segments of scenes) and class exemplars
are represented as graphs, object recognition amounts to
matching graphs or portions of graphs.
Eg:
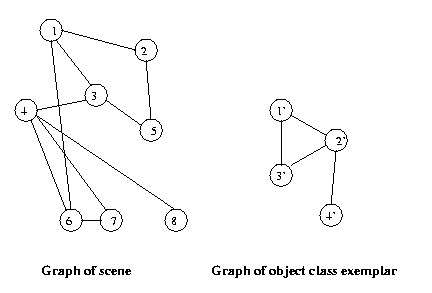
Note that there are instances of this object class
hidden in the scene.
Formally, a graph G(V,E) is a set of vertices V and edges
E. If the vertices are simply enumerated 1,2..N and the
the edges are designated only by the two vertices they
link without regard to order, G is called a non-evaluated,
non-directed graph. If the edges have arrows (order of
vertices in their descriptions counts) the graph is
directed, if the vertices ("nodes") or edges have
any additional attributes the graph is said to be
an evaluated ("attributed") graph.
The goal of graph matching is to find an invertible
node association function vj'=f(vi) between two graphs
G(V,E) and G'(V',E') such that for all k and
l,
1. There is an edge in E connecting vk and vl
if and only if there is an edge in E' connecting
f(vk)
and
f(vl);
2. For directed graphs, there is an edge directed
from vk to vl in E if and only if there is also
an edge
directed from f(vk) to f(vl) in E';
3. For evaluated graphs, nodes vk in E and f(vk)
in E' have identical values, also the edges
connecting vk and vl in E have the same values
as those
connecting f(vk) and f(vl) in E'.
The function f is called the node association function.
In other words, for graphs to match they have to have
the same connectivity, corresponding nodes need to have
the same properties, and corresponding edges need to
have the same properties.
If we match an entire graph against an entire graph, this
is called a graph isomorphism. If we match a portion of
one graph against an entire other graph, this is a
sub-graph isomorphism. If we match a portion of one graph
against a portion of another, this is a double sub-graph
isomorphism.
Eg: We are looking for squares in a scene. If we
segment out a particular object from the scene
and match it to the square graph, thats a graph
isomorphism problem. If we match the graph of
the square to the entire scene, we are
seeking a sub-graph isomorphism. If we have two
scenes both containing squares and match them
looking for squares, that's a double sub-graph
isomorphism problem.
Eg: continuing a previous example, we had the
non-directed, non-evaluated pair of graphs

In G, the left graph, V={1..8} and E={(1,2),(1,3),
(1,6),(2,5),(3,5),(4,6),(4,7),(4,8),(6,7)}.
In G', the other one, V'={1'..4'}, E'={(1',2'),
(1',3'),(2',3'),(2',4')}.
Consider the node assocation function f defined by
the table
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In order to declare a match, we need to make sure
that an edge exists for a pair of v's if and only
if it exists for the same
pair of f(v)'s.
Check: (4,6) in E, (f(4),f(6))=(2',1')=(1',2') in E'.
(3,6) not in E, (4',1') not in E'.
etc.
So f constitutes a valid node association function,
and we have found a sub-graph isomorphism between
these two graphs.
Note: there are 3 distinct subgraph isomorphisms
involving G and G, not
just the
one we discovered
above.
Note that in this example, if the graphs were
directed (arrows pointing towards the second
node in their descriptions), then the given f
would not constitute a legal node association
function, since (4,6) in E is not matched by
(f(4),f(6))=(2',1')~=(1',2') in E'.
Or if node 3 had the value "blue" and node
4' had the value "red," then f would not
work for these
evaluated graphs.
A useful technique for finding matches between two graphs
is based on the assignment graph.
This is a
matrix-shaped
graph whose rows are the nodes in G and
columns the nodes
in G'. Each matrix location is a node in the
assignment
graph.
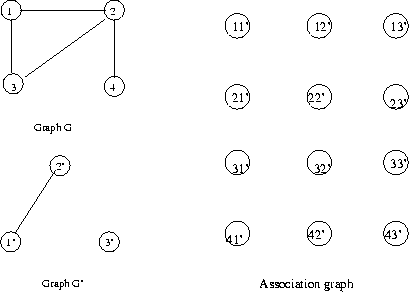
Eg: Nodes in the assignment graph for the previous eg.

Each pair of nodes in the assignment graph is inspected
to see if an edge should be drawn between them. The rule
is that they are connected if and only if the pair of node
associations (nodes of the assignment graph) are
consistent.
Consistency
requires
that
1. The connectivity between the two G-nodes matches
the
connectivity between the two G'-nodes,
2. The direction of
connectivity (if any) matches,
3. The values (if any) of the corresponding nodes
match,
4. The values (if any) of the corresponding edges
match.
Only 1. is relevant for
undirected unattribed
graphs.
Eg: Continued: For instance, the node association
1 1' is consistent with 6 3' because there is an
edge between 1 and 6, also between 1' and 3'. So
in the assignment graph we draw an edge connecting
nodes 1 1' and 6 3'. Also, 1 3' is not consistent
with 3 4' because ther is an edge between 1 and 3
but not between 3' and 4'.
After all legal edges are added to the assignment graph,
the matches can be readily found. A clique is a fully
connected set of nodes in a graph. Each clique in the
assignment graph specifies a legal node association
function and thus (in general) a double sub-graph
isomorphism. The maximal clique in the assignment
graph represents the largest matching set of nodes
in the two graphs. If G has n nodes and G'
has m, then
a maximal clique with k matching nodes in
each graph
defines a:
1. Graph isomorphism if
k=n=m;
2. Subgraph isomorphism if
k=n or k=m but not both;
3. Otherwise a double
subgraph isomorphism.
Example:
Start with node 11'. Consider all possible
links
to nodes in second row. Since nodes 1 and 2
are
connected, add a link to each node in row 2
whose
G' node is connected to 1'. Repeat for row 3:
Since
nodes 1 and 3 are connected, add a link to
each node
in row 3 whose G' node is connected to 1'.
Repeat
for row 4: since nodes 1 and 4 are not
connected,
add a link to each node in row 4 whose G'
node is
not connected to 1'. This completes node 11'.
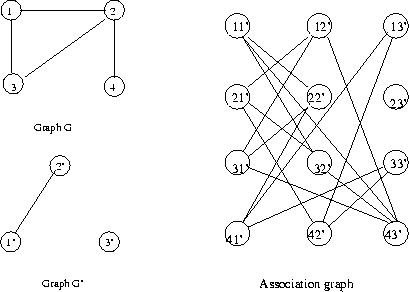
Repeat for each node in the association
graph. Note
that links are not possible between nodes in
the
same row or column. If you work from the top
row
down, note that while computing the links for
a given
node in a given row you need only check for
links
to nodes in rows below.
The final association graph for this example is

There are two maximal cliques (3 nodes)
corresponding to two
maximal subgraph isomorphisms.