CSE668 Lecture Slides Spring 2011

2. 3-D Imaging Models

Required reading: Sonka Ch 9.

Recommended: Trucco Ch 9.

Part I of this course, on early vision, is concerned

with the most basic vision tasks, such as determining

the depth of a given image feature from the camera, or

estimating egomotion (camera self-motion). Part II,

on late vision, covers the more complex vision

tasks, those which build on early vision

capabilities (eg. tracking, object recogntion). Part

I will take us up to the midterm exam.

We first consider the traditional passive vision

approach, and then the more recent active vision

approach to early vision.

CSE668 Sp2011 Peter Scott 02-00

---

Passive early vision

3-D Imaging models

In passive vision analysis, we work closely with our

imaging system's imaging model, that is, its quantitative

mapping from 3-D scenes to 2-D images. Then the main job

can be undertaken: to invert the imaging model, that

is, recover the 3-D scene. Recall that Passive Vision

is synonymous with Vision as Recovery.

CSE668 Sp2011 Peter Scott 02-01

---

Camera model

In order to have a quantitative description of how

a given camera views the real world, we need a camera

model. This is a mapping C: R³->R² which specifies

how the 3D scene will appear on the 2D image plane of

the camera. A camera model supports two types of

parameters:

Intrinsic parameters: properties of the camera

    itself, which do not change as the position and

    orientation of the camera in space are changed.

Extrinisic parameters: those which change with

    position and orientation of the camera.

CSE668 Sp2011 Peter Scott 02-02

---

Eg: focal length and lens magnification factor are

    intrinsic parameters, focal point location and

    vector orientation of the optical axis are

    extrinsic parameters.

Both sets of parameters must be completely specified

before the camera model C: R³->R² is known and we can

predict the 2D image on the image plane that derives

from any given 3D scene.

CSE668 Sp2011 Peter Scott 02-03

---

Perspective projection

The geometry of perspective projection is used to

develop the camera model.

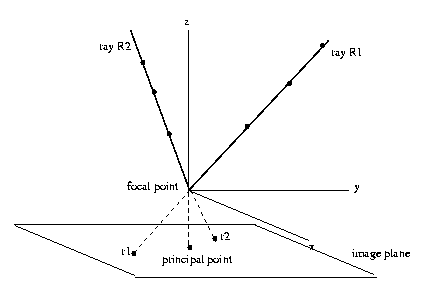
Define a ray as a half-line beginning at the origin.

CSE668 Sp2011 Peter Scott 02-04

---

All points on a given ray R will map into the

single point r in the image plane. The set of

all such mappings is the perspective projection.

CSE668 Sp2011 Peter Scott 02-05

---

Formally, let x and x' be nonzero vectors in Rⁿ⁺¹

(we will use n=2) and define x == x' (x is

equivalent to x') if and only if x'=αx for some

scalar α not equal to zero. Then the quotient

space of this equivalence relation (set of

equivalence classes) is Pⁿ, the projective space

associated with the Euclidean space Rⁿ⁺¹. Note

that for the projective space is lower-dimensional

than the Euclidean space (dim = 2 vs 3).

CSE668 Sp2011 Peter Scott 02-06

---

Informally, points in P² can be thought of,

and represented, as follows. Take a point in R³,

say [x y z]^T, write as z [ x/z y/z 1]^T (z~=0).

Then [x y z]^T in R³ maps into the point

r = [x/z y/z] in P².

Eg: [30  15   5]^T -> [6 3]^T

    [ 3 3/2 1/2]^T -> [6 3]^T

    So these two points in R³ project to the

    same point [6 3] in the projective space P².

CSE668 Sp2011 Peter Scott 02-07

---

The pinhole (single perspective) camera model

^{This is the simplest possible lensless camera model.}

^{Conceptually, all light passes through a vanishingly}

^{small pinhole at the origin and illuminates an image}

^{plane beneath it. The geometry here will be quite}

^{simple. Most of the work in understanding the model}

^{will be in keeping several distinct coordinate}

^{systems straight.}

CSE668 Sp2011 Peter Scott 02-08

---

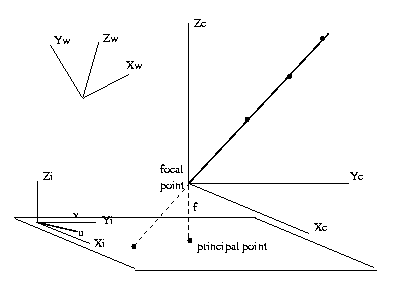
(X_w,Y_w,Z_w): World coordinates. Origin at some           
            arbitrary scene point in R³.

(X_c,Y_c,Z_c): Camera coordinates. Origin at the
            focal point in R³.

(X_i,Y_i,Z_i): Image coordinates. Origin in the image plane,
            axes aligned with camera coordinate axes.

(u,v,w): Image affine coordinates. Same origin as

         image coordinates but u and X_i axes may
         not coincide (others do coincide), and

         there may be a scaling.

CSE668 Sp2011 Peter Scott 02-09

---

Recall that the camera model is a mapping C:R³->R²

which takes us from world 3D coordinates to (u,v)

image affine coordinates. We will develop the

camera model in three steps:

Step 1. (x_w,y_w,z_w)->(x_c,y_c,z_c) world to camera coords.

These two 3D Euclidean coordinate systems differ by

a translation of the origin, and a rotation in R³, ie

by an affine transformation.

CSE668 Sp2011 02-10

---

This coordinate transformation is given by

                  X_c = R(X_w-t)

where       X_w = [x_w y_w z_w]^T is a 3D point expressed

                in world coordinates;

            X_c = [x_c y_c z_c]^T is the same point in

                camera coordinates;

            R is the 3x3 rotation matrix (pitch,

                roll, yaw);

            t is the translation vector (origin of

                camera coordinates expressed in world

                coordinates).

Note that R and t are extrinsic parameters of the

camera model, since they change with change of

camera location (t) and orientation (R).

CSE668 Sp2011 02-11

---

Step 2: Project the point in camera coordinates

onto the image plane, keeping camera coordinates.

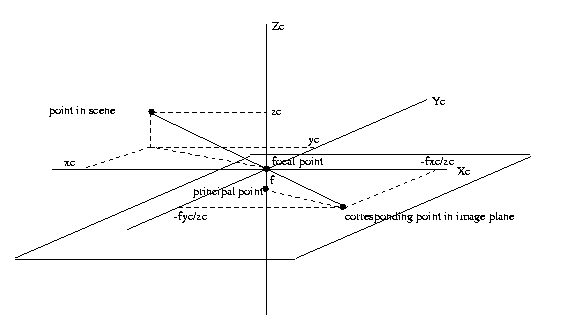
The coordinates of the corresponding point in the image

plane, retaining camera coordinates, are

            U_c = [-fx_c/z_c  -fy_c/z_c -f]^T

CSE668 Sp2011 02-12

---

Step 3: U_c->(u,v), the image affine coordinates in the

        image plane. The image affine coordinates are

        related to the Uc camera coordinates projected onto

        the image plane [-fx_c/z_c  -fy_c/z_c]^T by a further

        translation of the origin, scaling, and possible

        shear of the x-axis (rotation of the x axis with

        respect to the y axis).

[u v]^T = S [-fx_c/z_c  -fy_c/z_c]^T - [u₀ v₀]^T

        where

            [u v]^T =  final image affine coords in the

                      image plane

            S = 2x2 matrix of form [a b; 0 c]

            [u₀ v₀]^T = principal point expressed in

                      image affine coordinates.

CSE668 Sp2011 02-13

---

The S-matrix represents the scaling (a,c) and shear of

the x-axis (b). The vector [u₀ v₀]T is the translation

of the origin between the Euclidean image coordinates

and the affine image coordinates in R².

This set of results can be expressed in a compact way using

homogeneous coordinates. These are coordinate vectors whose

last entry is the constant value 1. Let

[u v 1] = [ a b -u₀; 0 c -v₀; 0 0 1][-fx_c/z_c -fy_c/z_c 1]^T

      = [-f_a -f_b -u₀; 0 -fc -v₀; 0 0 1] [x_c/z_c y_c/z_c 1]^T

which agrees with the translation, scaling and shear coord

transformation equation of the preceeding slide.

Designating the 3x3 matrix as K, the camera calibration

matrix and multiplying by z_c we get

            z_c [u v 1]^T = K [x_c y_c z_c]^T

CSE668 Sp2011 02-14

---

Note that the the camera calibration matrix K contains the

intrinsic parameters of the camera model, those that do

not change as we relocate and reorient the camera.

So putting the pieces from Step 1 and Step 3 together,

           z_c [u v 1]^T = K [x_c y_c z_c]^T

and recalling the relationship between camera and world coords:

  Pinhole camera model:  z_c [u v 1]^T = K R ([x_w y_w z_w]^T - t)      

The completes the camera model PCM, which maps points from

world coordinates [x_w y_w z_w]^T in R³ to image coordinates [u v]^T

in R².

To use the PCM, we must know both the extrinsic parameters

(R, t) and the intrinsic parameters (K). Then for any input

world point [x_w y_w z_w]^T we plug in to the right hand side, and

after evaluating the RHS, convert the result to homogeneous

coordinates by factoring out the value of the last (third)

coord to get the desired form z_c[u v 1]^T.

CSE668 Sp2011 02-15

---

Eg: Extrinsic parameters: Assume the camera

    coordinates represent a +30 degree cw

    rotation in the xy plane relative to the

    world coordinates, and that the origin of

    the world coordinate system is located at

    [2 2 0]^T in camera coords.

    Intrinsic: f=4, the image coords (u,v)

    are both scaled by 2 relative to the

    camera coords, there is no shear, and

    the image affine coord origin is at the

    principal point of the camera.

    Find the (u,v) location of the world point

    [9 3 3]^T and the ray that maps to that

    point.

CSE668 Sp2011 02-16

---

    Extrinsic:

    R = [cos30 sin30 0;-sin30 cos30 0; 0 0 1]

      = [.866 .5 0; -.5 .866 0; 0 0 1];

Note: the lighter font weight indicates Matlab notation

    t :            X_c = R(X_w-t)

         since X_w=[0 0 0]^T is the world origin,

         X_c = R(-t) yielding t = -R^-1X_c

       = [.866 -.5 0; .5 .866 0; 0 0 1]*[2;2;0]

= [.732;2.732;0]

CSE668 Sp2011 02-17

---

Intrinsic:

    K = [-fa -fb -u₀; 0 -fc -v₀; 0 0 1]

where f=4, a=c=2 and b=0, u₀=v₀=0, so

    K = [-8 0 0; 0 -8 0; 0 0 1]

    Plugging these values into the camera model

z_c [u v 1]^T = K R ([x_w y_w z_w]^T - t)

the world point [9 3 3]^T maps to the homogeneous

    affine image coordinates

K R ([9 3 3]^T - t) = K R [8.268 .268 3]^T

        = [-58.4 +31.2 +3]^T

        = 3[-19.5 +10.4 1]

    So (u,v) = (-19.5,+10.4) in affine image coords

    on the image plance.

CSE668 Sp2011 02-18

---

    Also, the camera coordinates of the world point

    [9 3 3]^T are

        X_c = R (X_w - t)

    and plugging the values we have for R and t,

X_c = [.866 .5 0; -.5 .866 0; 0 0 1]*[8.27;.268;3]

= [7.29;-3.90;3]

In homogeneous coordinates this is

    X_c = 3[2.43 -1.3 1]

 So in camera coordinates, the ray consitutes the set

 of points α[2.43 -1.3 1] for positive scalars α.

CSE668 Sp2011 02-19

---

The pinhole camera model PCM: [x_w y_w z_w]^T -> [u v]^T

       z_c [u v 1]^T = K R ([x_w y_w z_w]^T - t)

can be put into an even more useful linear form

by expressing the world coordinates homogeneously.

    z_c [u v 1]^T= [K*R  -K*R*t][X_w;1]

Or using homogeneous notation u~ = z_c[u v 1]^T ,

X_w~ = [x_w y_w z_w 1]^T we have the camera model in

homogeneous coordinates

                u~ = M X_w~

where M is the 3x4 matrix M = [K*R  -K*R*t] called

the projective matrix. Note: tildes (~) after a variable

here correspond to tildes above a variable in the

Sonka text.

CSE668 Sp2011 02-20

---

Determining the projective matrix M

The easiest way to determine M is by determining

the image of a known scene, one in which the

world coordinates of a number of points are

known and their corresponding image points are

also known.

As shown in Sonka 2/e eq. (9.14) p. 455, each (x,y,z)->(u,v)

world-point-to-image-point correspondence defines

two constraints between the 12 elements of the

projective matrix:

    u(m₃₁x+m₃₂y+m₃₃z+m₃₄)=m₁₁x+m₁₂y+m₁₃z+m₁₄

    v(m₃₁x+m₃₂y+m₃₃z+m₃₄)=m₂₁x+m₂₂y+m₂₃z+m₂₄

CSE668 Sp2011 02-21

---

So with as few as 6 such measurements we can

determine the m matrix as the solution of 12

linear equations in 12 unknowns. With more, we

can find the least squares solution for M, a much

more robust procedure.

Procedures also exist for finding M in more

complex cases, such as a scene in which the

locations of the corresponding points are

not known a priori, and where there is image

motion.

CSE668 Sp2011 02-22

---

Steropsis

Stereopsis is the determination of 3D geometry

from a pair of 2D images of the same scene.

The basis of stereopsis is that if we know the

projective matrices for each of the two cameras,

and if we have the two points u_l~ and u_r~ on

the left and right camera image planes, then

we can determine the ray for each camera, and

the intersection of these two rays yields the

location of the corresponding point in the scene.

CSE668 Sp2011 02-23

---

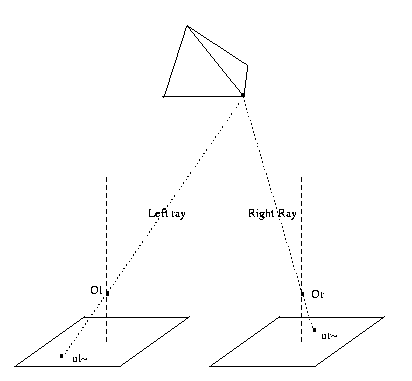
So stereopsis, ie. the recovery of the 3-D location

of scene points from a pair of simultaneously acquired

images, consists in solving the correspondence problem,

then computing the ray intersection.

CSE668 Sp2011 02-24

---

Computing the ray intersection

To recover the world coordinates Xw of a point from

ul~ and ur~ corresponding to the same scene point X,

remember that the image affine coords and the camera

coords are related through the camera calibration

matrix K by the expression we derived last time

            z_c [u v 1]^T = K [x_c y_c z_c]^T

Assuming the focal distance f, scale factors a and c

are all nonzero, then K is invertible and

[x_c/z_c y_c/z_c 1]^T = K^-1 [u v 1]^T

So the ray corresponding to the image point (u,v)

can be expressed in camera coordinates as

        a K^-1 [u v 1]^T for all a>0.

CSE668 Sp2011 02-25

---

But since in general world and camera coords satisfy

        X_c = R(X_w-t)

with R the rotation matrix and t the translation vector,

        X_w = R^-1X_c+t

and we can express the ray in world coords as

a R^-1 K^-1 [u v 1]^T  + t  for all a>0

CSE668 Sp2011 02-26

---

Now suppose we have u_l~ = [u_l v_l 1], u_r~ = [u_r v_r 1]

which correpond to the same scene point X, and we have

the corresponding left and right camera models. Then in

world coords, from the left image, the scene point X_w

satisfies, for some a_l>0,

    X_w =  a_l R_l^-1 K_l^-1 [u_l v_l 1]^T  + t_l

while from the right image,

    X_w =  a_r R_r^-1 K_r^-1 [u_r v_r 1]^T  + t_r

But the world coords as viewed by the two cameras

must agree, since we are considering the same point

in the scene. So equating the RHS's of the last two

expressions, we can solve for the ray a-parameters

and thus for Xw. There are actually three scalar

equations in two unknowns a_l and a_r but since the

two rays must be coplanar, this system of equations

will be of rank two and have an unique solution.

CSE668 Sp2011 02-27

---

Eg:

    Identical cameras K_l=K_r= identity matrix I (implies

    b=u_o=v_o=0 and f*a=f*c=1). Lets make the world and left

    camera coords the same, so t_l=[0 0 0]^T, R_l=I. Right

    camera is translated one unit to right t_r=[1 0 0]^T

    of left camera and rotated 30^o ccw in the x-z plane,

    R_r = [cos30^o 0 -sin30^o; 0 1 0; sin30^o 0 cos30^o].

CSE668 Sp2011 02-28

---

    Suppose with this setup, we find a correspondence

    between image points (u_l,v_l)=(1.20,-0.402) and

    (u_r,v_r)=(0.196, -0.309). What is the corresponding

    scene point X in world coords in R³?

        Xw =  a_l R_l^-1 K_l^-1 [u_l v_l 1]^T  + t_l =

a_r R_r^-1 K_r^-1 [u_r v_r 1]^T  + t_r

    Plugging in the K's and t's and equating the last two,

a_l [u_l v_l 1]^T = a_r R_r^-1 [u_r v_r 1]^T  + [1 0 0]^T

    and then the rest of the parameters and image points,

a_l[1.20 -.402 1]^T - a_r[.670 -.309 .768]^T = [1 0 0]^T

CSE668 Sp2011 02-29

---

    ^{Easiest way to solve is to look at top two equations}

[1.20 -.670; -.402 .309] [a_l a_r]^T = [1 0]^T

    which yields a_l= 3.05, a_r = 3.97. Plugging back,

    from the left image the scene point must be

        Xw = a_l [u_l v_l 1]^T = 3.05 [ 1.20 -0.402 1 ]^T

           = [3.66 -1.23 3.05]

    while from the right image it is

        Xw = 3.97 R_r^-1 [0.196 -0.309 1]^T  + [1 0 0]^T

           = [3.66 -1.23 3.05]

    The left and right images agree as to the location in

    world coords of the scene point. Note also that the

    third equation is indeed also satisfied by the solution

    we have found:

a_l - .768 a_r = 3.05 - .768*3.97 = 0

CSE668 Sp2011 02-30

---

Epipoles and epipolar lines

As seen above, once the correspondence problem has

been solved, its easy enough to determine the world

coordinates. In general, given a point in the left

image, it requires a 2-D search to find the

corresponding point in the right image. This can be

reduced to a 1-D search through the use of epipolar

geometry.

CSE668 Sp2011 02-31

---

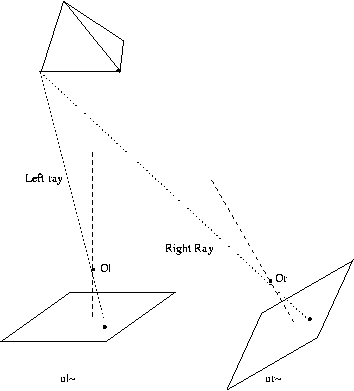
Let C and C' be the centers (focal points) of the

left and right cameras. We will draw the image plane

in front of C, rather than behind it where the image

is inverted, for clarity.

The line of centers CC' is called the baseline of the

stereo camera system. The points where the baselines

intersect the image planes are called the epipoles

e and e'.

For any scene point X, the triangle XCC' cuts through

the image planes in two lines ue and u'e' called the

epipolar lines.

CSE668 Sp2011 02-32

---

Here's the point. Suppose we identify a point u in the

left image corresponding to a scene point X. Then u

together with the epipoles e and e' define a plane.

Where might X be in R3? Anywhere along the ray Cu,

which lies entirely in that plane.

But note that as X occupies different positions along

Cu, it remains in the plane, and the corresponding point

u' in the right image remains on the epipolar line u'e'.

So the correspondence problem is solved by a 1-D search

over the epipolar line.

Eg:

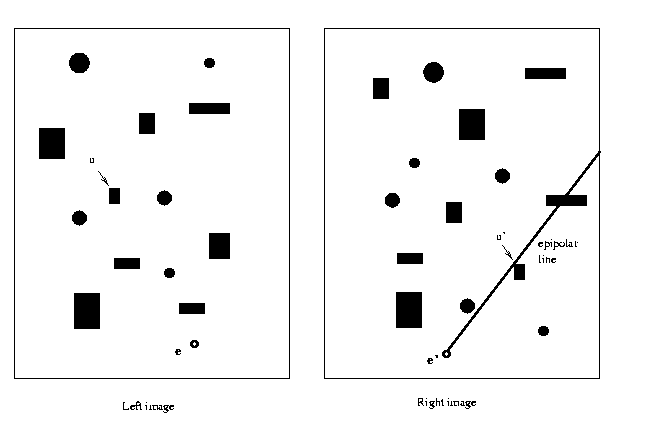
CSE668 Sp2011 02-33

---

The epipolar line is often computed from the fundamental

matrix F, where

        F = K^-T S(t) R^-1 K'^-1

and

            K, K': the left and right camera matrices;

            S(t): a matrix determined by t = C'-C;

            R: the rotation matrix of the right camera

               relative to the left camera

(see Sonka p 462)

via the Longuet-Higgins equation

            u^T F u' = 0

If say u' is specified, then with the point (row vector)

u^T having homogeneous coordinates [u v 1]^T, the L-H equation

is a single scalar equation in 2 unknowns which defines a

line in the image plane, the epipolar line.

CSE668 Sp2011 02-34

---