CSE668 Lecture Slides Spring 2011
7. Passive 3-D Object Recognition
We
will now return from our foray into low level
active vision (Sections 5-6 of these notes) to complete
our discussion of the standard (passive) paradigm
approaches to 3-D and motion vision begun in Sec
2-3.
These are the higher level passive operations,
more
AI-dependent, as opposed to the lower level
passive
operations such as stereopsis, more signal
processing
dependent, which we have discussed thus
far.
Required reading: Sonka, Ch.
10.
Most of our presentation of 3-D OR
will be descriptive
rather than
analytic. That is, we will not
go into
detail
concerning the representations and algorithms. The
only
exceptions will be in the goad algorithm and the aspect
graph
method,
both
of
which
will be discussed towards the
end
of this section.
CSE668 Sp2011 Peter Scott 04-00
In our consideration of Shape Recovery in Sec. 3,
we saw that the paradigm of "vision-for-recovery"
is very ambitious and in most general cases the
results
have been limited and perhaps disappointing.
Here we consider a somewhat less ambitious, though
still very difficult, task: 3-D Object Recognition
(OR).
It is easier than shape recovery because you
do not have to recover an object in order to recognize
it.
Eg: You can recognize an object as "a ball" without
recovering
its
full
details:
surface
texture,
exact
shape, size, etc.
CSE668 Sp2011 Peter Scott 04-01
Suppose there are m hypotheses (object classes) in
the Frame Of Discernment (FOD), the set of all object
classes you can declare. OR is the association of
an object from the scene with a hypothesis 1...m from
the frame of discernment, ie. declaration of one class
label
as the true hypothesis.
Typically ("open system assumption"), one of the hypotheses
is
called the null hypothesis, the
hypothesis that states
that the object
does not
belong to any of the other m-1
classes. In a
closed
system the null hypothesis is not
included and it
is assumed all objects in the scene can be
correctly associated with one (or more) of the hypotheses.
CSE668 Sp2011 Peter Scott 04-02
Distinct hypotheses may require physically distinct
object classes, such as class 1: vehicles, class 2:
people, class 3: clouds, etc. Or the hypotheses may
be combinations of object physical characteristics
and
other properties.
Eg: FOD = { people facing camera, people facing
away from camera, animals moving, animals stationary,
null hypothesis }
CSE668 Sp2011 Peter Scott 04-03
How are objects declared to belong to class i
rather than class j? OR always involves comparisons.
These
comparisons may be of two general types:
1. Comparing descriptions
of the object features
with features of archetype objects of each class;
2. Comparing object class construction rules
with the manner in which the object to be
recognized
may
be
constructed.
CSE668 Sp2011 Peter Scott 04-04
The first is called recognition by analysis in which
features of the object are matched against features
of each of the stored archetypes (except the null
hypothesis), and the best match, if it is above a
preset threshold, determines the classification decision.
If
no class matches sufficiently, and the null hypothesis
is available (open-world assumption), the null hypothesis
is
chosen.
Eg: FOD = {vehicles, buildings, null hypothesis}.
A car would be classed a vehicle since there
would be an archetype with similar features:
four wheels, similar size, windows, etc.
CSE668 Sp2011 Peter Scott 04-05
The second is called recognition by synthesis in
which the constructive procedures for each class
and the object are compared. Again, the best match
determies
the classification decision.
Eg. Syntactic recognition: reduce the object
to a string of symbols that represents a
constructive procedure for generating it. See
if that string is "grammatical" in the grammars
that represent each hypothesis (object class).
In
other words, see if it obeys the rules for
construction which define each class separately.
In either case, to make the comparisions we need
to
have data concerning the object and data
concerning
objects representative of each class
in
the frame of discernment to compare.
CSE668 Sp2011 Peter Scott 04-06
Describing
3-D shapes
Descriptions can be complete or partial. 3-D
recovery
is complete description,
ie.
a
different
description
for each
distinct object. Complete
descriptions
are also
called representations.
Eg: (x,y,z) for each surface point is complete.
Eg: (p,q) for each surface point is complete.
Eg: Polygonal approximations are incomplete.
Eg: Superquadrics are incomplete.
CSE668 Sp2011 Peter Scott 04-07
For 3-D OR we seldom work with complete
descriptions,
for several reasons:
1. Limited view angles and image sets;
2. Hard to compute;
3. Contain more detail than needed for
OR
matching.
Instead, we work with partial representations,
ie. models. Typically, we select a class of models
and within this class find the parameter values
(features) that best describe the object and that
best describe the archetypes. These feature vectors
may
then be matched.
Models
are never complete, ie. many distinct objects
are
represented by the same model. Models represent
classes of objects. But often models are
unique (each object has unique best model fit).
Unique
models are a well suited for OR use.
CSE668 Sp2011 Peter Scott 04-08
Volumetric (space-filling) models
Consider a discrete binary image. Each pixel has
2 possible values: true (white, background) and
false (black, object). Similarly, we may
define a discrete binary 3-D scene model which
consists of a grid of voxels, or volume elements).
If voxel (i,j,k)=0 that means that the corresponding
small spatial cube is filled by object rather than
background.
Eg: Voxel representation of a tetrahedron.
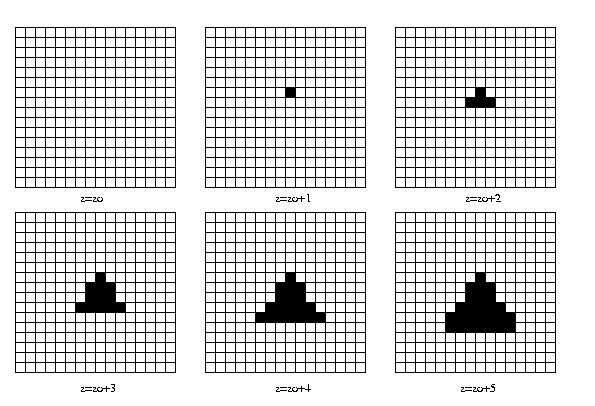
For
finite voxel size, since many distinct objects
have
the same "staircased" appearance, this creates
a
partial resentation, or model of the object. In
the limit, as the voxel size->0, voxel models become
complete representations. Voxel models come
with all the analytical tools of signal processing.
They tend to be high-dimensional, require lots of
storage,
particularly non-binary voxel models.
CSE668 Sp2011 Peter Scott 04-09
Volume
primitives
approach
Another way to fill space is with unions and
intersections of volume primitives, simple 3-D
solids. By using smooth-surfaced primitives such
as spheres and ellipsoids, or non-right-angle
primitives such as parallelograms and pyramids,
the 3-D staircasing in voxel models can be
avoided. Different classes of volume primitives
may
be employed.
Note that voxels are cubic volume primitives
which are combined through union to form space-
filling models, so voxel modelling is a special
case of the volume primitive approach.
CSE668 Sp2011 Peter Scott 04-10
Polyhedral
models
The
single volume primitive used to create 3-D
polyhedral
models is the half-space, ie. the
set of points x
in R3 satisfying
αTX+β≥0
for some α in R3
and scalar β. Only
intersections
of them are
required for convex
objects. General
non-convex
objects can be decomposed
into a union
of convex
parts, and so can
be modeled by unions
of such
intersected half-spaces.
One nice feature of polyhedral models is that
they can be characterized by 4 scalars
(a,b,c,d) for each facet (bounding plane),
since ax + by + cz + d ≥ 0 defines a half-space.
Another is that linear programming can be used
to determine vertices and characteristics.
The obvious weak point of polyhedral modelling
is the proliferation of artificial facet edges
vertices.
CSE668 Sp2011 Peter Scott 04-11
Eg: Polyhedral model of teapot, simple shading.

Source:
http://www.frontiernet.net/~imaging/fo_arch.html
CSE668 Sp2011 Peter Scott 04-11a
Eg: Polyhedral model of a bust of Beethoven
postprocessed with non-Lambertian surface
model and spot illumination.

Source: http://www.frontiernet.net/~imaging/fo_arch.html
Some kind of smoothing is obviously necessary
to make the model reasonably realistic
and
accurate.
CSE668 Sp2011 Peter Scott 04-11b
Constructive
geometry
models
The volume primitives are (typically) sphere,
cylinder, cone, cuboid (or prism) and half-space.
Sometimes ellipsoids, paraboloids and other
simple
forms
are
added
to
the
set
of primitives.
These models are surprisingly expressive, but it
is often difficult to determine the smallest set
for a given permissible deviation. The expressiveness
of a modeling scheme is the range of different
types of objects which it can accurately represent.
CSE668 Sp2011 Peter Scott 04-12
Super-quadrics
Quadric solids are defined by
ax2 + by2 + cz = d (Type I
quadric)
or
ax2 + by 2 + cz2 = d (Type
II quadric)
For instance if a and b are of the same
sign then the Type I quadric is called a
paraboloid, else a hyperbolic paraboloid.
If a, b, c and d are all of the same sign
then the Type II quadric is called an
ellipsoid.
CSE668 Sp2011 Peter Scott 04-13
Superquadrics are generalizations of quadrics
with additional parameters to make them less
smooth and symmetric than quadrics. See Sonka
Fig. 10-14 p 526 for some super-ellipsoids.
But note errors in exponent s in eqn 10-23
p
525. Should read
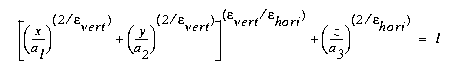
CSE668 Sp2011 Peter Scott 04-13a
A description of superquadrics and development
of some of their mathematical properties can
be found here. Superquadrics have many interesting
mathematical properties, and may be usefully
generalized in
various ways. They are much more
expressive than
quadrics, at the cost of two
additional
parameters (6 vs. 4) in the models.
CSE668 Sp2011 Peter Scott 04-13b
Sweep
representations
Given a 3-D object and a curvilinear path or
"spine" entirely contained within it, the object
may be described by defining at each point along
the spine the 2-D shape of the crossection of the
object at that point. This is called a sweep
representation, or generalized cylindrical
representation.
CSE668 Sp2011 Peter Scott 04-14
Eg: If the spine is a straight line in 3-D, and
the crossection is a circle with linearly
decreasing radius, the figure swept out is a
cone.
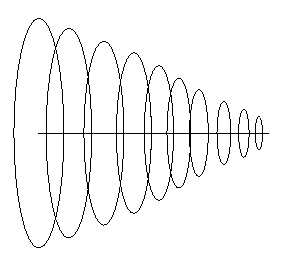
Sweep-represented objects need not have axes of
symmetry, or any symmetry whatsoever. But they
work best for "spaghetti-like" objects, that is,
objects for which the change in the crossection
for a properly selected spine is relatively slow
and smooth.
In case of hand-like objects with several
protruding parts, the spine must divide into
multiple skelelton like extensions. This
complicates
sweep representations significantly.
CSE668 Sp2011 Peter Scott 04-15
Surface
models
The alternative to space-filling models are those
that model the boundaries of the object: surface
models. Just as there are many ways to model
boundaries in 2-D, ie. 1-D curves on a plane,
there are many ways to model curvilinear 2-D
manifolds in
3-space.
There are two important problems to be solved in
computing a surface model: what class of manifolds
to use, and how and where they will intersect as
1-D curves in
3-D.
CSE668 Sp2011 Peter Scott 04-16
The simplest
volumetric model was the polyhedron, a
solid 3-D object with planar boundaries.
If we think of the elements of a polyhedron
model not as half-spaces but as the facets that
bound them, this model class can also be
considered a
surface model. However, if we are
describing a
polyhedron by quantifying its facets
we need to
specify its edges and vertices.
The edges
can be characterized by equating
pairs of
half-space boundaries, and the
vertices found
by solving
triples of these
equations.
CSE668 Sp2011 Peter Scott 04-16a
Eg: Consider the cube modelled volumetrically by
the
intersection
of
six
half-spaces
defined
by
the
inequalities
1x
+
0y
+
0z
>=
0
0x
+
1y
+
0z
>=
0
0x
+
0y
+
1z
>=
0
1x
+
0y
+
0z
<=
1
0x
+
1y
+
0z
<=
1
0x
+
0y
+
1z
<=
1
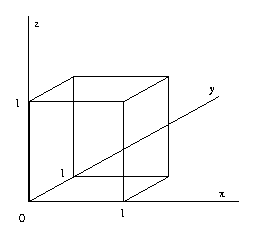
CSE668 Sp2011 Peter Scott 04-17
The half-space boundaries are these inequalities
considered
as
equalities
(e.g. x=0).
The
first
two
facets
intersect
where
x=0 and y=0,
which
is
the
1-D straight line
{
(x,y,z)
=
(0,0,z)
for
all
z
}
The
vertices
for
this
edge
between
facets
x=0
and
y=0
are
the points on all of the first three
half-space
boundaries
x=0,
y=0, z=0,
(x,y,z) = (0,0,0)
and the first two and the sixth,
(x,y,z) = (0,0,1)
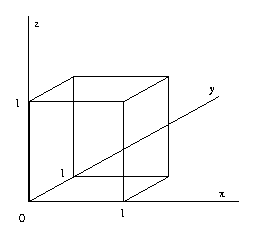
CSE668 Sp2011 Peter Scott 04-18
In this example, the 6 half-space inequalities
define the volumetric model, while the 6
corresponding equalities, together with the 12
edge equations and 8 vertices, define the
corresponding
polyhedral boundary model. Clearly,
the cube
requires more constraints to be described
as a surface
model than a volumetric model. But the
additional
boundary parameters in surface models
permit
modelling of non-convex
bodies, which cannot
be done with
intersections of half-spaces.
Eg: This object cannot be modelled using
intersections of half-spaces, but can be
using a surface polyhedral model.
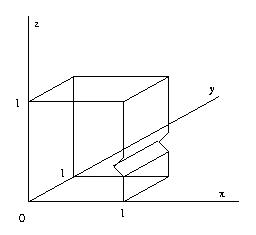
CSE668 Sp2011 Peter Scott 04-19
Delaunay
Triangulation
Given a set of
points on the surface of a 3-D object,
or surface point cloud, these points can be used as
the vertices of contiguous triangles whose union
models the surface of the object. This process is
called surface triangulation and the most common
stragegy is
Delaunay Triangulation:
1. Select 3 points from the point cloud and find
the unique circle they lie on. Extend that
circle to the unique sphere that has that
circle as a great circle.
2.
If
there
are
no
other
points
in the surface
point cloud which are in the interior
of that sphere, make these three points
vertices of a triangular facet of the model.
3.
Repeat
steps
1
and
2
for
all sets of 3 points.
CSE668 Sp2011 Peter Scott 04-20
A problem with the algorithm given above is that like
polyhedral volumetric modelling, it requires
additional constraints to handle non-convex objects.
The unconstrained algorithm above returns the convex
hull
of
the
point
cloud.
Eg:
given
the
vertices
of
the
non-convex
figure of 04-18
as
the
surface point
cloud,
unconstrained
Delaunay
Triangulation
will
return
the
cube shown in 04-19.
Delaunay Triangulation can also be extended to
non-convex objects by first decomposing the point
cloud into the union of point clouds in which the
convex hull models the object, then performing the
algorithm on each separately and merging the
resulting
convex
polyhedrons.
CSE668 Sp2011 Peter Scott 04-21
Eg:
This
non-convex
object
can
be
decomposed into
the union of two convex
objects by splitting
it vertically at z1.
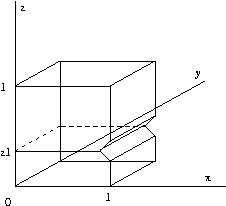
There are numerous other triangulation schemes (e.g. constrained
triangulation, Morse triangulation) but Delaunay Trainagulation
is still the most commonly used in practice.
CSE668 Sp2011
Peter Scott 04-21a
Object-based
OR
using
volumetric
or
surface
models
Having
considered
several
types
of
3-D models, we now
turn
to
the
question
of
how
are
we
to use a 3-D model
for
OR?
As
suggested
earlier,
general
pattern
recognition
procedures
most
often
have
these
steps:
A. Offline:
1.
Compute
one
or
more
archetype
models (ideal
noise and distortion free models) for
each class.
Call this the class library.
2. Precompile a set of attributes Ai for each
member of the class library. Ai will be
used for purposes of matching.
3. Precompile other properties of the class
library and the data environment which will
be of use online, such as thresholds and
probabilities.
CSE668 Sp2011 Peter Scott 04-22
B. Online:
1. Given the online data, compute model of the
object
to
be
classified,
including
the
value
of
its
attributes
A.
2. Initialize: make an initial guess hypothesis Hi.
3. Compute match score for current hypothesis Hi.
4. If match threshold exceeded, declare object
to
be
recognized
and
its
class
to
be class i,
else
make
another
hypothesis
and
go
to
3. If all
hypotheses
have
been
tried
declare
recognition
failure.
5. If a learning pattern recognition procedure,
update precompiled database in light of
experience.
CSE668 Sp2011 Peter Scott 04-23
By a hypothesis, we mean a declaration of the object
class, together with any necessary view parameters, ie.
a declaration of what we are looking at and and how we
are
looking
at
it.
Eg: In a 3-D object-centered OR system with unknown
illumination and scale, a hypothesis would be
an object class together with camera pose and
location
parameters
and
illumination
parameters.
Eg: In a 3-D view-centered OR system with fixed
pose and scale and illumination, a hypothesis
would be an object class together with a view
index
number
(eg.
this
is
view
17
of object 6).
CSE668 Sp2011 Peter Scott 04-24
In methods employing the recognition-by-analysis
approach, the "set of attributes" are quantitative
or categorical mappings from the model called features.
Note: a categorical mapping is a mapping into a
non-numerical set which need not be endowed with a
similarity
or
distance
metric.
Eg: The feature set {surface point, edge point,
vertex point} is categorical.
Eg: For a polyhedral surface model, we can take the
set of outward pointing normals and the locations
of the centroids of each facet as the features.
These
are
all
numerical
features.
Eg:
For
a
voxel
model,
we
can
take the (i,j) moments
for
0<=i,j<=M
as
the
(numerical)
features.
Eg: For a sweep representation model, we can take
length and curvature of the spine, together
with Fourier Descriptors of sampled crossections,
as
the
feature
vector.
CSE668 Sp2011 Peter Scott 04-25
Object-centered coordinate systems assume that the object
being viewed is located at the origin of the world coord
system (xw,yw,zw)=(0,0,0) and that it has a specific
known pose (3-D rotation relative to the world coord
axes).
Eg: If the distance to the origin of world coords
from the camera is known, each extrinsic camera
model can be represented as 3-D vector indicating
the direction of the camera coordinate z-axis
("optical axis" of the system) in world coords,
a point on a sphere indicating camera location,
and a 2-D rotation vector indicating the rotation
of
the
image
plane
in
camera
coordinates.
CSE668 Sp2011 Peter Scott 04-26
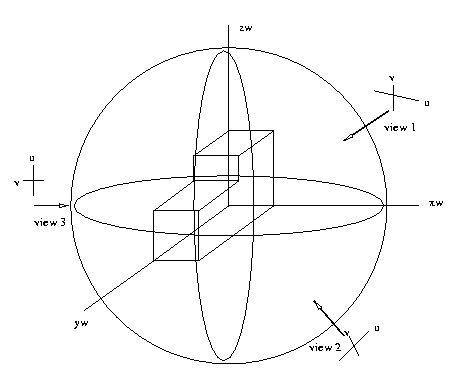
The canonical position of the object in world coords
is often taken to be such that a selected vertex is
at the origin as shown, or such that the centroid of
the object is at the origin. The canonical pose is
such that the major axes of the object are oriented
with the world coord axes, or principal edges are
aligned
as
much
as
possible.
CSE668 Sp2011 Peter Scott 04-27
The
Goad
algorithm
If we use 3-D polyhedral models, the Goad algorithm can
be
used
to
implement
the
OR
procedure.
Assume
the
class
library
consists
of
polyhedral
archetypes,
one for each class. Take the feature set for each member of
the class library to be the complete set of object edges,
each represented by an ordered pair of points in world
coords.
Eg: Object is an ellipsoid, polyhedral model has
8
facets,
6
vertices,
12
edges.
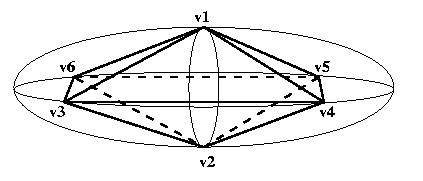
Then
e1=(v1,v3),
e2=(v1,v6),
...
e12=(v2,v4)
CSE668 Sp2011 Peter Scott 04-28
The camera is assumed to be a unit distance away from
the object to be classified, and records an image. That
image is precompiled to a polyhedral model and thence
to a set of edges (represented by pairs of vertices).
The location p on the unit sphere is not known, nor the
optical
axis,
nor
the
camera
image
plane
rotation
q.
The optical axis degree of freedom can be removed by
translating the object to the center of the image,
orienting the optical axis to the world coord
origin.
Thus, a hypothesis will consist of an object class
together with (p,q), the view location and image
plane rotation extrinsic camera parameters.
Note: Do not
confuse the 3-D location vector p and
2-D rotation
vector q here with the scalar components
(p,q)
of
the
gradient
space
defined
for
shape
recovery.
CSE668 Sp2011 Peter Scott 04-29
The
standard
form
of
Goad's algorithm assumes the object
is
opaque.
Thus,
given
view sphere location p, we must
consider
that
only
some
edges will be visible.
The set
of
p's
from
which
a given edge
e
is
visible
is called
the
visibility
locus of e, and denoted L(e).
Eg: for the p shown in 04-28, edges (v5,v6), (v2,v6)
and
(v2,v5)
will
not
be
visible.
So
this p is
not
in
L(v5,v6), L(v2,v6) or L(v2,v5).
The basic idea
of Goad's algorithm is to seek an object
label, p and q for which edges in the object image and
edges in an image computed from the class library match
up
as
much
as
possible
for
p
in
L(e).
CSE668 Sp2011 Peter Scott 04-29a
The algorithm proceeds by hypothesize-and-verify over
increasing
edge
sets
with
backtracking. At a given iteration,
we
have
our
current
hypothesis (ωi,
p,
q)
where ωi is the
hypothesized
object
class,
and a the set
of edges
that
we
have
matched
with
this
hypothesis
up to this iteration. We
select
an
unmatched
edge
in
the
object
image, and based on
the
intersections
of
L(e)
for
all
matched
edges,
determine
a region where the matching edge must lie in the (ωi, p, q)
pre-stored
image.
If
there
is
one
there,
we
have
verified
the hypothesis so
far,
and
we
continue
by
seeking
to
match another edge
that
has
not
yet
been
matched.
If there fails to be one, ie. no edge in the (ωi,
p,
q)
pre-stored
image
which
is
in the intersections
of
L(e)
for
matched
edges,
the
hypothesis
(ωi,
p,
q) is rejected
and
we
backtrack
through
(p,q) space.
CSE668 Sp2011 Peter Scott 04-29b
The
algorithm
terminates
with
success when there are no
unmatched
edges
in
the
object
image,
and
the
current
hypothesis
(ωi,
p,
q)is declared. It
terminates
in
failure
when
we
have
backtracked
through
all
(ωi,
p,
q) for
the
current
ωi.
In
this
case the object is not
of
class
ωi,
and
we
move
on
to the next
class.
Note
that
since
there
are a finite number of hypotheses, and
each
polyhedral
object
image
has a finite number of edges, the
algorithm
has
guaranteed
convergence.
CSE668 Sp2011 Peter Scott 04-30
2-D
view-based methods
There are 3 distinct strategies we can employ for
matching
in
a
3-D
OR
problem:
1. 3-D model-based matching: the library stores
3-D archetypes. The image object is recovered, ie.
a 3-D model is produced, and the size, position and
pose of the image object relative to the archetype
are
hypothesized.
Matching
is
done
in
R3.
2. Hybrid matching: the library stores 3-D archetypes.
Based on the 2-D view (image), but without recovery,
the pose, size and location are hypothesized and
used to create a synthetic view. Matching is done
in R2. Goad's algorithm is an example of hybrid
matching.
CSE668 Sp2011 Peter Scott 04-31
Full 3-D model-based matching is seldom attempted
for practical applications except in very narrow
domains (eg. blocks-world type). Problem is the
difficulty
with
recovery.
Hybrid matching is sometimes used for non-time-
critical applications.
There is a way to implement 2-D matching which does
not require creating synthetic views online,
in
which
a
set
of
such
views
are
precompiled.
3. 2-D view-based matching: the library stores a set
of 2-D views of the object. Based on the 2-D image
object, the best stored 2-D view is selected and
matching is done in R2. This is the kind of matching
we saw earlier with the Nelson homing algorithm. In
that case the entire scene, not just an object in
the scene, was matched.
CSE668 Sp2011 Peter Scott 04-32
To perform view interpolation, that is, the rendering of
a synthetic view from a view location which has not been
stored, an important fact is that a given object point
in one view may be mapped into its location in another
view using a simple transformation (affine in case of
orthographic projection, trilinear in perspective
projection). This can permit "tuning" the view location
before matching as long as the set of visible object
points
has
not
changed
between
views.
Eg:
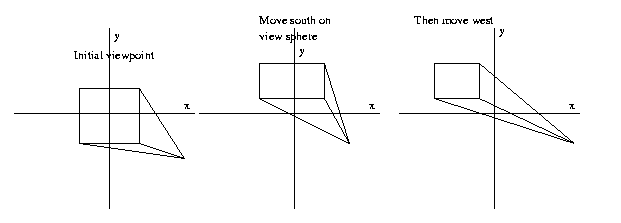
Note
that
only
edges
and
vertices
visible
in
a given
image
can
be
mapped
using
such
methods.
Features
visible
from
an
unstored
pose
but
not
visible
from
a stored pose
will
be
missed
in
the
"tuned"
image.
CSE668 Sp2011 Peter Scott 04-33
Most of the work on view-centric approaches assumes
that the object models are polyhedral, both library
views and object views. Polyhedra have many nice
properties
for
relating
views
around
the
view
sphere.
1. They can be easily characterized in a given
view by sets of vertices and edges;
2. Polyhedral edges are straight in any view;
3. For most small changes of viewpoint, there is
no
change
in
the
set
of
visible
object points.
CSE668 Sp2011 Peter Scott 04-34
If the 3-D polyhedron is convex, then there is a
fourth
important
simplifying
property:
4. Either an entire edge and both its terminating
vertices are visible, one of its two vertices
and none of the edge interior is visible, or
no part of the edge is visible.
Eg:
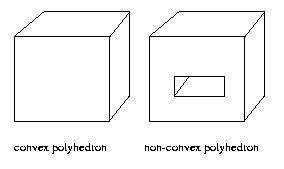
Note that a view of a non-convex polyhedron may contain
"false vertices," that is, vertices of the view that
do
not
correspond
to
object
vertices.
CSE668 Sp2011 Peter Scott 04-35
The most direct approach to 2-D view-based OR would be
to store views equally spaced around the view sphere.
For instance, the centers of the 20 triangular facets
of the icosahedron. Or, if a greater set was desired,
dividing each of these 20 triangles into 4 triangles
whose vertices are the original triangle vertices plus
the
midpoints
of
the
three
sides.
A problem with such a method is that equal sized view
loci may over-model certain aspects of the object and
under-model others, making reliable recognition hard
or
impossible.
CSE668 Sp2011 Peter Scott 04-36
Eg:

Consider the union of the view loci of the two
vertices at the bottom of the slot. If there is
not a viewpoint on the view sphere in that union,
we would get no information about the structure
of the bottom of the slot. That union would be
a small proportion of the surface area of the
view sphere, so having a viewpoint in there would
not be very likely. Then, if there were two object
classes that differed only in what's going on in
that slot, we could never distinguish them since
their
set
of
stored
views
would
be
identical.
CSE668 Sp2011 Peter Scott 04-37
Characteristic
views
In the late 1970's and early 1980's groups led by
J.K. Koenderink and H. Freeman developed the ideas
of the characteristic views and the aspect graph.
These ideas have made 2-D view-centric approaches
the dominant
choice for 3-D OR ever since.
Let us limit ourselves to employing polyhedral
models. Any
view of a polyhedral model, either
perspective or orthographic, reduced to a line drawing,
is called an aspect of the model. An aspect is
identified
(uniquely specified) by
the set of its
visible facets.
Two aspects are said to be
adjacent if they
differ by
only a single
facet. A
nondirected graph in which the
aspects are
nodes and
two aspects are connected by an
edge iff they
are
adjacent views is called an aspect
graph.
CSE668 Sp2011 Peter Scott 04-38
Every view of a given object always has both
topological
and geometric characteristics.
Topological: graph structure of the view when
considered
as
an
undirected
graph
(Image
Structure
Graph ISG), ie. number of vertices and
their
interconnectivity.
Geometrical: lengths of
edges, size of angles.
Call a view "stable" if a small neighborhood around
the viewpoint contains only views with the same
topological
structure, ie. where the same aspect is
viewed. Then a
contiguous stable set of views
bounded
by unstable
viewpoints is called a characteristic
view
domain, and
the aspect being viewed in that domain is
called a characteristic view.
A characteristic view
class
is a set of characteristic view
domains which
are topologically equivalent, ie. have identical
ISGs.
CSE668 Sp2011 Peter Scott 04-39
Eg: For a cube, there are 26 characteristic view
domains
and
3
characteristic
view
classes.
The
3 ISGs corresponding to these 3 classes are
completely
connected
graphs
with
1,
2
and
3 nodes.
For convex polyhedra, the characteristic view
locus boundaries correspond to view loci formed by
the facets of the polyhedron projected onto the view
sphere.
CSE668 Sp2011 Peter Scott 04-40
To determine the aspect graph for a convex polyhedral
object, extend the facets to complete planes in
R3, and note how they planes partition R3 into
cells. All cell
boundaries are planes. Each cell
except the
object itself corresponds to an aspect
of
the polyhedron.
The nodes in the aspect graph are the aspects of the
polyhedron. Aspects are adjacent if they are
connected by a cell face. Each pair of adjacent
aspects are connected by an edge in the aspect graph.
That completes the definition of the aspect graph for
polyhedra.
CSE668 Sp2011 Peter Scott 04-41
Eg: Construct
the aspect graph of an elongated cube.
Begin
by
extending
each
object
facets
into
a full plane.
For an elongated cube, there are six facets which
partition R3 into 27 parts, one occupied by
the object itself, leaving 26 aspects.
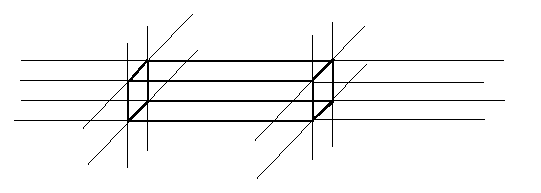
Let's
number
the
aspects,
beginning
with
the
nine
aspects above the object. Starting from the
left and backmost aspect, lets number them in
raster order looking down at the object. Continue
in that fashion for the eight aspects neither
above nor below the object, then the nine below.
So for instance aspect 2 is above and behind,
while aspect 14 is directly to the right of
the
object.
CSE668 Sp2011 Peter Scott 04-42
Let's also number the object facets. Call the
one nearest to us facet 1, facet 2 to its right,
facet 3 behind, facet 4 to its left, 5 above,
6
below.
We are ready to construct the aspect graph. It
will have 26 nodes, each labelled by a line
drawing of the object as seen from that aspect.
Each of the extended planes has 8 cell faces
connecting
aspects,
for
a
total
of
48
edges.
CSE668 Sp2011 Peter Scott 04-43
For
instance,
aspect
1
looks
like
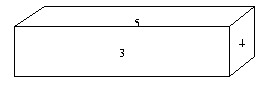
and has edges connecting this node to aspects
number 2, 4 and 10. So this part of the aspect
graph
would
look
like

Note that he aspect graph nodes do not need to
contain
line
drawings,
they
are
just
shown
here for
illustrative
purposes.
CSE668 Sp2011 Peter Scott 04-44
For a typical example, many of the aspects are
topolog-
ically equivalent. That is, if we made an ISG of each
aspect, in which the visible facets were nodes
and adjacent facets were connected with edges
these
ISGs
would
be
isomorphic.
For our example, there are only 3 topologically
distinct
aspects,
ie.
3
non-isomorphic
aspect-top-
ology graphs: 1-facet, 2-facets, 3-facets, and
thus three characteristic views.
CSE668 Sp2011 Peter Scott 04-45
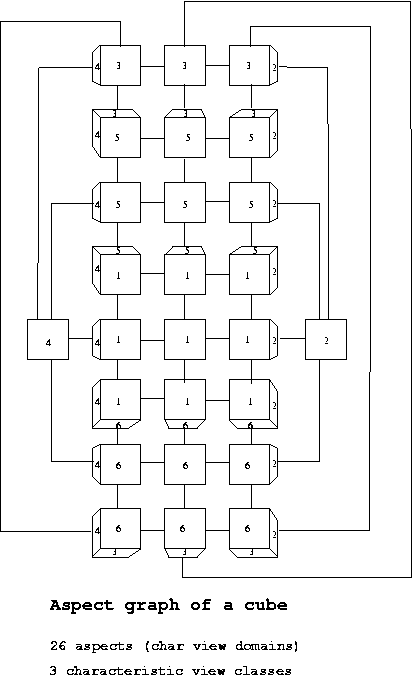
CSE668 Sp2011 Peter Scott 04-45a
Adjacent views,
those
linked in the aspect graph,
have the
property
that there is a continuous path
of stable view
locations
connecting them. That is,
a viewer can
move
from one aspect to the other
without
encountering
any other aspects, and do so
even with small
perturbations
to the path. Thus
no single-facet
view
is linked to a 3-facet view,
since in moving
from
a one-facet view, one of the
two additional
facets
would be encountered first,
to first see
them
both at exactly the same point
in the path is
unstable.
CSE668 Sp2011 Peter Scott 04-45b
Construction of the aspect graph for non-convex
polyhedra is more difficult. Freeman calls the
partitioning planes described so far type A planes.
There are type B planes formed by an edge and a
non-adjacent vertex, sometimes called edge-vertex
planes.
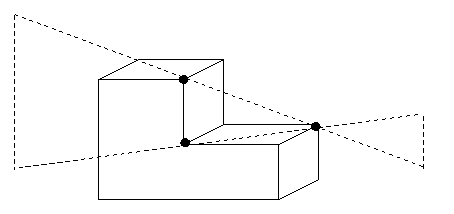
Type B plane
And in certain
complex cases involving non-convex
polyhedra there
are type C surfaces, which
are not
planes but
piecewise planar "ruled
surfaces." For
more detail,
see Wang and Freeman's
paper in H.
Freeman (ed.),
"Machine vision for 3-D
scenes,"
Academic Press
1990.
CSE668 Sp2011 Peter Scott 04-46
The Aspect Graph Match Method for 3-D OR
Aspect graphs are used in 3-D OR by segmenting out
the object to be recognized from the image, mapping
it into a 2-D
polyhedron (ie. an aspect) and thence to
an Image
Structure
Graph (ISG). The ISG is an undirected
unattributed
graph
in which the nodes of the graph are
the vertices of
the
aspect, and the links are its edges.
We look for a match with ISGs of the aspects of
each class aspect graph.
If there are one or more matches to aspects within
a single aspect graph, a recognition is declared. If
no matches
anywhere, the null hypothesis is declared.
If there are matches in two or more aspect graphs,
a second view can be taken from an adjacent viewing
position and the process repeated. Candidate classes
must have aspects that match both views, with an edge
in the aspect
graph between them.
The process is
continued until all matching aspect graphs
have been
found. If none, declare OR failure (null hypothesis).
If one or more, proceed to geometric matching step. Aspect
graph matching
does not consider geometry.
CSE668 Sp2011 Peter Scott 04-47
Note:
There is a graph related to the ISG called the Planar
Structure Graph.
The
nodes
of
the
PSG
are
the
visible vertices
of the object,
the edges are its visible edges. While any two
aspects which
are topologically equivalent have the same PSG's,
two aspects can
have the same PSG's without being topologically
equivalent (the
same is not true of ISG's).
Eg:
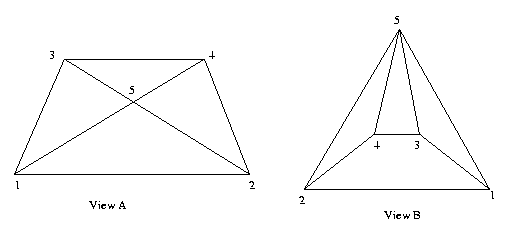
These
two
views
are
not
topologically
equivalent
even
though their PSGs are identical:
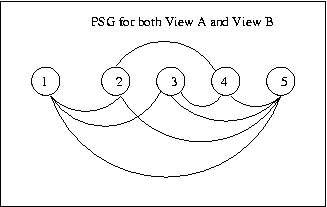
To be
topologically equivalent, two views need to
have isomorphic PSGs and be related by rotation,
translation and
perspective projection in R3.
CSE668 Sp2011 Peter Scott 04-48
Finally, note
that views that match topographically
(perfectly
matching aspect graphs)need not match
geometrically.
So a final step must be done after
topographic aspect graph matching to determine if
the object view
geometries match up as well. Thus
we should check
for matches in angles and proportions.
Eg:
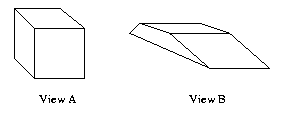
The topologies of these views match but not their
geometries. There is no 3-D polyhedron such that
Views
A
and
B
are
both
views
of that object.
CSE668 Sp2011 Peter Scott 04-49
Batlle
on
natural
object
OR
from
outdoor
scenes
Required
reading: Batlle et al, A
review on strategies
for recognizing
natural objects in color images of outdoor
scenes, Image and Vision
Computing
v18 (2000) 515-530.
We close our look at 3-D OR with a general
review of OR constrained to an important problem domain:
recognizing
objects in unstructured outdoor scenes.
This is a typical 3-D domain: it is constrained
in terms of object classes, but there is great
variability in the appearance of objects. The
number of object classes in the 20 or so systems
surveyed ranged up to 14. Typical: {bushes,car,
fence,grass,road,roof,shadow,window}.
CSE668 Sp2011 Peter Scott 04-50
Outdoor scenes
are challenging because the appearance
can change radically in seconds due to cloud movement.
In such circumstances, color is very important for
segmentation,
and all the systems tested use color.
Natural objects tend to have complex and highly
variable shapes that make them poor candidates
for accurate shape modelling (eg. trees, rocks,
grass) whether 2-D view-based or 3-D object-based.
Most frequently they are modelled by a feature
vector capturing a few coarse shape descriptors
(eg. aspect ratio, major axis) together with
texture and
color features.
An important part of OR in such scenes is adjacency
rules: for instance, the sky cannot be under a rock,
or a rock high in a tree. This is an example of the
use of object
relationship or context rules
in OR.
CSE668 Sp2011 Peter Scott 04-51
The surveyed
algorithms are of three basic types:
top-down,
bottom-up and hybrid.
Top-down: begin with a small set of hypotheses,
employ hypothesize-and-verify to aid segmentation.
Use heterogeneous knowledge-based procedures such
as context rules and object-part rules for
both
segmentation and matching.
Bottom-up: begin with pixel values, use data-driven
procedures, uniform classes of archetype models and
image object models. Only hypothesize at final
matching step.
Hybrid: do some bottom-up processing (eg. non-
purposive low-level segmentation), then top-down
processing (eg. class-specific merging high-level
segmentation
rules).
CSE668 Sp2011 Peter Scott 04-52
Top-down
systems can
handle very complex scenes
due to their flexibility, different procedures for
different hypotheses. But they are not good at
handling or learning unmodelled objects, or where
there are many
object classes.
Bottom-up systems can handle unmodelled objects well,
since they generate descriptions of all objects
encountered, not just objects of known classes. But
they have great difficulty with complex scenes and
are mostly limited in practical use to "blocks-world"
type problems.
Hybrid systems combine the discrimination power of
top-down systems with the robustness of bottom-up
systems. After initial non-purposive segmentation,
the segments and their adjacencies can be used to
order hypotheses for purposive continuations. The
descriptions derived for new classes can be the
basis for
learning.
CSE668 Sp2011 Peter Scott 04-53
Main takeaway from Batlle's paper:
current computer vision
systems working in
natural (not artificially
constrained)
outdoor environments
are not yet capable of
recognizing lexicons
of hundreds or thousands of distinct
object types reliably. Small
lexicons can be
handled, but the scale-up problem
has not yet been
solved.
There has been some progress in natural scene labelling
since the
paper was written in 2000, but I think the
conclusion is still valid.
CSE668 Sp2011 Peter Scott 04-54