CSE668 Principles of Animate Vision Spring 2011

9. Vision for recognition

Required reading:

1. Nelson, From visual homing to object recognition,

in Aloimonos (ed.) Visual Navigation, Lawrence Erlbaum

Associates, 1997. This paper was passed out previously.

2. Borotschnig, Appearance-based object recognition,

Image and Vision Computing v18 2000.

CSE668 Sp2011 Peter Scott 09-01

---

In the Fermuller-Aloimonos Active Vision Paradigm

heirarchy of competencies, first comes the motion

competencies, then the shape competencies. Object

recognition is one of these.

Nelson presents a procedure for extending the

associative memory based approach he used for homing,

a motion competency, to OR. This is consistent with the

Active Vision Paradigm insistence that competencies

are layered on one another, dependent on one another.

This is where we will start our look at methods for

implementing shape competencies.

CSE668 Sp2011 Peter Scott 09-01a

---

Nelson's associative memory-based OR

There are two broad classes of 3-D OR methods:

    * Model or object-based 

    * Memory or view-based

Object-based methods use 3-D match criteria while

view-based methods use 2-D matching.

Earlier this semester we discussed examples of both

types: object-based methods based on volumetric,

polyhedral, superquadric and sweep representations.

the Goad algorithm. View-based methods included

the method of aspect graphs and characteristic

views. The Goad Algorithm is also view-based since

its match criteria are 2-D even though the stored

templates are 3-D.

CSE668 Sp2011 Peter Scott 09-02

---

In the spirit of active vision's emphasis on making

the link between percept (sensory data) and behavior as

direct as possible, Nelson chooses a memory-based

approach. In his view, we see then we act. The model

based approaches require an intermediate step of some

complexity: we see (2-D images) then we model (build a

3-D model for matching purposes) then we act.

Advantages of memory-based approaches:

    * Consistent with motion competencies;

    * Behavior rather than recovery oriented;

    * Less dependent on segmentation and pre-proc;

    * Faster online;

    * Consistent with learning;

    * OR becomes pattern recognition.

CSE668 Sp2011 Peter Scott 09-03

---

Some problems with memory-based approaches are:

    * Memory load;

    * Occlusion not easily handled;

    * Clutter not easily handled.

Nelson's two-stage associative memory approach is

meant to address all three of these problems.

The basic scheme involves these steps:

    Offline:

        1. For each training view of each object,

           determine and store the values of visible

higher level features called keys or key

features. The keys should be local rather

           than global.

        2. Over the entire training dataset, determine

           and store the relative frequency of association

           of each key with each hypothesis (object

           class, position, pose and scale).

CSE668 Sp2011 Peter Scott 09-04

---

    Online:

        1. Extract primitive features, combine into

           key features.

        2. Pass the key features through an associative

           memory designed to recall corresponding object

           classes and configurations (location and pose

           in image space).

        3. Add geometric information about the key

           features to produce the set of feasible

           hypotheses called the evidentiary set.

        4. Pass the evidentiary set through a second

           associative memory which associates each

           hypothesis with the evidentiary set using a

           voting procedure based on the probabilities.

So the first pass inputs the key features and outputs the 

evidentiary set, that is, narrows down the set of hypotheses

to be explored further to be only those which are realistically

possible given the keys and geometry, ie. the evidentiary set.

Then the second pass inputs these hypotheses and judges which

is most likely.

CSE668 Sp2011 Peter Scott 09-05

---

Here's how this procedure deals with the three main

problems with memory-based 3-D OR mentioned above:

    * Memory load: keys are semi-invariant, highly

      compressed object representations;

    * Occlusion: keys are local and the final OR decision will

      be based on a voting procedure not requiring a full view;

    * Clutter: voting procedures inherently tolerate

      feasible candidates with few votes.

Semi-invariance means that the key features change

only slowly as the pose and scale of the object changes

in image space. For instance, color of a given segment

of the object would be semi-invariant, while angle between

at a vertex would not be semi-invariant.

Note that this method is consistent with learning since

the probabilites can be adjusted as new training data

becomes available.

CSE668 Sp2011 Peter Scott 09-06

---

Eg: Trying to tell dogs from cats. We have an image,

    and find three key features in it. We pass each

    through the AM and find the first two are

    associated with a dog seen from two certain points

    on the viewsphere (poses), and the third with a cat

    in a different pose. Three feasible hypotheses

    are constructed, this is the evidentiary set:

    {(dog,configuration1),(dog,configuration2),

    (cat,configuration3)} where configuration=

    (location,pose). The geometry is used to estimate

    the distance of the animal, thus its location.

    These three are passed through the second-pass AM

    which tells us that the evidence is voting 2:1 for

    dog. That is the output of the procedure.

CSE668 Sp2011 Peter Scott 09-07

---

The intended mode of operation for the active vision

system is that the keys and probabilities of the keys

given the object class and configuration are determined

offline in advance. Online, the system takes a new

image and computes the votes for each of the feasible

hypotheses (the evidentiary set).

If the vote for the most likely hypothesis is not above

the decision threshold, another image is acquired and

the resulting votes combined. This process is repeated

until a winning feasible hypothesis is found, or until

no feasible hypothesis remains. In the latter case

object recognition failure is declared.

CSE668 Sp2011 Peter Scott 09-08

---

Implementation and tests

Nelson gives results for his method in a "toy"

environment, just as he did for homing. The goal is

to recognize children's blocks, seven simple polyhedral

objects: triangle, square, trapezoid, pentagon, hexagon,

plus sign, 5-pointed star. The background was uniform,

contrast was high and there was no clutter (except from

other blocks in certain experiments).

CSE668 Sp2011 Peter Scott 09-09

---

Two kinds of keys were tried: 3-chains and curve patches.

    * 3-chains: make polyline approximations to the

      the visible 3-D bounding contours. Combine 3

      touching line segments, characterize by its

      four vertices. Each such set of four vertices

      is a 3-chain. So each 3-chain feature is 8-D,

      the x-y image coordinates for each vertex.

    * curve patches: define the set of longest,

      strongest edges as base curves. For each, find

      the locations along the base curves where other

      nearby edges intersect them. Each such set of

      locations, together with the angle measures at

      the intersections, is a curve patch.

Note that both these classes of keys have the desired properties

of semi-invariance and locality of reference. They are semi-invariant

because small changes in viewpoint or image distortion only lead to

small changes in the feature values; they are local because they depend

only on the properties of a small region of the image.

CSE668 Sp2011 Peter Scott 09-09a

---

        Eg: curve patches on one edge of a six-sided non-convex
            polytope.

The feature vector for this curve patch would be 6D:

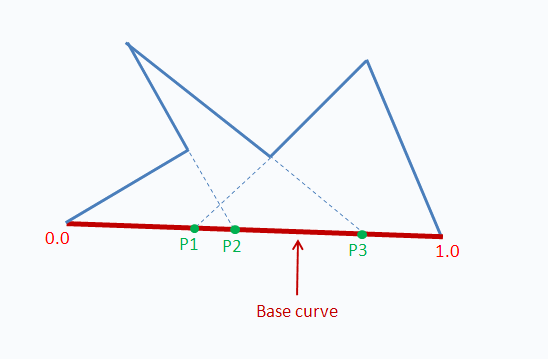
one location parameter in [0,1] and one angle measure

per point.

CSE668 Sp2011 Peter Scott 09-10

---

Online, the selected key feature set is computed from

the image and each key feature is associated with a set of

[object x configuration]-labelled images in the data base.

Hypotheses are formed (object x configuration x scale x 3-D

location) for each such association, and votes taken. For the

tests done in this paper, only a single view was used, that is,

evidence is accumulated over keys but not over views.

A set of training views was taken over approximately

a hemisphere of view angles, with variable numbers of

views for each object (max 60 for trapezoid, min 12

for hexagon).

CSE668 Sp2011 Peter Scott 09-11

---

Based on tests with a single visible object in the FOV,

Nelson approximates that his method is at least 90% accurate

(he claims no errors in the tests).

With one object and small portions of others, the

complete object was correctly recognized each time.

For objects with severe clutter and some occlusion

(presence of a robot end-effector in the FOV) the

results were significantly poorer (10%-25% in tests).

Nelson suggests the cause was poor low-level key extraction,

not memory cross-talk due to spurious keys produced

by the clutter.

CSE668 Sp2011 Peter Scott 09-12

---

As a final note, lets measure the Nelson approach

against the active vision and animate vision paradigms.

How would it score?

Active vision:

    * Vision is not recovery.

    * Vision is active, ie. current camera model selected

    in light of current state and goals.

    * Vision is embodied and goal-directed.

    * Representations and algorithms minimal for task

Animate vision: Anthropomorphic features emphasized, incl.

    * Binocularity

    * Fovea

    * Gaze control

    * Use fixation frames and indexical reference

CSE668 Sp2011 Peter Scott 09-13

---

Perhaps a C in terms of active vision, and a D for

animate. Nelson's approach perhaps strives for too

much universality across embodiments and tasks, and

does not incorporate the characteristics of human

vision sufficiently. It might be considered a

bridge between the old paradigm and the new.

CSE668 Sp2011 Peter Scott 09-14

---

Active object recognition

When we try to recognize objects that appear to

resemble several object classes, it is natural

to seek to view them first from one viewpoint,

and if this is not enough to disambiguate, choose

another viewpoint. An object recognition scheme

based on planning and executing a sequence of

changes in the camera parameters, and combining

the data from the several views, is called active

object recognition.

CSE668 Sp2011 Peter Scott 09-15

---

If the sequence of views is planned in advance and

followed regardless of the actual data received, this

is offline active object recognition. If we choose the

next camera parameters in light of the previous data

received, this is online active object recognition.

Eg: A robot with camera-in-hand moves to 4 preplanned

    positions and captures 4 views of a workpiece before

    a welding robot computes its welding trajectory.

Eg: A camera on a lunar rover sees something which

    may be a shadow or a crevasse. So it moves closer

    to get another look from a different groundplane

    approach angle.

CSE668 Sp2011 Peter Scott 09-16

---

Any online active object recognition system must have

five distinct, fundamental capabilities:

    1. Using the current camera parameters, acquire an

       image, determine the most likely recognition

       hypotheses and give them each a score. This is the

       recognition module.

    2. Combine scores from all views of the object thus

       far into an aggregate score for each of the most

       likely hypotheses. This is the data fusion module.

    3. Decide if the decision threshold has been reached,

       and if so, declare a recognition. This is the

decision module.

    4. If no decision can be reached based on current

       view sequence, select the next camera parameters.

       This is the view planning module.

5. Servo the camera platform to the next desired

       position in parameter space. This is the gaze

       control module.

CSE668 Sp2011 Peter Scott 09-17

---

So for active OR we observe-fuse-decide-plan-act. Note

that some of these modules are logically independent,

such as the decision and gaze control modules, so we

can "mix and match" their designs. Others, like the

fusion module and the planning module, are logically

connected and should be selected together.

Before discussing Borotschnig's implementation of the

observe-fuse-decide-plan-act paradigm for active vision,

we should note that there are other ways of categorizing

the tasks involved in formulating an active task-oriented

response to a set of perceptions. Among the most frequently

cited is the OODA (Observe-Orient-Decide-Act) loop which has

been the basis of much of the so-called C^₃I automation

applications of the US military (command - control -

communications - intelligence).

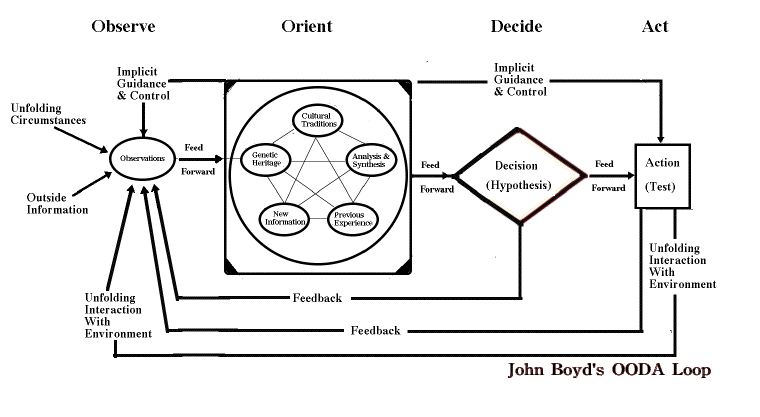
                                                                                                                            ---  Courtesy www.airpower.maxwell.af.mil

CSE668 Sp2011 Peter Scott 09-18

---

Borotschnig's Appearance-based active OR

A good example of a complete active OR system is that

designed by a group form the Technical University at Graz,

Austria led by Hermann Borotschnig (see course web page for

complete citation).

1. The recognition module

They base their recognition logic on Principal Component

Analysis (PCA). PCA is a quite general procedure, not just

limited to image processing, for projecting a numerical

vector down into a lower-dimensional subspace while keeping

the most important properties of the vector. It is called

a "subspace" method. What defines PCA is that it is the

most accurate subspace method in the least-squares sense.

CSE668 Sp2011 Peter Scott 09-19

---

PCA

Given a set of n-dimensional vectors X, the goal of PCA is

to specify an ordered set of n orthonormal vectors E={ej}

in Rⁿ such that each xi in X can be expressed as a linear

combination of the ej's

    x_i = a_i1e₁+a_i2e₂+...+a_ime_m...+a_ine_n

and so that for all m<n, if xi is approximated by the just

its first m terms,

    x_i' = a_i1e₁+a_i2e₂+...+a_ime_m

the total mean-square error over the entire dataset

    sum_i (x_i-x_i')²

is minimum over all choices of the ordered set E.

The orthonomal basis E for Rⁿ is called the set of

principal components of the set X.

CSE668 Sp2011 Peter Scott 09-20

---

Thus e₁ is the basis for the best one-dimensional space

to project X down into in the ms sense. (e₁,e₂) is the

best 2-dimensional space, and in general (e₁,...,e_m) is

the best m<n dimensional space to project X into in the

ms sense.

The principal components answer the question: if you

had to approximate each x as a linear combination of

just m fixed vectors, which m would you choose? In other

words, what is the best way to approximate a given set of

vectors from Rn by projection into a lower-dimensional

space R^m.

CSE668 Sp2011 Peter Scott 09-21

---

Eg: Three vectors X={x₁,x₂,x₃} in 2 dimensions. e₁ is

    the first principal component, e₂ the second.

    There is no other vector that is better than e1

    in the sense of minimizing the total error

    mserror=1/3(error₁^Terror₁+error₂^Terror₂+error₃^Terror₃)

CSE668 Sp2011 Peter Scott 09-22

---

Applying PCA to the active OR context

First consider the offline (training) steps. For a selected

set of objects {o_i} to be recognized, and of viewpoints

{p_j}, we acquire images. Each of these images is then

normalized to the same size and average brightness.

Now lets rewrite each image as a vector, say using raster

ordering, to create image vectors x_ij of dim(N). So for

instance, for a 512x512 image, N=512*512=262144. There will

be Nx = (number of objects)x(number of viewpoints) such

image vectors x_ij.

CSE668 Sp2011 Peter Scott 09-23

---

Let xbar be the average image vector

        xbar=(1/N_x)(sum_ij x_ij )

Define the vector X by concatenating the vectors (x_ij-xbar)

as column vectors. Then the covariance matrix of the image

set {x_ij} is defined as

        Q = XX^T

Note that dim(Q)=NxN, so for instance in a 512x512 image

case with N=262144, Q is a 262144x262144 matrix with

2¹⁸x2¹⁸=2³⁶ or about 68 giga-elements.

The principal components of the image set {x_ij} are then

the eigenvectors of Q, ordered in descending order of the

magnitudes of their eigenvalues.

CSE668 Sp2011 Peter Scott 09-24

---

Since Q is symmetric and positive semi-definite, its

eigenvectors will be orthogonal and can be considered

normalized. Also, its eigenvalues will be non-negative.

The fractional mean square error in projecting {xij} into

the subspace spanned by the first m principal components is

    FMSE = sum_i>m(λ_i²⁾/ sum_j<=N(λ_j² )

where {λ₁, λ₂,..., λ_N} are the eigenvalues in

descending order (largest first).

CSE668 Sp2011 Peter Scott 09-25

---

Eg: Consider an N=4 pixel image set with eigenvalues

λ₁=7, λ₂=3, λ₃=2, λ₄=1. Then if we project

the images into the 1-D subspace spanned by just its

first principal component (first eigenvector), the

fractional square error will be

    FMSE = (3^2+2^2+1^2)/(7^2+3^2+2^2+1^2) =

          = 14/63 = 0.222

So the fractional average error will be sqrt(FMSE)

or .471. Thus projecting from 4-D to 1-D we will

lose about half the original image information.

Note: the projection of a vector x into the 1-D subspace

spanned by the eigenvector e₁ is the best approximation of x

as a*e₁, where the coefficient vector a minimizes the error

||x-a*e₁||.

CSE668 Sp2011 Peter Scott 09-25a

---

If we project into a 2-D subspace of the first two

eigenvectors,

    FMSE = (2^2+1^2)/(7^2+3^2+2^2+1^2) = 0.0794

and the fractional average error will be sqrt(.0794)

or .28. So we will have lost about a quarter of the

image information in projecting into 2-D.

The projection of a vector x into the 2-D subspace spanned

by the eigenvectors e₁ and e₂ is the best approximation of x

as a₁*e₁+a₂*e₂, where the coefficients a₁ and a₂

minimize the error ||x-(a₁*e₁+a₂*e₂)||.

CSE668 Sp2011 Peter Scott 09-26

---

Based on the eignevalues (λ's) we compute offline, we can

determine the FMSE using only the first k principal components,

for k=1,2,.. until the FMSE is sufficiently low for our error

tolerance. We select this k and this becomes the dimension

of the principal component subspace we will use for

approximating image vectors, the subspace spanned by

the first k eigenvectors {e₁,...,e_k}, also called the

principal components of the training data set.

So given any image vector x, dim(x)=N, we approximate

x by g, dim(g)=k, where

           g = sum_i(g_i*e_i)

where the gi are the scalar weights of the various

eigenvectors in approximating x in the reduced space

of dimension k<<N, which are given by the inner products

of the pattern x with the eigenvectors:

          g_i = x^Te_i

CSE668 Sp2011 Peter Scott 09-27

---

Now back to Borotshnig's active object recognition

scheme. Besides the projection of a given vector into a

selected k-dimensional principal component subspace,

the other thing we must approximate offline is the

probability density function of g, for each object o_i

and pose p_j, P(g|o_i,p_j). This is done by taking a set

of sample images with fixed (o_i,p_j) but varying the

lighting conditions, and fitting the resulting set of

g-values by a Gaussian distribution.

CSE668 Sp2011 Peter Scott 09-28

---

P(g|o_i,p_j) can be used through Bayes' Law to determine

posterior probabilities of object-pose hypotheses

    P(o_i,p_j|g) = P(g|o_i,p_j)P(o_i,p_j)/P(g)

and the posterior object probabilities

    P(o_i|g) = sum_jP(oi,pj|g)

Thus, the most likely hypotheses (o_i,p_j) and their

scores P(o_i,p_j|g) can be determined by the recognition

module online by projecting x down to g and using the

offline probability database to get the hypothesis

probabilities. Marginalizing (summing the joint probabilities)

over the poses yields the posterior probabilities of each

object class given the image data g.

CSE668 Sp2011 Peter Scott 09-29

---

2. Data Fusion Module:

Using this Bayesian approach, data fusion becomes

straightforward. Given a set of n image vectors

{x1..xn} which project to their PCs {g₁...g_n},

  P(o_i|g₁..g_n)=P(g₁..g_n|o_i)P(o_i)/P(g₁..g_n)

Lets determine this overall probability recursively

assuming class-conditional independence

    = P(g₁..g_n-1|o_i)P(g_n|o_i)P(o_i)/P(g₁..g_n)

    = P(o_i|g₁..g_n-1)P(o_i|g_n)P(o_i)/D

where D = P(g₁..g_n)/(P(g₁..g_n-1)P(g_n))

CSE668 Sp2011 Peter Scott 09-30

---

3. Decision module: decide o_i at time n if

        i=arg max P(o_i|g₁..g_n)

and     P(o_i|g₁..g_n) > T

where T is a preselected threshold. So for

instance if you require P(error)<5% you would

set T=0.95+V, where V>0 is chosen to correct for

sampling error in estimating the various probabilities.

CSE668 Sp2011 Peter Scott 09-31

---

4. Where do we look next? Define the uncertainty in

the object recognition task at time n as the entropy

    H(O|g₁..g_n) = -sum_i(P(o_i|g₁..g_n)P(g₁..g_n))

of the prob density function of the random variable

O where O=o_i if and only if the object class is i.

Now for each candidate change in the camera parameters

we can determine the expected reduction in the entropy.

This expected reduction depends on the {P(o_i,p_j|g₁..g_n)},

the current hypothesis probabilities. For instance, if

there are two very probable hypotheses and there is a

way to change camera parameters to eliminate one or the

other, that next-look with have a low expected entropy.

Their approach to view planning is to select the next

view (camera parameters) which minimizes the expected

entropy. See (9)-(11) in the paper for details.

CSE668 Sp2011 Peter Scott 09-32

---

5. Gaze control module: a control strategy to implement

the physical motion, ie. the view planning outcome. Not

of interest here.

CSE668 Sp2011 Peter Scott 09-33

---

Strengths and Limitations of the Borotschnig approach

Strengths

A major strength is that it is a complete end-to-end

active vision OR system based on well understood

mathematical tools (PCA, Bayesian scoring, entropy).

Another strength is that it is domain-independent,

and the database can be incrementally updated.

In addition, Borotshnig's procedure does not require

segmentation preprocessing, so the matching of test

data is fast.

CSE668 Sp2011 Peter Scott 09-34

---

Limitations

A major problem with applying PCA to OR is that

it is highly sensitive to object location in the object

plane. Shifting the image radically changes the PCs.

Eg:

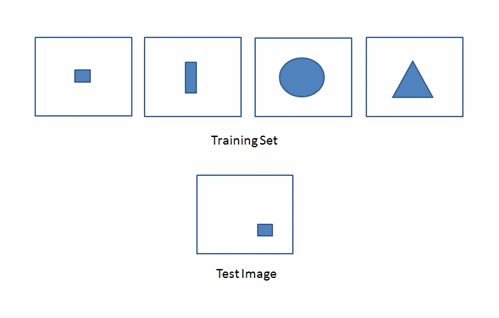
Principal component analysis guarantees that the images

in the training set, and images very similar to them,

can be recognized using just a few principal components.

But if an object is shifted in an image, like the test

image above, its ms error compared to the corresponding

image in the training set will be large, and the principal

components will not be effective at capturing the test image,

    thus OR based on them will likely fail. Position counts!

CSE668 Sp2011 Peter Scott 09-35

---

    In general, PCA is not invariant under affine transformations,

of which pure translation is the most difficult to avoid. But

rotation and scaling also must either be forbidden by tightly

controlling the imaging environment, or otherwise be somehow

compensated.

PCA is not invariant under lighting changes either. So large

scale lighting changes will confound a PCA OR scheme.

Finally, it should be noted that PCA is a global rather than

local matching procedure. This leads to problems with

occlusion and clutter as Nelson discusses in the context

of local vs. global keys.

CSE668 Sp2011 Peter Scott 09-36

---

These difficulties can each be addressed, but together

probably limit the application of the method to highly

constrained domains, like automated part inspection or

"toy" problem domains.

A good approach to (relatively) unconstrained, natural-vision

active OR has yet to be discovered. This is a great challenge

for the next generation of researchers in the computer vision

field!

CSE668 Sp2011 Peter Scott 09-37

---