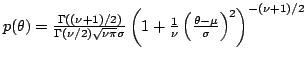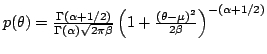|
Distribution |
Notation |
Parameters |
Density function |
Moments, entropy, KL-divergence, etc. |
Notes |
|
|---|
| Uniform |
|
|
|
|
|
|
| Exponential |
|
|
|
|
|
|
| Laplace |
|
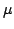 mean mean |
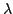 decay scale decay scale |
|
|
|
|
|
| |
|
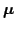 mean vector mean vector |
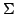 covariance covariance |
|
|
|
|
|
| |
|
|
|
|
|
|
| Gamma |
|
shape 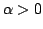 |
inv. scale 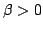 |
|
|
|
|
conj. Gaussian precision |
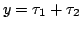 where where |
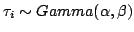 then... then...
|
|
|
| Inverse gamma |
|
|
|
|
|
|
|
Wishart |
|
deg. of freedom 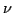 |
precision matrix 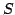 |
|
|
|
|
|
| Inverse-Wishart |
|
deg. of freedom 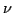 |
covariance matrix 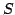 |
|
|
| entropy |
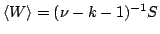 |
|
| conj. Gaussian covariance |
If
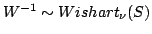 , then , then |
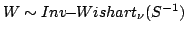 |
|
|
|
| Student-t (1) |
|
deg. of freedom 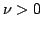 |
mean 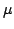 ; scale ; scale 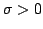 |
|
|
|
|
|
| Student-t (2) |
|
|
|
![$ H_\theta = \left[ \psi(\alpha+\frac{1}{2}) - \psi(\alpha) \right] (\alpha+\frac{1}{2}) + \ln \sqrt{2\beta} B(\frac{1}{2},\alpha)$](img76.png) |
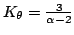 (relative to Gaussian) (relative to Gaussian) |
equiv.
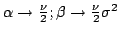 |
|
|
|
| |
|
deg. of freedom 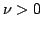 |
mean
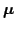 ; ;
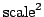 matrix matrix 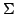 |
|
|
|
|
|
| Beta |
|
| prior sample sizes |
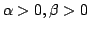 |
|
|
|
|
|
| Dirichlet |
|
| prior sample sizes |
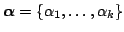 |
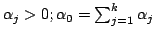 |
|
|
|
|
|
| |
|
number 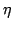 and value and value
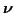 |
| of pseudo-observations |
|
|
|
|
|
|
|
|
|
|
|
|