I design machine learning algorithms that try to solve some of today's most challenging problems in computer science and statistics.

I adapt ideas from physics and the statistical sciences, and use them in algorithms that can be applied to areas such as: bioinformatics, artificial intelligence, pattern recognition, document information retrieval, and human-computer interaction.

Click on the following topics to see research descriptions and some papers:-

Nonparametric Bayes - powerful nonparametric text/document modelling
Variational Bayesian Methods - approximate Bayesian learning and inference
Bioinformatics - microarray analysis using variational Bayes
Embedded Hidden Markov Models - a novel tool for time series inference
Probabilistic Sensor Fusion - combining modalities using Bayesian graphical models
Collaborators - people I have worked with

Variational Bayesian methods

Variational methods are a powerful tool from statistical physics that I have used to approximate Bayesian learning. Bayesian learning relies on a key quantity, the marginal likelihood, which results from averaging over the parameters of the model. In nearly every interesting scenario these averages are analytically intractable, and we are forced to work with approximations. Variational Bayesian methods offer a fast and efficient alternative to sampling techniques, and moreover offer an approximation in the form of a bound on the marginal likelihood.

My thesis presents a tutorial of variational methods, discusses and extends the theory behind the VB approximation, and applies it to several well-used algorithms in CS and statistics. These include models such as Mixtures of Factor Analysers, State-Space Models (Linear-Gaussian Dynamical Systems), and Hidden Markov Models.

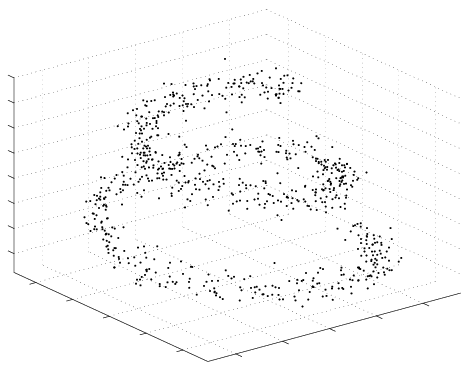
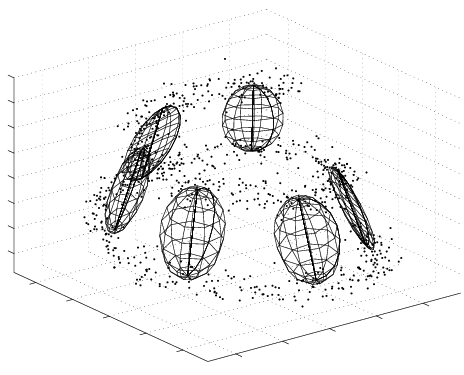
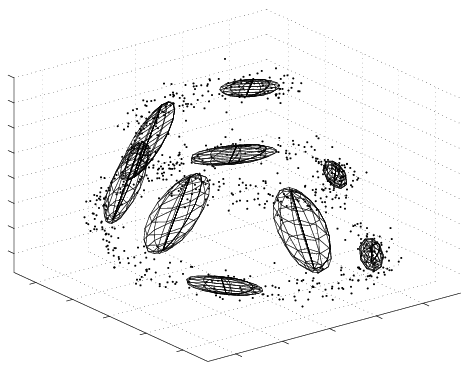
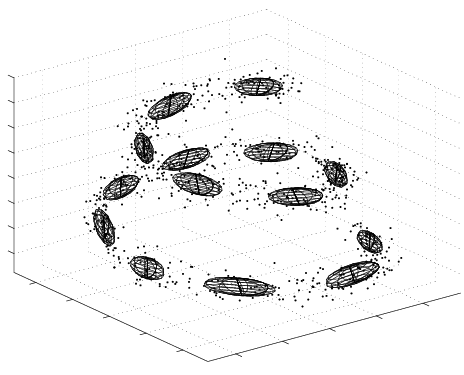
Example of a Variational Bayesian Mixture of Factor Analysers (VBMFA) discovering a non-linear 1-d manifold embedded in a 3-d space (the spiral). Iterations run from left (the data) to right (the final solution).

My work concentrates on a particular class of models called conjugate-exponential, which encompass the models described above, as well as a host of other models; I delve into these types of models and examine the variational Bayesian updates in detail. A number of key results are presented in the thesis. These include a general importance sampling methods for estimating the tightness of the VB lower bound. Also we show that the well-used Cheeseman-Stutz approximation to the marginal likelihood is not only itself a lower bound (similar to the VB lower bound), but also that there exists a straightforward construction which shows that the VB lower bound is universally tighter.

In the final chapter I show that VB outperforms standard model selection criteria, such as BIC and the Cheeseman-Stutz criterion, and comprehensively compare the VB performance to a gold-standard Annealed Importance Sampling (AIS) estimate. For a given accuracy we find that the VB algorithm needs less than 1% of the computational time that is required of the AIS sampling estimate.