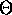 to mean `order exactly', O to mean `order at most',
and
to mean `order exactly', O to mean `order at most',
and 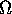 to mean `order at least'.
to mean `order at least'.
We use 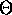 to mean `order exactly', O to mean `order at most',
and
to mean `order exactly', O to mean `order at most',
and 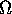 to mean `order at least'.
to mean `order at least'.
Definition of 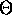 :
Given nonnegative functions f and g defined on the
positive integers, we write
:
Given nonnegative functions f and g defined on the
positive integers, we write 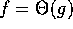 if and only if there are
positive constants
if and only if there are
positive constants 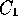 ,
, 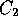 , and a positive integer N
such that
, and a positive integer N
such that
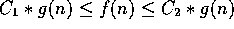 ,
whenever n>N.
,
whenever n>N.
Definition of O:
Given nonnegative functions f and g defined on the positive integers,
we write f=O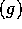 if and only if there is a positive constant C and an
integer N such that
if and only if there is a positive constant C and an
integer N such that
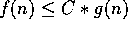 , for all n>N.
, for all n>N.
Definition of  :
Given nonnegative functions f and g defined on the positive integers,
we write
:
Given nonnegative functions f and g defined on the positive integers,
we write  if and only if there is a positive constant C
and an integer N such that
if and only if there is a positive constant C
and an integer N such that
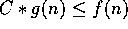 , for all n>N.
, for all n>N.
When using order notation, one wants to use the simplest function
possible within the 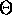 , O, or
, O, or 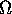 .
The idea is to use the notation to reduce complicated functions to
simpler ones whose behavior is easier to understand.
.
The idea is to use the notation to reduce complicated functions to
simpler ones whose behavior is easier to understand.
Proposition 1:
Suppose f and g are positive functions defined
on the positive integers, and that
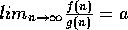 ,
for some nonzero a.
Then
,
for some nonzero a.
Then 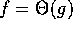 .
.
Proof: 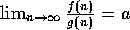 means that for any c>0 there
is an integer N such that
means that for any c>0 there
is an integer N such that 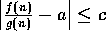 ,
for all
,
for all 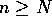 .
If we chose
.
If we chose 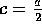 then there is an N such that
then there is an N such that
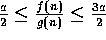 for all
for all 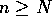 .
So,
.
So, 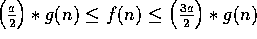 ,
for all
,
for all 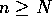 .
. 
Proposition 1 is useful because there are many techniques, such as L'Hopital's rule, for evaluating limits. However, there are some instances where Proposition 1 cannot be used.
For example, 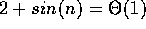 , even though
, even though
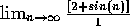 is undefined.
is undefined.
Examples of  :
If
:
If 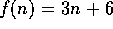 and
and 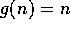 , then
, then
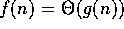 , or
, or  , or
, or 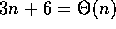 ,
as can be seen by using
,
as can be seen by using 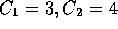 , and N=5.
, and N=5.
Notice that if 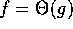 then
then 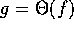 , since if there
are positive constants
, since if there
are positive constants 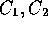 , and N such that
, and N such that
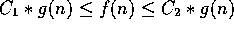 for all n>N, then
for all n>N, then
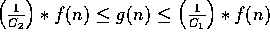 ,
for all n>N.
,
for all n>N.
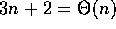 .
.
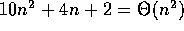 .
.
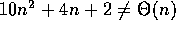 .
.
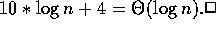
Useful Properties of 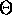 :
:
1. If 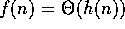 and
and 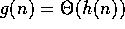 , then
, then
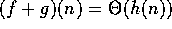 .
.
2. If 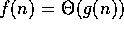 and
and 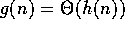 , then
, then
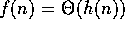 .
.
3. 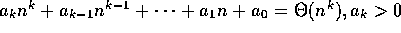 .
.
4. 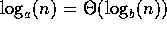 for any a,b>1.
for any a,b>1.
5. 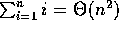
6. 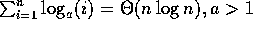 .
.
7. 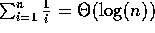 .
.
8. 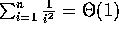 .
.
9. If 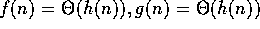 ,
and
,
and 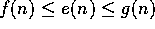 ,
then
,
then 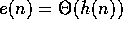 .
.
O and 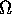 Notation
Notation
It is not always possible to determine the behavior of an algorithm
using 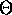 -notation.
For example, given a problem with n inputs, we may have
an algorithm to solve the problem which takes
-notation.
For example, given a problem with n inputs, we may have
an algorithm to solve the problem which takes 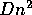 time when n is even
and Cn time when n is odd.
Or, we may only be able to prove that an algorithm
never uses more than
time when n is even
and Cn time when n is odd.
Or, we may only be able to prove that an algorithm
never uses more than 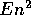 time and never less than
Fn time.
In either circumstance we can claim neither
time and never less than
Fn time.
In either circumstance we can claim neither 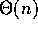 nor
nor
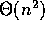 to be the order of the time usage of the algorithm.
O and
to be the order of the time usage of the algorithm.
O and 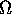 notation will allow us to give at least partial information.
notation will allow us to give at least partial information.
Proposition 2: Suppose f and g are positive functions
defined on the positive integers, and that
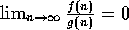 ,
then f=O
,
then f=O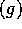 .
. 
Examples of O:
3 n + 2 = O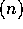 , since
, since 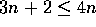 , for all
, for all 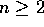 .
100 n + 6 = O
.
100 n + 6 = O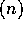 , since
, since 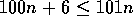 , for all
, for all 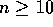 .
.
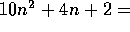 O
O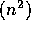 , since
, since 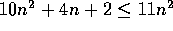 ,
for all
,
for all 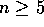 .
.
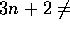 O
O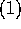 , since 3 n + 2 is not less than or equal to
c for any constant c and all
, since 3 n + 2 is not less than or equal to
c for any constant c and all 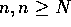 .
.
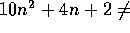 O
O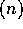 .
.
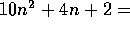 O
O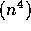 .
. 
Proposition 3: Suppose f and g are positive functions
defined on the positive integers, and that
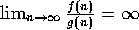 ,
then
,
then 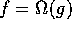 .
. 
Examples of 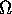 :
:
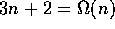 , since
, since 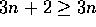 for all
for all 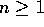 .
.
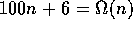 , since
, since 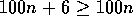 for all
for all 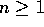 .
.
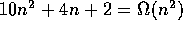 since
since
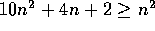 for all
for all 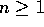 .
.
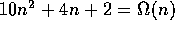 .
.
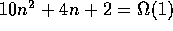 .
. 
Useful Properties of O and 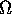 :
:
1. 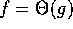 if and only if f=O
if and only if f=O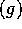 and
and 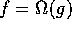 .
.
2. If f=O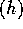 and g=O
and g=O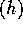 then f+g=O
then f+g=O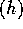 .
.
3. If 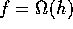 and
and 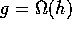 then
then 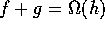 .
.
4. If f=O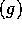 and g=O
and g=O then f=O
then f=O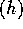 .
.
5. If 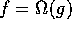 and
and 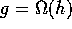 then
then 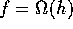 .
.
6. Suppose 0<a<b. Then 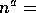 O
O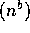 and
and 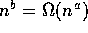 .
.
7. Suppose 0<a and 1<b, then 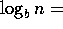 O
O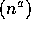 and
and
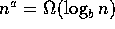 .
.
8. Suppose 1<c and 0<a, then 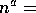 O
O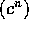 and
and 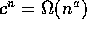 .
.