RTS: Clock-driven Scheduling

September 21by Bina

Announcements: Codecon for the course is set up and ready to go. NOTE: We started this lecture on 16th Sept., we will finish it with a realtime scheduling for the problem on the right.

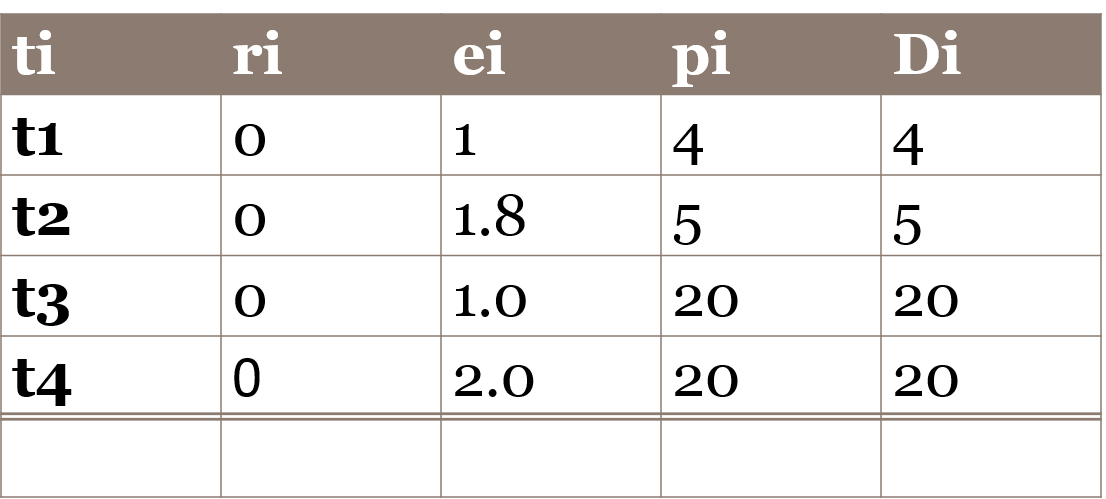
Consider a set of N period tasks. Your goal is to design a cyclic executive for the N tasks. A periodic task is denoted by {tai, ei ,pi, Di} where the attributes are arrival time, execution time, period and relative deadline for task i For example {0, 5, 12, 7} means


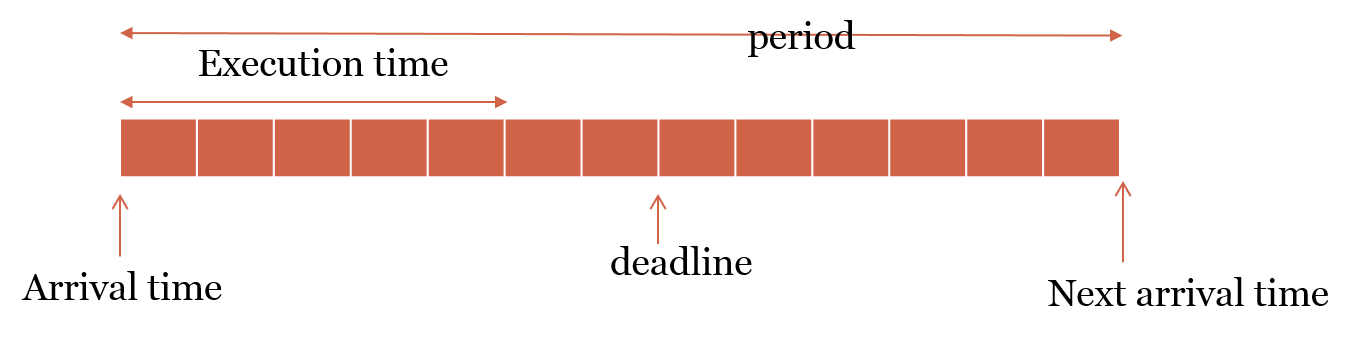
How will the timing diagram be for {1, 5, 12, 7} and for {0, 5,12, 12}? Lets discuss.

Problem Statement: n periodic tasks with {tai, ei ,pi, Di} with i = 1..n need to be scheduled. Since the four parameters known ahead the scheduling is static and a cyclic executive can be designed to schedule (& execute) the tasks so that they meet their respective deadlines.

Rules for designing a cyclic executive

1. Utilization U = ∑ (ei/pi) if utilization U>1, the tasks cannot be scheduled in the same processor.
2. If U is okay, Hyperperiod H is lcm (pi) + these constraints
   • Frame f ≥ max(ei)
   • Frame f should evenly divide H.
   • There should be at least 1 frame between release time of a task and its deadline: 2f – gcd(pi,f) ≤ Di
   Very often Di and Pi are same for periodic task. We will assume this simplification.

Example: Given the task set on the sidebar design the cyclic executive schedule or clock driven static schedule.

Hmmm.. how do we implement this in code?
Using table-driven (or data-driven) code

Rate monotonic scheduling (RMS)

Periodic tasks are prioritized by the frequency of repetition (high priority to tasks with shorter periods)
Preemptive scheduling is commonly used.
Schedulability according to RMS Σ(Ci/Ti) <= n(pow(2,1/n)-1)
Cyclic executives (pre-scheduled)