Proofs by Induction
We review some examples of proof by induction. While doing this, we will also go through examples of how to write proof ideas and details as well as algorithm ideas and details (which you will need to write in your homework solutions).
-
Short for Left Hand Side.
-
You guessed it: short for Right Hand Side.
-
Don't worry, we'll see soon why this problem can make a lot of sense.
-
Convince yourself that such a number always exists!
-
Fun exercise: how many distinct trees are there for a given value of n?
-
Note that even for fixed values of
mandn, there are infinitely many possibilities for the inputsAandB. -
Prove this!
A Simple Example
We begin with a simple example. Consider the following code snippet (some variant of which you must have seen and used many times):
for( i=0; i< n; i++)
for(j=0; j<= i; j++)
print("Blah");
We then ask the burning question that is on everyone's mind:
Question
How many times (in terms of n) does the program snippet above print Blah?
It is not too hard to see that for each value of $i=0,1,\dots,n-1$, the index $j$ goes from $j=0,\dots,i$. That is, the index $j$ takes on exactly $i+1$ distinct values. Further for each such distinct pair $(i,j)$, the code above prints Blah exactly once. Thus, the total number of times Blah is printed is exactly
\[\sum_{i=0}^{n-1} (i+1) = \sum_{i=1}^n i = 1 +2 +\cdots +n.\]
While the sum $1+2+\cdots n$ is a valid answer it is not that useful especially when we would like to do some asymptotic analysis. Further, for purely aesthetic reasons it would be nice to have a closed form expression. And indeed there is one:
Lemma 1
For every integer $n\ge 1$, we have \[\sum_{i=1}^n i = \frac{n(n+1)}{2}.\]
Proof Idea
We will prove the lemma using induction on $n$. The inductive steps depends on some simple algebraic manipulations that allow us to prove the identity: \[\frac{m(m+1)}{2}+(m+1)=\frac{(m+1)(m+2)}{2}.\]
Proof Details
Base Case We have $n=1$. In this case the LHS1 is $\sum_{i=1}^1 i =1$ while the RHS2 is $\frac{1(1+1)}{2}=1$ and hence the identity in the Lemma 1 is correct for the base case.
Inductive Hypothesis Assume that the identity holds for $n=m$ for some $m\ge 1$.
Inductive Step Now consider the case when $n=m+1$. Now we have the LHS of the identity is \[\sum_{i=1}^{m+1} i = \sum_{i=1}^m i + (m+1),\] where the equality follows by separating out the last term in the sum. Now by inductive hypothesis we have that \[\sum_{i=1}^m i = \frac{m(m+1)}{2}.\] Using the two identities above, we have that \[\sum_{i=1}^{m+1} i = \frac{m(m+1)}{2}+(m+1) = (m+1)\cdot \left(\frac{m}{2}+1\right) = \frac{(m+1)(m+2)}{2},\] where the last two equalities follows from simple algebraic manipulation. Finally, we note that $\frac{(m+1)(m+2)}{2}$ is the RHS of the identity for $n=m+1$, which completes the inductive step and hence the proof of the lemma.
Below is a Khan Academy video for the same proof:
Two Digressions
Lemma 1 was an excuse to show you a proof by induction. However, I have two other reasons why I used this example as opposed to many others I could have started with: one historical and one algorithmic.The Historical Digression
I will start the discussion about the history behind Lemma 1 with an alternate proof (idea) for Lemma 1:
Proof Idea
For simplicity, let us assume that $n$ is even. Then group the numbers in the sum $1+2+\cdots n$ in pairs from "outside in" \[ (1,n), (2,n-1),\cdots, (i,n-i+1),\cdots \left(\frac{n}{2},\frac{n}{2}+1\right).\] Now note that there are $\frac{n}{2}$ pairs; the numbers in each pair sum up to $i+n-i+1=n+1$ and finally, each number in the sum$\sum_{i=1}^n i$ appear in exactly one such pair. The proof follows by noting that the sum is $n/2$ times the sum of the numbers of each pair, which is exactly $\frac{n(n+1)}{2}$.
If you need practice on writing proof details, write the proof details for the proof idea above as an exercise. If not or if you want to see the proof details, click here.
Proof Details
First consider the case when $n$ is even. Then consider the following identities: \[ \sum_{i=1}^{n} i = \sum_{i=1}{\frac{n}{2}} (i + n+1-i) = \sum_{i=1}{\frac{n}{2}} (n+1) =\frac{n(n+1)}{2},\] where the first equality follow by pairing every $i\in [n/2]$ with $n+1-i$.
Now consider the case where $n$ is odd. Further, consider the following identities: \[\sum_{i=1}^n i =\sum_{i=1}^{\frac{n-1}{2}} i + \frac{n+1}{2} +\sum_{i=\frac{n+3}{2}}^n i= \frac{n+1}{2}+\sum_{i=1}^{\frac{n-1}{2}} \left( i +n+1-i\right) = \frac{n+1}{2}+\frac{n-1}{2}\cdot (n+1) = \frac{n(n+1)}{2}.\]
Here is the Khan academy video of the same proof as above (stated in a slightly slicker way)
It is claimed that Gauss discovered this proof when he was seven(!) years old. The story goes that Gauss' math teacher wanted to keep his students busy and asked them to calculate $1+2+\cdots+100$, thinking that they would manually add the $100$ numbers. Apparently, Gauss figured out the quick proof and the identity above and promptly came up with the correct answer. (See this article for a more detailed account of this incident.)
The Algorithmic Digression
We begin with the following problem3:Find the missing number
Given $n-1$ numbers $a_0,\dots,a_{n-2}$ such that $a_i\in [n]$ for every $i$ and all the numbers are distinct. Output the missing number: i.e. the number $j\in [n]$ such that $a_i\neq j$ for every $0\le i \lt n-1$.4
Pft, you say. What is the big deal with the problem above (and what does Lemma 1 have to do with this)? You can easily solve the problem as follows.
Algorithm Idea
Maintain a Boolean array with $n$ entries, one for each element in $[n]$. When reading $a_i$, set the corresponding entry to be true. At the end output the entry that is set to false.
Algorithm Details
//Input is A[0], ..., A[n-2] check = new bool[n]; //We will assume that the index starts with 1 for(j=1; j<= n ;j++) check[j]=false; for (i=0; i< n-1;i++) check[A[i]]=true; for(j=1; j<= n; j++) if(!check[j]) return j;
With the current definition of the problem, the solution above is perfectly fine. However, say you want to solve this problem on a router that has to solve the problem for say $n=10^6$ (think a large file is being sent that is divided into $10^6$ packet and one of them is missing and the router wants to find out which one). As you might imagine, router have to work extremely fast and be extremely light-weight. In particular, we want to find out the missing number but with the following additional constraints:
- The algorithm/router can look at each number/packet only one and in the order it receives them, i.e. make one pass over the data.
- The algorithm can only use $O(\log{n})$ temporary space (this is enough to store the IDs of a few packets by the router but no more).
- The algorithm/router needs to output the missing $j$ in $O(\log{n})$ time once it was received all the numbers/packets.
Unfortunately the algorithm above does not meet the last two criteria (though it does satisfy the first one). Indeed check has n entries (and hence the algorithm uses $\Omega(n)$ space) while lines 11-13 can take $\Omega(n)$ time in the worst-case to output the missing number. It turns out that one can use Lemma 1 to design a streaming algorithm to solve the missing number problem:
Exercise
Present an algorithm that solves the missing number problem with one pass over the data, uses $O(\log{n})$ temporary space and reports the missing number in time $O(\log{n})$ after it has made its pass over the data.
Hint: Use Lemma 1.
If you are curious about streaming algorithms, this survey by Muthu Muthukrishnan is perhaps the best place to start. (As a bonus it also solves the exercise above.)
Types of Inductive Proofs
It turns out that the inductive proof of Lemma 1 we saw above is what is known as mathematical induction . The main idea here is that whatever statement you are trying to prove holds for every natural number $n$. For Lemma 1, the statement is the identity that we need to prove. In other words, for each value of $n$ there is only one statement that we need to prove. In other words, the proof is very "linear". To illustrate what we mean consider the animation below, which repeats the inductive step till $n=19$. (Click the "Next" button to perform one inductive step. $S(n)$ denotes the sum $\sum_{i=1}^n i$ and the sum $S(n-1)$, while computing $S(n)$, is denoted in red to highlights where the induction hypothesis is used.)
Before we move on to the next kind of induction proof, here is a fun exercise for mathematical induction:
Exercise
Prove that for any integer $n\gt 1$, any sentence with $n$ occurrences of the word "buffalo" (and no other words) is a grammatically correct sentence.
Hint: You will need to know your grammar pretty well to able to do this!
Sentences involving repetition of "buffalo" are attributed to our very own Bill Rapaport : see his Buffalo buffalo buffalo buffalo buffalo page. If you need a solution sketch for the exercise above, this page has an outline.
Structural Induction
In CSE 331 we will rarely do mathematical induction (as outlined above). Rather we will mostly deal with its generalization called structural induction . In structural induction we will again a single natural number parameter say $n$ but now for each parameter we will have to deal with more than one object. (Recall that for mathematical induction we only had one object for every value of $n$.) For example we might want to prove some property of tree by induction. In this case (typically!) with the parameter $n$ the proof will associate all trees on $n$ vertices: note that there are multiple such trees for $n\gt 2$.5An Example With Trees
We will consider an inductive proof of a statement involving rooted binary trees. If you do not remember it, recall the definition of a rooted binary tree: we start with root node, which has at most two children and the tree is constructed with each internal node having up to two children. A node that has no child is a leaf.
Recall that the depth of a rooted binary tree is the maximum number of edges it takes to go from the root to any leaf. Consider the following problem:
Exercise
Prove that a rooted binary tree with depth $d$ has at most $2^{d+1}-1$ nodes in it.
Note that in the above there is a parameter/number: the depth $d$. However, when we do induction, we will not just do induction $d$ instead we will do induction on all binary rooted trees of depth $d$.
Proof Idea
We will induct on depth $d$ (or more precisely on binary rooted trees of depth $d$). As usual, the interesting part is proving the inductive step, where we are in a situation as below:
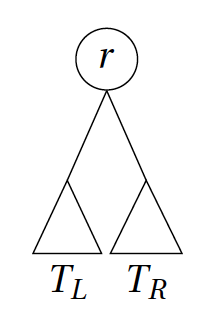
In the above, the root $r$ has up to two children: let the subtree rooted at the left child be called $T_L$ and the subtree rooted at the right child be called $T_R$. The main observation is that if the original tree has depth $d$, then both $T_L$ and $T_R$ have depth at most $d-1$ and thus, we can apply induction on these subtrees.
Proof Details
We will prove the statement by induction on (all rooted binary trees of) depth $d$.
For the base case we have $d=0$, in which case we have a tree with just the root node. In this case we have $1$ nodes which is at most $2^{0+1}-1=1$, as desired.
For the inductive hypothesis, we will assume that any tree with depth $d\le k$ has at most $2^{d+1}-1$ nodes in it. For the inductive step, consider any rooted binary tree $T$ of depth $k+1$. Let $T_L$ denote the subtree rooted at the left child of the root of $T$ and $T_R$ be the subtree rooted at the right child of $T$ (if it exists). Since the depth of $T$ is at least $1$, the root has at least one child. Pick one child and call it the left child and if there is another child, call it the right child. Since the path from the root of $T$ to any leaf in $T_L$ ($T_R$ resp.) has to go through the root of $T_L$ ($T_R$ resp.), which is the left (right resp.) child of the root of $T$, it follows that the depth of both $T_L$ and $T_R$ are at most $k$. By the inductive hypothesis, both of these sub-trees have at most $2^{k+1}-1$ nodes each.
Now the total number of nodes in $T$ is the number of nodes in $T_L$ and $T_R$ plus one (for the root), which is at most \[2\cdot(2^{k+1}-1)+1 = 2\cdot 2^{k+1}-1 = 2^{k+2}-1,\] as desired.
Comparison with structure of proof of Lemma 1
As noted earlier, the structural induction proof above is not "linear" as the mathematical induction proof of Lemma 1. To illustrate this, consider the animation below. It runs the inductive step in the proof above for $d=0,1,2$ (each row corresponds to the same $d$). (Click on "Next" to perform the next inductive step: the animation resets after all the $d=2$ rooted trees have been considered.) The green shaded tree is the current tree of the inductive step, the left sub-tree $T_L$ is denoted by red shaded tree, $T_R$ is blue shaded and if $T_L=T_R$ then it is shaded pink.
Note
In the animation above, the trees were considered in a fixed order. However, in the inductive proof above, all the trees with the same depth can be considered in any order. We fixed the ordering among such tree for illustration purposes.
Analyzing the Merge algorithm
In the previous example of structural induction for each value of the induction parameter $d$, there were multiple objects (i.e. trees of depth $d$) but for each value of $d$, there were only a finite number of objects. However, one can do structural induction when the parameter can have infinitely many objects associated with it. In fact, if you have read the page of asymptotic analysis you have already seen such an example. For completeness, we reproduce that proof here.
We start off with the problem we want to solve:
Merging two sorted lists
Given two lists $A$ and $B$ with $n$ and $m$ integers in sorted order, output the sorted list of $m+n$ elements in $A$ and $B$.
The following algorithm is the well-known Merge algorithm that solves the above problem in time $O(m+n)$.
Algorithm Details
int [] Merge (A, n, B, m)
//Combine two sorted arrays (A of size n and B of size m) into one sorted array of size m+n
{
int C = new int[m+n]; // Initialize the array to be returned
i=j=k=0;
while (i< n and j< m) // Repeat while neither A nor B has been exhausted
{
if(A[i]<B[j])
C[k++] = A[i++];
else
C[k++] = B[j++];
}
while (i< n) //A has not been exhausted
C[k++]=A[i++];
while (j< m) //B has not been exhausted
C[k++]=B[j++];
return C;
}
Recall that we have show that on input A with n elements in sorted order and B with m sorted elements, Merge returns the union of the m+n elements in sorted order (or equivalently the array C returned in line 21 has the elements of A and B in sorted order). We will prove this by induction. As mentioned earlier this will be a (structural) induction proof where for each value of m+n there are infinite possibilities for A and B.
Proof Idea
We will prove the correctness of Merge with a proof by induction on $m+n$. In particular, for the inductive hypothesis we will assume that for every pair of arrays A and B such that the total number of elements in A and B is $m+n$, Merge returns the union of all the elements in A and B in sorted order.6 The proof of the inductive step follows from considering the steps of the Merge sub-routine.
Proof Details
We will induct on $m+n$. In particular, our induction hypothesis is as follows: for every integer $t\ge 2$ the following is true for every pair of positive integers $(m,n)$ such that $m+n=t$. For every possible (non-empty) arrays A (with $n$ elements) and B (with $m$ elements), Merge(A,n,B,m) returns an array C (with $m+n$ elements) that has the elements of A and B in sorted order.
We begin with the base case $t=2$. Since A and B are non-empty this implies that $m=n=1$. We consider the case A[0]<B[0]. In this case in line 11, we will have C[0]=A[0] and in line 19, we will have C[1]=B[0], which is the correct sorted order. Similar arguments handle the case of A[0]>=B[0].
This completes the proof of the base case.
We now present the inductive step. Assume that the induction hypothesis is true for all pairs of arrays (A',B') with size pairs $(n',m')$ such that $m'+n'=t$. Now consider an arbitrary pairs of arrays (A,B) with sizes $(n,m)$ such that $m+n=t+1$. We complete the proof by a case analysis:
A[0]<B[0]. On line 11,Mergewill do the assignmentC[0]=A[0]. (This is the correct assignment sinceA[0]is the smallest element in the union ofAandB.7) If $n=1$, thenMergewill assign all the elements ofBtoC[1,t]in lines 18-19. (Note that in this caseAfollowed byBis the correct sorted order, which is whatCwill contain.) If $n>1$, then letA'=A[1,n-1]andB'=B. Further, the rest of the execution ofMergeis the same as assigningMerge(A',n-1,B',m)toC[1,t]. By the inductive hypothesis (since $m'+n=m+n-1=t$), this implies thatC[1,t]has the elements ofA'andB'in sorted order. SinceA[0]is the smaller than all elements inA'andB', this implies thatCwill have all the elements ofAandBin sorted order.B[0]<=A[0]. The argument is same as in the previous case (where we swap the roles ofAandB).
Since our choice of A and B was arbitrary (subject to the condition $m+n=t+1$), the above argument proves the inductive hypothesis for every array A and B with $m+n=t+1$, which completes the proof.