Networks have been used to describe numerous physical systems in our everyday life, including Internet composed of gigantic networks of webpages, friendship networks obtained from social web sites, and co-author networks drawn from bibliographic data. We regard each node in a network as an object, and there usually exist large amounts of information describing each object, e.g. the hypertext document of each webpage, the profile of each user, and the publications of each researcher. The most important and interesting aspect of these datasets is the presence of links or relationships among objects, which is different from the feature vector data type that we are more familiar with. We refer to the networks having information from both objects and links as information networks. Intuitively, objects connected via the network have many interactions, subsequently share mutual interests, and thus form a variety of communities in the network. For example, in a blogsphere, there could be financial, literature, and technology cliches. Taking communities as contexts, we aim at detecting outliers that have non-conforming patterns compared with other members in the same community.

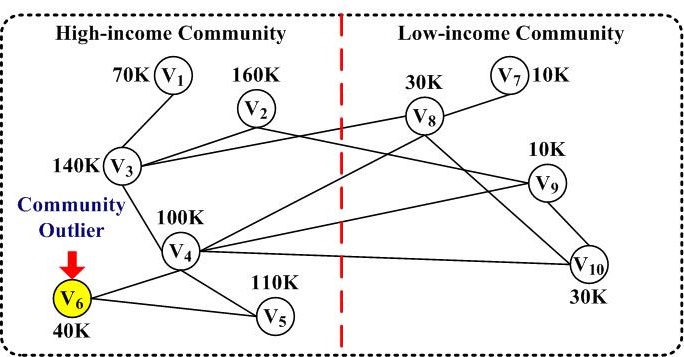
A friend network is shown in the figure above, where each node denotes a person, and a link represents the friend relationship between two persons. Each person's annual salary is shown as a number attached to each node. There obviously exist two communities, high-income (v1,v2,v3,v4,v5) and low-income (v7,v8,v9,v10). Interestingly, v6 is an example of community outliers. It is only linked to the highincome community (70 to 160K), but has a relatively low income (40K). This person could be a rising star in the social network, for example, a young and promising entrepreneur, or someone who may settle down in a rich neighborhood. Another example is a co-author network. Researchers are linked through co-authorship, and texts are extracted from publications for each author in bibliographic databases. A researcher who does independent research on a rare topic is an outlier among people in his research community, for example, a linguistic researcher in the area of data mining. Additionally, an actor cooperation network can be drawn from movie databases where actors are connected if they co-star a movie. Exceptions can be found when an actor's profile deviates much from his co-star communities, such as a comedy actor co-starring with lots of action movie stars.

In detecting community outliers, both the information at each individual object and the one in the network should be taken into account simultaneously. In many applications, no matter the network is dense or sparse, there is ambiguity in community partitions. This is particularly true for very large networks, since information from both nodes and links can be noisy and incomplete. Consolidating information from both sources can compensate missing or incomplete information from one side alone and is likely to yield a better solution.

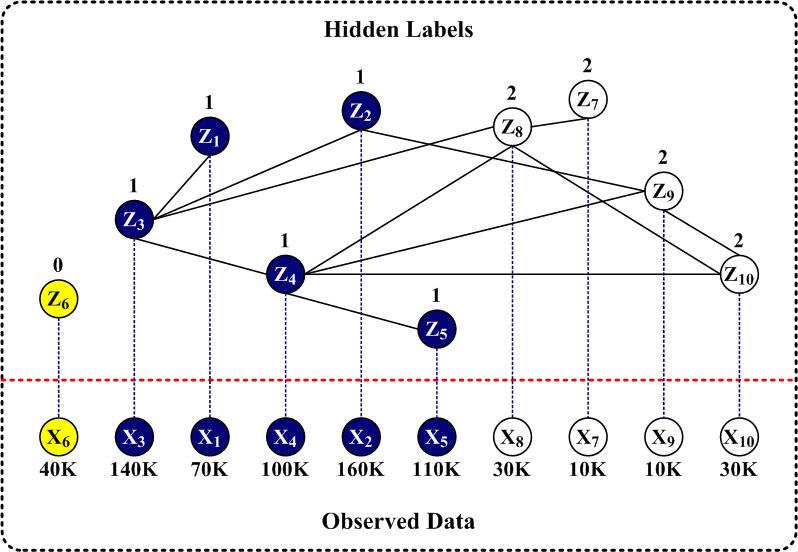
We propose a probabilistic model for community outlier detection in information networks, as illustrated in the figure above. It provides a unified framework for outlier detection and community discovery, integrating information from both the objects and the network. The information collected at each object is formulated as a multivariate data point, generated by a mixture model. We use K components to describe normal community behavior and one component for outliers. Distributions for community components are, but not limited to, either Gaussian (continuous data) or multinomial (text data), whereas the outlier component is drawn from a uniform distribution. The mixture model induces a hidden variable z at each object node, which indicates its community. Then inference on z's becomes the key in detecting community outliers. We regard the network information as a graph describing the dependency relationships among objects. The links from the network (i.e., the graph) are incorporated into our modeling via a hidden Markov random field (HMRF) on the hidden variable z's. We motivate an objective function from the posterior energy of the HMRF model, and find its local minimum by using an Iterated Conditional Modes (ICM) algorithm.