In many applications, we are interested in classifying a set of objects, and the predictive information comes from multiple information sources, each of which either transfers labeled information from relevant domains (supervised classification), or derives grouping constraints from the unlabeled target objects (unsupervised clustering). Multiple hypotheses can be drawn from these information sources, and each of them can help derive the target concept. However, since the individual hypotheses are diversified and heterogeneous, their predictions could be at odds. Meanwhile, the strength of one usually complements the weakness of the other, and thus maximizing the agreement among them can significantly boost the performance. Therefore, we study the problem of consolidating multiple supervised and unsupervised information sources by negotiating their predictions to form a final superior classification solution.

We illustrate how multiple sources provide "complementary" expertise and why their consensus combination produces more accurate results through a real example. Suppose we have seven users and they are using a movie recommendation service. Our goal is to predict each user's favorite movie type as one of {comedy, thriller, action}. Naturally, the first data source for the task involves the movies they have watched, which can be collected from movie review or rental websites. We can infer a user's favorite movie type as the type of the movies he's watched the most often. However, we only have limited access to the list of movies users have seen in practice, then the decision made based on such partial information will contain errors. We can make such predictions based on some other data sources about the users and the movies, such as user taggings and personal information of users. Each of them gives a useful but not perfect classification solution. We can also collect information about how users interact with each other regarding movies from some movie discussion forums or social networks. Based on this data source, we can partition users into several clusters based on their relationships. Users in each cluster are more likely to like the same type of movies. We should try to assign the same movie type to users in one cluster. However, the clustering constraint may not always be correct because sometimes users interact on issues not related to movie types. Again, it is a useful but not perfect data source. We can receive multiple clustering solutions from multiple such sources.

As shown in this table, we have multiple data sources for the task of movie recommendation. Due to distributed computing, privacy preserving or knowledge reuse reasons, we don't have access to raw data of each source, instead, each source just provides labeling or grouping results on the seven users. A labeling solution simply predicts each user's favorite movie type, whereas a clustering solution gives the constraint. Each of the solutions is derived based on partial information. However, these solutions are based on heterogeneous sources and capture different aspects about the label predictions of the target objects. Therefore, they do complement each other. Given all these solutions, our goal is to combine them into a consolidated solution, which leverages different information sources, gives the global picture and thus is more accurate than each base solution derived from a single source.

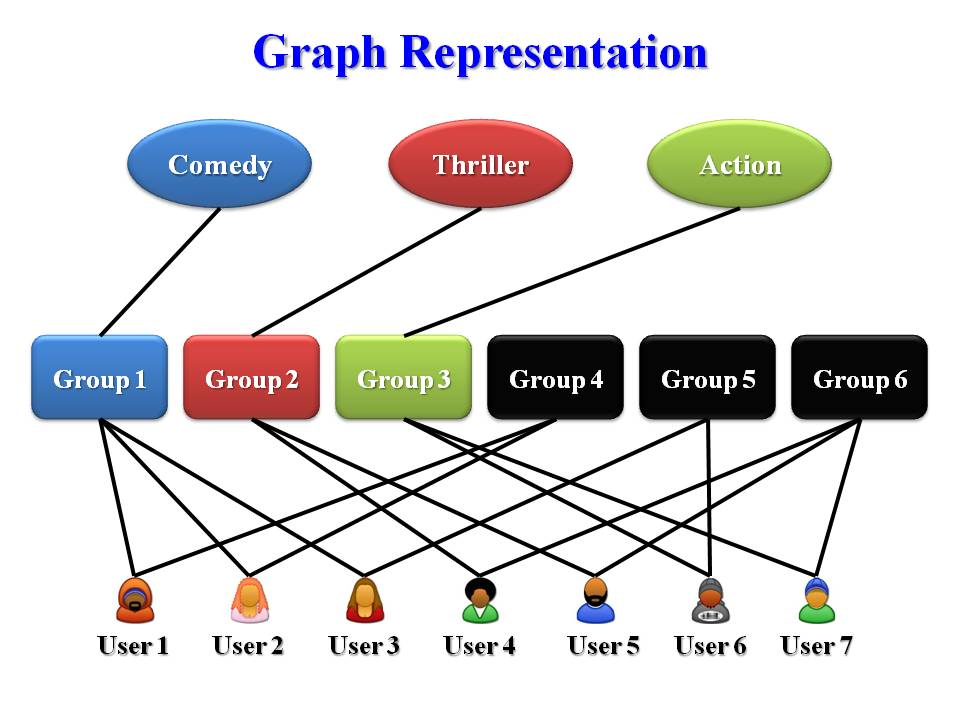
This problem cannot be solved by simple majority voting because the correspondence between the cluster ID and the class label is unknown, and the same cluster ID in different clustering models may represent different clusters. To achieve maximum agreement among various models, we must seek a global optimal prediction for the target objects. To tackle this problem, we propose to summarize the base model outputs using a bipartite graph in a lossless manner, as shown in the figure above. To reach maximum consensus among all the models, we define an optimization problem over the bipartite graph whose objective function penalizes the deviations from the base classifiers' predictions and the discrepancies of the predicted class labels among nearby nodes. We solve the optimization problem using a coordinate descent method and derive a global optimal label assignment for the target objects, which is different from the result of traditional majority voting and model combination approaches. The proposed method can be applied to more complicated situations. For example, it can work in the scenario when each object has a probabilistic label assignment, or each object has multiple labels to describe its category, or some predictions are missing from each source.