CSE 463/563, Spring 2005

Satisfaction of a Quantified WFF

Last Update: 4 March 2005

Note: or material is highlighted

In case my explanation in lecture of the definition of satisfaction for a quantified wff wasn't clear, here it is at greater length (for a finite case, which may make it easier to understand, and can be done "wolog", i.e. "without loss of generality").

Suppose our domain, $D$, contains the following items:

$$d_1 , \ldots , d_{200}$$

Suppose our language has these variables:

$$x_1, \ldots , x_{100}$$

The definition of satisfaction for a universally quantified wff is:

$$\Im ,\mu \models \forall v.\alpha ~~\mbox{iff}~~ \Im ,\mu... ...\mu ^\prime ~\mbox{that differ from}~\mu~\mbox{at most on}~v.$$

E.g., suppose $v$ is the variable: $x_{50}$
and $\alpha$ is the wff: " ${x_{50}}^2 = x_{50} * x_{50}$"

Consider the set of all variables: $\{x_1 , \ldots , x_{50}, \ldots , x_{100}\}$

Consider what set of members of $D$ we get by applying a variable assignment $\mu$ to all the members of this set:

$$\{\mu (x_1 ), \ldots , \mu (x_{50} ), \ldots , \mu (x_{100} )\} \subseteq D$$

Let's say that this set = $\{d_1 , \ldots , d_{50} , \ldots , d_{100} \}$.

Now consider all $\mu ^\prime$ that differ from $\mu$ at most on $x_{50}$. Suppose they are $\mu _1 , \ldots , \mu _{300}$.

(It may be that $\mu_{301} ,\ldots , \mu_{1000}$ differ from $\mu$ on other variables, too, so we don't consider these at all!)

Note that our $\mu$ above is one of these 300 $\mu ^\prime$ (because all the $\mu ^\prime$ differ at most on $x_{50}$, meaning that they might not differ on $x_{50}$ at all). For convenience, let's say that our $\mu$ above is $\mu _1$.

So consider what all these $\mu ^\prime$ do to the set of all variables; they map them into sets of elements of $D$ as follows:

$$\begin{eqnarray*} \mu _1&:&\{\mu _1 (x_1 ), \ldots , \mu _1 (x_{50} ), \ldots , ... ...), \ldots , \mu_{300} (x_{50} ), \ldots , \mu_{300} (x_{100} )\} \end{eqnarray*}$$

Note, in particular, that $\mu _1$ gives us: $\{d_1 , \ldots , d_{50} , \ldots , d_{100} \}$. What about the others? Well, each differs from $\mu$ (or $\mu _1$) at most on what it does to $x_{50}$, so we get the following:

$$\begin{eqnarray*} \mu_1&:&\{d_1 , \ldots , d_{49} , d_{50} , d_{51} , \ldots , d... ...:&\{d_1 , \ldots , d_{49} , d_{77} , d_{51} , \ldots , d_{100}\} \end{eqnarray*}$$

I.e., they are all alike on the first 49 variables and on the last 50 variables, but they can vary wildly on good old $x_{50}$.

Now, according to the definition, if all of these $\mu ^\prime$ satisfy " ${x_{50}}^2 = x_{50} * x_{50}$", then our original $\mu$ will satisfy " $\forall x_{50} [ {x_{50}}^2 = x_{50} * x_{50} ]$".

But to decide if a given $\mu ^\prime$ satisfies " ${x_{50}}^2 = x_{50} * x_{50}$", we can ignore what it does to everything except $x_{50}$.

(We can do this for 2 reasons: First, they don't differ on the other variables. Second, our wff only contains that one variable, so that's the only one we care about.)

On $x_{50}$, each $\mu ^\prime$ differs. Does each one satisfy " ${x_{50}}^2 = x_{50} * x_{50}$"? Sure! Here's the proof:

$$\begin{eqnarray*} &{d_{50}}^2=d_{50} * d_{50}\\ &{d_1}^2=d_1 * d_1\\ &\ldots \\ &{d_{77}}^2=d_{77} * d_{77} \end{eqnarray*}$$

So: all the $\mu ^\prime$ that differ from mu at most on $x_{50}$ satisfy " ${x_{50}}^2 = x_{50} * x_{50}$", so $\mu$ satisfies " $\forall x_{50} [ {x_{50}}^2 = x_{50} * x_{50} ]$".

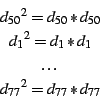
And similarly, "mutatis mutandis" (as mathematicians say; i.e., changing what needs to be changed), for the existential quantifier.