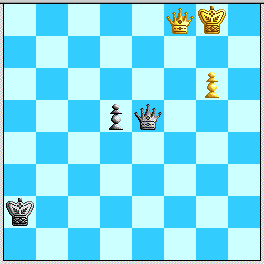
Diagram 1: Position "G".
All diagrams have been cut-and-pasted from MacChess 5.0.1 using Screen Catcher 1.0.

Diagram 1: Position "G".
All diagrams have been cut-and-pasted from MacChess 5.0.1 using Screen Catcher 1.0.
This position (possibly with Black's King on other, better squares) is the Kilimanjaro over the landscape of the entire endgame after 54...b4! The Kasparov-Alterman analysis file reaches it after 58...Qf5 59. Kh6 Qe6 60. Qd1+ Kb2 61. Qd2+ Kb1 62. Qd4 Ka2 63. Kg5 Qe7+ 64. Qf6 Qe3+ 65. Qf4 Qg1+ 66. Kf6 Qb6+ 67. Kf7 Qb7+ 68. Kg8 Qc8+ 69. Qf8 Qe6+ 70. Kg7 Qe5+ 71. Qf6 Qc7+ 72. Qf7 Qe5+ 73. Kg8 Qb8+ 74. Qf8 Qe5, and now they give "75. g7 G#" and claim +/-. Let us re-number move 75 as "1". The following analysis is offered as proof that this +/- claim is mistaken, and that Black holds the draw with or without 1. g7 (which is what K-A properly call "G").
[Status 11/11: completely done! I now claim that any defense listed here, whether labeled "primary" or "secondary", holds for Black, and that the lines given exhaust all reasonable White tries. The companion "Position G Extra" file will consider losing defenses and other cases. Meanwhile, Irina's people are collecting all this analysis into ChessBase and PGN format.]
The first of the following three branches is the line that Kasparov and Alterman give. Evidence that they intend it to be distinctive comes by comparing the form of Position G that White appears able to force in the 56...Qe3 line: 57. g6 d5 58. Qa4+ Kb1 59. Qb5+ Ka1 60. Qa6+ Kb1 61. Kf7 Qf4+ 62. Qf6 Qc7+ 63. Qe7 Qf4+ 64. Kg8 Qb8+ 65. Qf8 Qe5. The only difference is that Black's King is on b1, but this is enough to prevent White from checking high on the a and b files (after 1. g7 d4). Or: 61. Qf7 Ka1 62. Kf8 Qc5+ 63. Qe7 Qc8+ 64. Kf7 d4 65. Qe1+ Kb2 66. Qf2+ Kb1! 67. g7 Qd7+ 68. Kf6/g6 Qd8/g4+ 69. Kg6/f6 d3 looks fine for Black. Kasparov stated that he did not know a win against 56...Qe3 (but later to Sport Express that he expected to find one). Hence branch I. can be identified as the critical one, and this appearance seems reflected in the actual analysis as well.
Before going into these branches, we should identify the winning plans that are shown in their file. Some of them are at the label "G#" and some are in other places, including the conclusion of their entire main line. What they give includes:
These lines and ideas certainly show how thin the line between survival and death is for Black. They are basically all that the Kasparov-Alterman analysis gives, except for cases where Black's Queen is on f6 or is far away, or Black's King is on c2 or d1, a gap that begs for explanation. Nevertheless, we shall answer White's menace with several key defensive ingredients:
In addition to Main Defenses, we also give some Secondary Defenses. The latter show all (other) lines White would have to refute in order to demonstrate a win. None of these defenses is addressed at all in the Kasparov-Alterman file! However, because it appears that Black really does need the ...Qg5+! idea in Line I.D(a1) to hold (irrespective of the "secondary defense" that was busted by Club Kasparov and replaced by "Spy49" with one I prove to hold), and because the Kasparov-Alterman file embodied a belief that Black had to play 1. g7 d4 2. Qa8+ Kb2 3. Qb7+ Kc1(?), this can be identified as the most critical line and perhaps what was overlooked. In the companion file "PositionGextra.html" we will give White's clever win against 3...Ka3 here and other winning and drawing cases that may complete the entire theoretical picture of g7 vs. d4 (and b7 vs. e4) endings.
Part I.
1. g7 d4 2. Qa8+ Kb2 3. Qb7+ Ka1!.
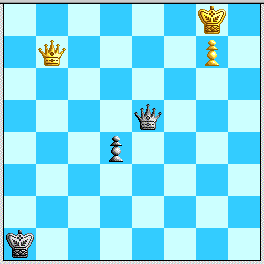
Diagram 2: the jumping-off point from Kasparov-Alterman.
White's main tries are listed in order of convenience for this presentation rather than danger. In lines A and B Black fundamentally has only one defense, but those defenses seem shortest and surest, respectively---line B was known from early work on 58...Qe4. Lines C and D each have one-or-two sub-lines that are marked critical for Black's survival, together with a bunch of other sub-lines that Black can mix-and-match (and where White would have to bust most of them to win). The lines are:
A. 4.
Qa6+ Kb2 5. Kf7 (5. Kf8 transposes after both 5...Qb8+ and
5...Qf5/f4+, and 5. Kh7 is included as well) Qc7+!
Yes, Black's 5...Qc7+ is an only-move, as 5...Qf4/f5+? 6. Qf6 sets up the winning Pin Battery, or 5...Qh5+? 6. Qg6 Qd5+ 7. Qe6 Qb7+ 8. Kf6 Qf3+ 9. Ke7 Qb7+ 10. Qd7 Qe4+ 11. Kd6! wins as in the 58...Qe4 lines. But now 6. Kf8 Qb8+ 7. Ke7 Qc7+ 8. Kf6 Qf4+ 9. Kg6 (Ke6 Qh6+) Qg3+! demonstrates that White can do no better than 10. Kh7 Qh3+ 11. Qh6 Qf5+ 12. Kh8 Qe5. This position also deserves a diagram,

Diagram 3a: "Averbakh study" plus pawn on d4. Draw.
This position and its variants with Black's king on a1 or other squares are important, but they do not represent progress for White. Now 13. Kh7 Qf5+ just repeats, and 13. Qd2+ Ka1 (or ...Ka3!?) 14. Qd1+ Kb2 15. Kh7 stops the ...Qh5+ perpetual but allows a different one with 15...Qf5+. And 13. Qb6+ Ka1 just gives White fewer options with his King on h8 as he has with it on g8. For this last point and others it is important to note that all quiet Queen moves can be met by ...d3! For instance, 13. Qh4 d3 14. Kh7 Qf5+ 15. Kh6 Qe6+ 16. Kg5/h5 Qe7/f7+ =, or 13. Qh3 d3 14. Kh7 Qe4+ 15. Kh6 Qc6+ 16. Kg5/h5 Qd5+ =. (In Part II we shall see Black survive a more difficult version of this with Black's King on a2.) Black's Queen on e5 prevents any imminent "Hogtie" danger, and all positions with Qxd3 are EGTB= even with White to move. (We will later find lines in II-III where Black gets in ...d3 and is still in danger, owing to a2 being a poor square for the King.) Finally, 11. Kg8, 12. Kg8, and 12. Qg6 Qh3+ 13. Kg8 are all met by ...d3!, with equality.
That finishes line A.
B. 4. Qa6+ Kb2 5. Qb6+ Ka1 6. Kf7. [There is no independent significance to 6. Kf8 since 6...Qf5+ 7. Ke7/e8 Qe5+ forces White to go back. And 6. Kh7 leads to variations of the last ones that make no great difference: it suffices to consider (i) 6...Qh5+ 7. Qh6 Qf5+ 8. Kh8 Qe5 9. Qc1+ Ka2, and White cannot exploit the bad position of Black's king because of 10. Kh7 Qf5+(!), or 10. Qc4+ Ka1 11. Kf7 Qf5+ 12. Ke7 Qe5+ (no Qe6 interposition now), with immediate perpetual check in both cases; and (ii) 8. Qg6 Qh3+ 9. Kg8 d3!, where even though Black's Queen and King are on the edge White cannot take advantage: 10. Qf6+ Kb1 11. Qd4 is not "Hogtie" (e.g. ...d2 12. Qxd2 is not check and is EGTB=), and 11. Qb6+ Kc2 12. Qc5+ Kb1! is not even as good for White as lines arising out of 51...Ka1 or other lines we shall see.]
After 6. Kf7 Qf5+ the only independent move is 7. Qf6, and now ...Qd7+ sets up the "Known Pattern" that was long ago known to hold in lines with 58...Qe4. We demonstrate that Black already has a perpetual check or forces a position with ...Qe5 pinning g7 to h8 of the kind we have already considered. The ideas are:
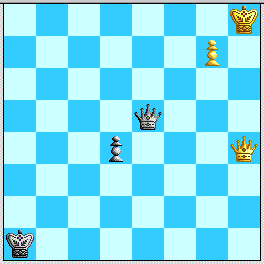
Diagram 3b: Averbakh study with White Queen on h4, Black King on a1. Draw.
White likewise has strictly fewer options than in continuations available in Part II, since all squares reachable from h4 are reachable from f2 or g2 (or f1,g1,h1) after checks in those lines. For example, 15. Qg4 d3 16. Kh7 Qh2+ 17. Kg6 Qd6+ 18. Kg5 Qd8+ 19. Kf4/h5 d2 is nothing for White.
C. 4. Qa7+ Kb2
Here 4...Kb1?! by Black probably loses---and seems to have no independent significance as White achieving Qf6 will beat that too, owing to a later pin along the b1-h7 diagonal as above.
(a1) 5. Kf8 Qf6+ 6.
Qf7.
(a2) 5. Kf8 Qf6+ 6. Ke8.
(b1) 5. Kf7 Qf5+ 6. Ke7 Qe5+ 7. Kd8 Qd5+ 8.
Qd7.
(b2) 5. Kf7 Qf5+ 6. Ke7 Qe5+ 7. Kd8 Qd5+ 8.
Kc7.
(a3) 5. Kf8 Qf5+ 6.
Qf7.
(a4) 5. Kf7/f8 Qf5+ 6. Ke8 Qc8+!?
(a1) 5. Kf8 Qf6+ 6. Qf7 Qd8+ 7. Qe8 Qf6+ 8. Kg8 d3=, e.g. 9. Qb5+ Kc2 10. Qc4+, and while 10...Kd2 11. Qd5 or 10...Qc3 11. Qe4 might give White hope to play on, there is nothing wrong with 10...Kb2(!), since not only 11. Qxd3 but also 11. Qd5 d2 12. Qxd2+ are EGTB= (6K1/6P1/5q2/8/8/8/1k1Q4/8+b), the latter even after the horrid 12...Kb3??!
(a2) 5. Kf8 Qf6+ 6. Ke8 (some subtle menace here!) Qe6+ 7. Qe7 Qg8+!, and now:
(a2i) 8. Kd7? gives Black the luxury of a choice between 8...d3 and 8...Qd5+. On 8...d3, 9. Qf8 Qd5+ 10. K-moves d2=, or 9. Qb4+ Kc2 10. Qc5+ Kb1 is dismissible. (The only thing Black mustn't do is think that Qf8 d2 is OK---it's EGTB= with Black's King on a1 or b2 (6Q1/3K2P1/8/8/8/8/1k6/3q4+w), but not on b1(!) or c2.) And 8...Qd5+ 9. Kc7/c8 d3 10. Qf6+ Kc7 11. Qg6 Qc5+ is a perpetual since White cannot offer or allow the trade of Queens, as some other WT members pointed out.
(a2ii) 8. Qf8! Qe6+ 9. Kd8.
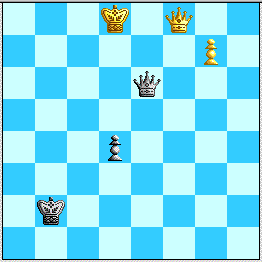
Diagram 4: Strange danger for Black.
With Black's pawn still on d4 Black has to sweat---the White Queen is less out of play on f8 than it looks. Indeed, if White's King ever reaches b6, it appears that Black is a goner(!), as White can maneuver via c5 to reach a5 when Black cannot reply ...Qd5+, and ...Qe5+ Ka4 or ...Qa1+ Kb5 become the end. (My main draw-claim post actually stepped into this by continuing 9...Qd5+ 10. Kc7 Qc4+(??) 11. Kd6(??) Qa6+ 12. Kd5 Qb5+, since I merely wanted to emphasize the main point that the interposition 13. Qc5 loses the pawn to ...Qd7+, but 10...Qa5+! is obviously a better-motivated way to reach a6 anyway.) Oddly enough the key to Black's survival is the ability to check on b7, which is a losing check if White can interpose on d7.
The following is a full proof of perpetual check by "Correspondence of Squares". For each square k that can be occupied by White's King, I give a list of squares q,q'... such that Black is OK if her Queen checks from any one of them. Thus to establish the proof, one must verify that
(for all possible White
King squares k1, and for *all*
q1 on the k1-list)
(for all
k2 such that
k1-k2 is legal if Black checks
from q1)
(there
exists q2 on the k2-list such
that q1-q2 is legal).
Note especially the cases where only one check is given---where this is important they are marked "!". The lists can be minimized a little---e.g. Black can never be forced to check from e2 in response to Ke6---but I wanted to show the relevant options. For the squares not given, the conclusion is that White's King can never reach them. NA means "does not apply", and squares shown in parentheses are also OK but not part of the proof.
WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on -- -------- -- -------- -- -------- -- -------- -- -------- a8 a6 a7 a5 a6 NA! a5 NA (a7) a4 a6 (c6) b8 b6 b7 b5 b6 NA!! b5 NA (b7) b4 b6 c8 c6 or a8 c7 a7 or a5 c6 a6 c5 a5! + c4 a6 d8 d5,b8,b6 d7 b7 or b5 d6 a6 or b6 d5 b5! ++ d4 NA e8 e6,c6,b5 e7 b7! e6 b3 or e2 e5 b5,e2 + e4 e2 f8 NA f7 b3,d5,f3 f6 c6 or f3 f5 f3! f4 f1 or f2 g8 d5,b3 * g7 NA g6 g2 or g3 g5 g2 g4 g2 h8 h3 ** h7 h3 h6 h3 or h4 h5 h3 h4 h2 or h1 Notes: * Just avoid Qf7 Qa8+? f3 f1 ** Any square on h-file is OK, but this is best. g3 g1 + On Kxd4 all Q-checks are EGTB= h3 h1 ++ So that Qc5 is met by ...Qd7+ winning the g-pawn. other squares NB: on Kd5 Black is OK also with ...Qd7+, ditto Kc5 Qa7+. are all NA.
White never gets a useful Queen interposition---Q.E.D. to finish line (a2).
(b1) 5. Kf7 Qf5+ 6. Ke7 Qe5+ 7. Kd8 Qd5+ 8. Qd7 Qg8+! (only move!) 9.
Kc7 (only move!) d3.

Diagram 5: Critical defense but solid: Black's Queen blocks and covers c4 while Black's King is near to help d3.
White's options seem all to be showable in one line: 10. Qb5+ Kc2 11. Qa4+ Kb2 12. Qd4+ Kc2 13. Qc5+ Kb1 14. Qf8 Qc4+ and 15...d2, draw.
(b2) 5. Kf7 Qf5+ 6. Ke7 Qe5+ 7. Kd8 Qd5+ 8. Kc7 Qf7+! 9. Kb6 (other
moves lose!) Qe6+ 10. Kb7 Qd5+!, or 10. Kb5 Qd5+ 11. Kb4 d3 12. Qa3+
Kb1 13. Kc3 Qe5+ 14. Kxd3 Qxg7=, or 12. Qb8 d2 13 Ka4 Ka1! -/+.
This is enough to constitute a complete defense in line I.C. However, the following alternatives are also thematic and interesting:
(a3) 5. Kf8 Qf5+ 6. Qf7 Qc8+ 7. Ke7 (7. Qe8 Qf5+
8. Ke7 Qe5+ repeats, or 8. Kg8 d3=) Qb7+! 8. Ke6 Qb3+ 9. Kf6 Qf3+ 10.
Kg6 Qg3+! 11. Kh6 Qe3+! 12. Kh7 Qh3+ 13. Kg8 d3=.
(a4) 5. Kf7/f8 Qf5+ 6. Ke8 Qc8+!? 7. Ke7 d3, and now:
(a4i) 8. Qf2+ Kc3! 9. Qf6+ Kc2 (no more
useful White checks) 10. Qg6 Qc7+ followed soon by Queen trade on g6
or e8 and ...d2=. Or 10. Qf8 Qc5+ 11. Kf6 Qd4+ and draw after
covering g8 with a check or trading Queens if White interposes or
just giving perpetual check, or 9. Qg3 Qc5+ 10. Ke6/f6 Qc6+ 11. Kf5
Qe4+ 12. Kg4 Qe4+, and the inability to stand a Queen trade means
White has nothing.
(a4ii) [Dewey Autry] 8. Qd4+ Kc2 9.
Qa4+ Kb2 10. Qa5. A good idea, covering d2 and preventing Black's
King from assisting because of a check on a2. However, White's
problem in any line like this with Black's King out of fire from g8
is the inability to offer a Queen trade. Black has only one check,
but it is good enough: 10...Qb7+ 11. Kf6 Qf3+ 12. Kg6 Qg2+ 13. Kf7
Qf3+ 14. Ke8 Qc6+, or 14. Kg8 d2!? 15. Qxd2+ and now even 15...Ka1
16. Qd4+ is EGTB=. Worth noting as the one exception to the rule that
White's Queen capturing and reaching d4 wins---Black's Queen on f3 or
f5 keeps White's King confined.
Line (a4) now has confirmation from Richard Maisiak ("Spy49") of giving 0.00 on Crafty as well. Lines (a3) and (a4) together remove Black's dependence on (a2).
This takes complete care of 4.
Qa7+.
D. 4. Kf7 Qf5+ (4. Kf8 Qf6+ 5. Qf7 Qd8+ =, or 5. Ke8 Qe6+ 6. Qe7 transposing into line B.) 5. Ke7, and now:
(a1) 5...Qg5+! [Peter
Karrer] 6. Ke8 d3.
(a2) 5...Qg5+ 6. Kd6 Qg6+ 7. Kc5 Qc2+! 8. Kb5
Qb1+! 9. Ka6 Qg6+! and now (i) 10. Ka7 d3 or (ii) Ka5 d3.
In line (a2) we note that 6. Ke6 Qg6+ 7. Ke5 Qg5+ 8. Kxd4 is EGTB=
(8/1Q4P1/8/6q1/3K4/8/8/k7+b),
and since the seven(!) holding checks include 8...Qd2+, Black is fine
after 8. Kxd4 in (a2) as well.
(b1) 5...Qe5+ 6. Kd8 Qg5+
7. Kc8 d3, which is also needed for 5...Qe5+ to be viable.
(b2) 5...Qe5+ 6. Kd8 Qg5+ 7. Qe7 Qa5+!
[Richard Maisiak as "Spy49"].
Note, however, that on 7. Ke8 Black has no better than to transpose
into line (a1) by playing 7...d3, which is what makes line (a1)
uniquely critical. The White win against 6...Qd6+ and 7...Qe5+ here
is even more delicate and beautiful than White's win against
58...Qe4, and is the crucial point about Qd7 being in
general a winning interposition. We consider the "a"-defenses
first:
(a1) 5...Qg5+! [Peter Karrer] 6. Ke8 d3.
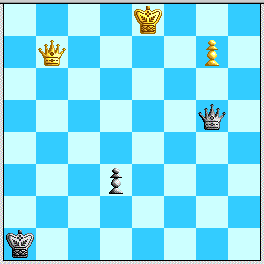
Diagram 6a: After 6...d3---apparently the single drawing resource that turns the entire endgame, perhaps millions of positions!
The amazing fact is that White's Queen is out of position for useful checks despite the distance between Black's King and Black's pawn. The same position with White's Queen on a7 and Black's King closer on b2 would be winning for White after 7. Qd4+!, but Black's King can duck away from squares that would let White win this tempo. White has:
(i) 7. Qa7+ Kb1! 8. Qb6+ Kc2 9. Qc6+ Kb2=.
(ii) 7. Qa6+ Kb2! rest as in (i).
(iii) 7. Qh1+ Kb2 8. Qh2+ d2=
(iv) 7. Kf8 Qf5+= since White cannot offer a trade of Queens.
Computer evaluations equipped with 5-piece EGTBs show "0.00"
here---so there should not be any need for further verification!
(a2) 5...Qg5+ 6. Kd6 Qg6+ 7. Kc5 Qc2+! 8. Kb5 Qb1+! 9. Ka6 Qg6+! and now (i) 10. Ka7 d3 or (ii) Ka5 d3 give us twin positions:
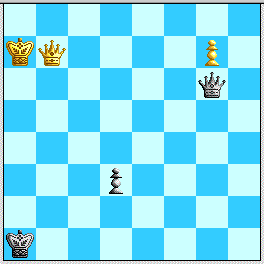
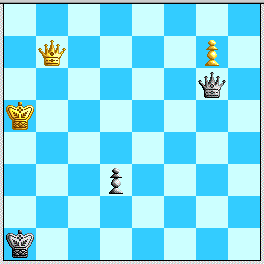
Diagrams 6b and 6c: two more cases where White's Queen is not effective on b7.
In both positions the only checking sequence is
11. Qh1+ Kb2! 12. Qh2+, and now Black avoids the temptation to play
12...Ka3? 13. Qe5! and instead plays 12...Kc1! 13. Qc7+ Kd1. Black
has been forced in front of the d-pawn, but White is completely
devoid of any useful moves to threaten anything! The only independent
tries seem to come from position (ii): 11. Kb4!? d2 12. Kc3, and part
of me wishes 12...d1=N+! were the only move to hold, but there is
nothing wrong with pitching the pawn by 12...Qf6+ 13. Kxd2 EGTB=. Or
11. Qa7/d7 d2 12. Qd4+ Kb1 13. Qb4+ Kc1 14. Qc4+ Kb1=. White's King
is just too far away to assist in a mate. (Note, however, that
7...Qg5+? would allow a pretty win by 8. Kb4! Qd2+ 9. Kb5! Qg5+ 10.
Ka4! d3 11. Qa8! +/-.)
This completes an entire Black defense in Part I.
Thus White cannot win with the moves given by the Kasparov-Alterman analysis.
We may as well handle the secondary lines (b1) and (b2) here as well.
(b1) 5...Qe5+ 6. Kd8 Qg5+ 7. Kc8 d3. Similar to
line (a1) and equally fine for Black.
(b2) 5...Qe5+ 6. Kd8 Qg5+ 7. Qe7 Qa5+! The aim of this defense is to
prevent White from interposing on d7 and from reaching the a8 corner.
Now:
(i) 8. Ke8 Qa8+!! (instead, 8...Qh5+? 9. Qf7! Qe5+ 10. Kd7 transposes
into the Kasparov-Alterman main winning line) 9. Kf7 Qf3+ 10. Ke6
Qb3+! 11. Ke5 Qe3+ 12. Kd6 Qa3+! 13. Kd7 Qa4+ and White can do no
better than 14. Ke6 Qb3+ 15. Kf6 Qf3+ 16. Kg6 Qd3+ 17. Kf7 Qf5+,
reaching the "known pattern" of line B.
(ii) 8. Ke8 Qa8+ 9. Kf7 Qf3+ 10. Qf6 Qb7+, and now the only option independent of Line B. is 11. Kg6 Qg2+! 12. Qg5 Qc6+ 13. Kh5 Qh1+! 14. Kg4 Qd1+! 15. Kf4 Qc1+ 16. Kf5 Qc2+ 17. Kf6 Qc6+, and the law of symmetry really does hold here.
(iii) 8. Qc7 Qa8+! 9. Ke7 Qe4+ 10. Kd6 Qg6+ 11. Kd5 Qg2+! 12. Kc5 Qc2+ 13. Kb5/b6 Qb3+ 14. Ka6! d3!? and once again Black wriggles out of trouble, just barely avoiding a check on f2 when it would be killing: 15. Qe5+ Kb1! (not ...Ka2 16. Qd4! Hogtie) 16. Qd4 d2! (less dangerous living than ...Kc2?! 17. Qc5+ Kd2 18. Qf2+ Kc3, maybe 18. Qf8 is +/-, hmm...) 17. Qxd2 Qc4/e6+ EGTB= (8/6P1/K7/8/8/1q6/3Q4/1k6+b).
The full proof of a draw in (b2) is the most complicated corresponding-squares argument in the entire endgame, since it involves White's Queen possibly being on e7, c7, c8, and g5, with the e7 and g5 cases being apart from the "Known Pattern". While not needed to prove a draw in Position G itself, this line also refutes White tries in other parts of the whole 58...Qf5 endgame, and rounds out the picture of which interpositions win.
With White Queen on e7, BQ on a5 checking WK on d8: WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on -- -------- -- -------- -- -------- -- -------- a8 NA a7 NA a6 NA a5 NA 4th rank all NA. b8 NA b7 NA b6 NA b5 NA c8 a8 c7 a7 c6 NA! c5 NA! d8 a8 (a5)* d7 a4 d6 a3 d5 NA! e8 a8!! e7 NA e6 b3! e5 e3 f8 NA f7 f3! ** f6 f3 f5 f3 g8 ...d3 g7 NA g6 g4 or d3 g5 g3 h8 h3 h7 h3 h6 h3 h5 h3 * a5 is initial condition, and only chance for White to interpose on c7; then Black plays ...Qa8+! and reaches the last chart below. ** White may interpose on f6; then Black plays ...Qb7+! to next item: With White Queen on f6, BQ on b7 checking WK on f7: -------------------------------------------------- Any move other than Kg6 repeats or transposes into the "Known Pattern" of line I.B. Then on 1. Kg6 Qg2+!, the only new option is to interpose 2. Qg5, and after 2...Qc6+ we reach the next chart (note ranks go down now). With White Queen on g5, BQ on c6 checking WK on g6: WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on -- -------- -- -------- -- -------- -- -------- h8 NA g8 ...d3 f8 c8 e8 c8 + h7 h1! * g7 NA f7 d7 e7 c7 h6 NA! * g6 c6 f6 c6 e6 c6 h5 h1! ** g5 NA f5 c2! e5 c5 h4 h1 g4 d1 f4 c1 e4 NA! h3 h1 g3 g1 f3 NA! other squares NA. * Allowing White to play Kh6 and later interpose Qg6 would not lose if Black can reply ...Qc1+, but Black can prevent this headache. ** Now interposing 1. Qh4 achieves nothing after 1...Qd5+ 2. Kg6/h6 Qe6+ 3. Kh7 Qf5+ 4. Kh8 Qe5, leading back to Diagram 3b. + 1. Qd8 Qe6+ transposes to the "Known Pattern". With White Queen on c7, BQ on a8 checking WK on d8 (A very tricky line, in which Black must survive an "end-around" and funny Qc8 ideas too!): WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on -- -------- -- -------- -- -------- -- -------- -- -------- a8 NA!! a7 a2! a6 d3! a5 a3 a4 NA b8 g8!! b7 d5! ** b6 b3 b5 NA b4 NA c8 a8 c7 NA c6 f3! c5 c2 or a3 c4 c3 d8 a8! * d7 d5 + d6 g3 or g6 d5 g2 or f3 d4 NA e8 g8 or e6 e7 e4 e6 g4 or g6 e5 g3 or h2 e4 e2 ++ f8 f6 f7 f5 f6 h4! f5 h5 f4 h2 * Now 1. Qc8 Qa5+! either repeats or leads to a somewhat tricky line: 2. Ke8/e7 Qe5+ 3. Kf7 Qf4+! (...Qh5+? 4. Kf8! is trouble) 4. Kg6 Qg3+ 5. Kh7 (5. Kf6 Qh4+ makes White turn back). Now 5...Qh4+!? 6. Kg8 d3 7. Qc3+ Ka2! 8. Kf7 Qf4+ is probably OK, because (i) Kxd3 Qg3+ is EGTB=, (ii) a Qc7 interposition can be met by ...Qd5+ and ...d2, and (iii) 9. Ke7 Qe4+ 9. Kd6 Qg6+ 10. Kc5 Qg5+ 11. Kb4/c4/d4 d2! leaves White with no mate and no winning Qd4 or Qc4+! interpositions either (conclusion: Qc3 is not a winning "Hogtie"). However, most "sensible" seems 5...Qh2+ 6. Kg8 Qe5(!), and "son of a G" we have another version! This one seems to leave White with no notable new options other than (i) 7. Qc1+ Ka2 8. Qc6 d3 9. Kf7 Qf5+ 10. Qf6 (10. Ke7 Qe5+ repeats), where the "Known Pattern" draw of Line I.B applies after 10...Qd7+ just as with Black's King on a1 (since White never gets a white-square interposition and Black does not need to check on a2---this is Line III.D below), and (ii) 7. Qc1+ Ka2 8. Qc4+ Ka1 9. Kf7 Qf5+, draw. ** Now Qc6 Qf7+ repeats. + Now Qd6 Qb7+ repeats. ++ All Kxd4 possibilities are meetable by ...Qd1+ EGTB=.
Part II. White's Queen goes K-side.
1. g7 d4, moves without 2. Qa8+ (incl. also 2. Qa8+ Kb2 3. Qg2+ and 2. Qa8+ Kb2 3. Qb7+ Ka1 4. Qh1+)
The possibilities here appear to be (only) the four appearing in the line 2. Qf2+ Ka1 3. Qf1+ Kb2 4. Qg2+ Ka1 5. Qg1+ Kb2, plus 5. Qh1+ and 5. Qh3, 2. Qf7+, and non-checking moves at Move 2 that attempt to exploit the initial bad situation a2 of Black's King---of which only 2. Qf3 appears to present any real danger. [The following is still a little rough but looks complete.]
A. 2. Qf2+ Ka1 3. Kf7 Qd5+ 4. Kf6 Qd6+ 5. Kf5 Qd7+ (or 5. Kg5 Qe5+), and White can do no better than 6. Kg6 Qe6+ 7. Qf6 Qg4+ transposing to the "known pattern" line I.B.
B. 2. Qf2+ Ka1 3. Qf1+ Kb2 4. Kf7. Now allowing a Qf6 interposition would be a loss, but Black takes advantage of the fact that White's Queen on f1 is not covering g3 and not guarding g7 either: 4...Qc7+! 5. Kg6 Qg3+! 6. Kf6 Qd6+! The one asymmetrical element compared to line I.A is that 7. Kf5 cannot be answered by a skewer the f-file (since White's pawn guards f8), but Black has two ways to hit back: 7. Kf5 Qd7+ 8. Kg6 Qg4+ 9. Kf6 d3!, when 10. Qxd3 is EGTB= and 10. Qf2+ Kb1 (or ...Kc1) transposes into lines known to hold from the 51...Ka1 analysis, and perhaps simpler: 7...Qd5+ and 8...d3.
C. 2. Qf2+ Ka1 3. Qf1+ Kb2 4. Qg2+ Ka1 (...Ka3!?) 5. Kf7 Qf5+ 6. Ke7 Qe5+ 7. Kd7.
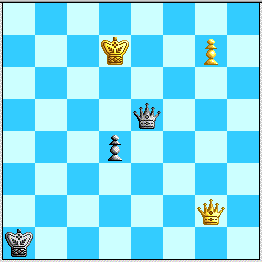
Diagram 7: Black follows White's King counterclockwise.
Black's idea is to pivot around and get behind the White King once it commits to being south of the h1-a8 diagonal, not allowing White to interpose (unless Black could immediately win the g-pawn): 7...Qf5+ 8. Kd6 Qf6+ 9. Kc7 Qe7+ 10. Kc6 Qe6+ (10. Kb6 Qd8+!) 11. Kb5 Qd7+ (White cannot interpose) 12. Kb4 Qd6+ 13. Kc4 Qc7+ (...Qa6+ might allow White to run back to the K-side starting with 13. Kc5) 14. Kd3 Qc3+ 15. Ke2 d3+ followed by trading Queens on g2 and ...d2. Or 9. Kd5 Qf5+ 10. Kc4 Qc8+ heads to the same general place; while 8. Kc7 Qc5+! is another case of an interposition 9. Qc6 allowing ...Qe5+ winning the pawn. In the latter case, 9. Kb8 Qd6+! 10. Ka7 Qc5+ 11. Ka6 Qd6+ 12. Kb5 Qb8+ 13. Kc5 Qc7+ is typical of Black having enough room to check and not let White's King escape. In all these cases Kxd4 is EGTB=. Here is the general "correspondence of squares":
WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on WK BQ OK on -- -------- -- -------- -- -------- -- -------- -- -------- a8 a6 or c8 a7 c5 a6 d6 a5 c5 a4 c4 or a6 b8 d6 or d8 b7 d7 or b5 b6 d8! b5 d7! b4 b6 or d6 c8 e8 or e6 c7 e5 or e7 c6 e6 c5 c7,e7,e5 c4 c7 or c8 d8 d6 or f6 d7 f5 or f7 d6 f6 d5 b7 or f5 d4 NA * e8 e6 or e5 e7 e5 e6 NA e5 e5 NA e4 c6 f8 f6 or f5 f7 f5 f6 NA f5 NA f4 NA ** * All Kxd4 cases have multiple EGTB= checks. ** The rest is a3--Qc3+, b3--Qb6+ or Qc3+, d3--Qc3+ (as above), and c2--Qb2+.
D. 2. Qf2+ Ka1 3. Qg1+ Kb2 4. Kf7 Qf5+. Black has an immediate perpetual since White has no control over either h5 or f5--a5.
E. 2. Qf2+ Ka1 3. Qf1+ Kb2 4. Qg2+ Ka1 5. Qh1+ Kb2 6. Kh7 Qf5+ 7. Kh6 Qf6+, or 6. Kf7 Qf5+ 7. Ke7 Qe5+. White gets no further since g7 is unguarded.
F. 2. Qf2+ Ka1 3. Qf1+ Kb2 4. Qg2+ Ka1 5. Qh3!? d3 6. Kh7 Qe4+ 7. Kh6 Qf4+ 8. Kg6 Qd6+ 9. Kf7 Qc7+ (or even ...d2) 10. Kf6 Qd6+= as White cannot usefully interpose. Or 5. Qh1+ Kb2 6. Qh3 d3, no better for White.
G. 2. Qf7+ Ka1 3. Kf8 Qb8+! 4. Qe8 Qf4+ 5. Ke7 Qe5+ repeats, or 4. Ke7 Qb7+! setting up the previously-seen "drawing perimeter" on b7,b3,f3,g3,h3 and ...Qe3+ after Kh6. And 3. Kh7 Qh2+ 4. Kg6 Qg3+ leads to the same thing.
H. 2. Qf3 d3! 3. Kf7/h7 Qc7/h2+ 4. Kg6 Qd6+. Up to here it is pretty much forced, since 3. Qxd3 is EGTB=, and 3. Kf8 Qd6+ 4. Ke8 Qe5+ is no different. Now on 5. Kf5 Qd7+ 6.Kf6 Qd6+ and 5. Kg5 Qe5+ 6. Kh6 Qd6+ White makes no progress, so forced is 5. Qf6 Qg3+.
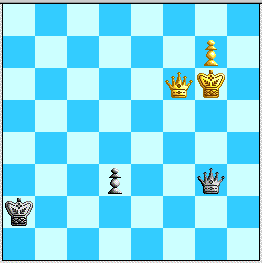
Diagram 8. White cannot take advantage of Black's King being on a2.
Now any King move can safely be met by 6...d2 since White has no forks or good square-covering checks and Black controls the 3rd rank. So 6. Qg5 Qd6+, and now 7. Kh7 Qd7! is no problem for Black, e.g. 8. Qh5 d2 9. Kh8 Qd4. (Indeed, the position is EGTB= even without the Black pawn!) Instead White can try to run his King down the board, but 7. Kf5 Qc5+! 8. Kf4 Qc1+! 9. Kg4 Qg1+ 10. Kh5 Qh2+ stops that cold, and after 11. Qh4 Qe5+ 12. Kg6 Qe8+! 13. Kh7, Black just plays 13...d2! for equality. The last try is 7. Kf7 Qd7+ 8. Qe7 Qd5+!, when White cannot gain by interposing on e6. Since White can't check on a4, any King move here is just met by ...d2 and =.
J. 1. g7 d4 2. Kf7!? This is like Line I.Ca2(ii) but with Black's King on a2 not b2. The same correspondence-of-squares perpetual check is valid here (beginning 2...Qd5+ 3. Ke7 Qb7+! or 3. Kf6 Qf3+!), but actually Black is not in danger from White's King getting to b6 now, so any careful sequence of checks is good enough to draw.
Are any other non-checking moves worthy of attention? They can all be met by ...d3! The best such move would seem to be the illegal 1. Qf8-g6, with the idea that on 1...d3 2. Kh7 Qh2+ 3. Qh6 Black has no more checks, but then 2...Qc7! seems fine, since 3. Qxd3 Qh2+ is still EGTB=, and 3. Kh6 Qh2+ 4. Qh5 Qf4+ 5. Kh7 Qe4+ 6. Kh8 no longer works as an idea since Black has 6...Qd4. (Diagrams 3a and 3b above do not have Black's King on a2.)
Part III. Moves without 1. g7.
Black's idea here is to play as in Parts I-II in response to checking moves, after which g7 can be answered by d4 if Black does not already have a perpetual check by ...Qe8+. Black just has to avoid special traps. Coming in the plethora of White options seems frightening, but with Parts I and II down there is not much here---and Line A. is the only one I once feared and the only one of this kind mentioned in the Kasparov-Alterman analysis.
A. 1. Qf2+ Ka1! (they give ...Kb1, why?) 2. Qa7+ Kb2 3. Qb6+. Put Black's Queen anywhere but e5 and this is deep trouble, but now 3...Ka1 4. Kf7 d4 leaves White nothing more than transposition into Part I by checks on a6,b7,a7 if desired and then pushing g7.
B. 1. Qf3 d4 2. g7 d3! or 2. Kf7 d3 (...Qc7+ looks fine too), transposing into II.H in both cases.
C. 1. Qf2+ Ka1 2. Kf7 d4 3. Qf1+ Kb2 etc. also transposes into Part II lines.
D. 1. Qf2+ Ka1 2. Qg1+ Kb2 3. Qg2+ Ka1 4. Qh1+ Ka2! (not 4...Kb2?? 5. Qh8! +/-) 5. g7 d4 6. Qc6 d3 7. Kf7 Qf5+, and since 8. Ke7/e8 Qe5+ repeats, White has nothing better than 8. Qf6, when 8...Qd7+ 9. Kf8 Qc8+ 10. Ke7 d2 and 9. Kg6 Qg4+ 10. Kh6 d2 demonstrate White's inability to escape the "Known Pattern" checks. (Thus with Black's King on a2, White's Queen is more dangerous on f3 than on c6.)
E. 1. Qf7 Qb8+ enables Black to repeat all the way back to Position G again.
F. 1. Qg7 Qb8+! 2. Kh7 Qh2+ 3. Qh6 Qc2! is fine for Black: 4. Kg8 Qc8+ repeats the moves leading up toward "G" in the Kasparov-Alterman main line, and 4. Qf4 d4 5. Kh6 d3 6. g7 Qc6+ 7. Kg5 Qd5+ 8. Qf5 Qg2+ 9. Qg4 Qd5+ is a draw via ...d2 as soon as White moves his King.
G. 1. Qc5 Qb8+ again forces White to repeat.
H. 1. Qa8+ Kb2 2. Qb7+ Ka1 3. Qa6+ Kb2 4. Qb5+ Ka1 5. g7 Qe6+ is a perpetual.
J. 1. Kf7 Qf5+ repeats.
I cannot see any other try for White in any of these lines.
DRAW.