UNIVERSITY AT BUFFALO, THE STATE UNIVERSITY OF NEW YORK
The Department of Computer Science & Engineering

STUART C. SHAPIRO: CSE 116 B

Readings

Riley Chapter 9

Introduction

A binary tree is a tree in which every node has at most two children, which are distinguished: one is the left child; the other is the right child. If a node has only one child, that is either the left child or the right child. Example

Node 1 is the root.
Nodes 2, 3, and 5 are branch nodes.
Nodes 4, 6, and 7 are leaves.
Nodes 1 and 2 have two children.
Node 3 has only a right child.
Node 5 has only a left child.

Numerical Properties of Full Binary Trees

A full binary tree is one in which for any level d, either all the nodes at level d are leaves, or all the nodes at level d have two children.

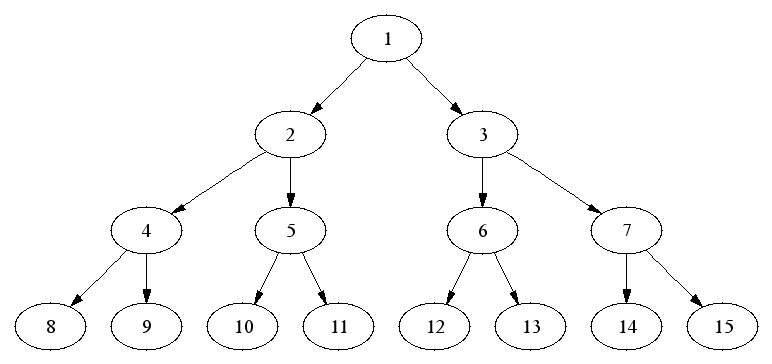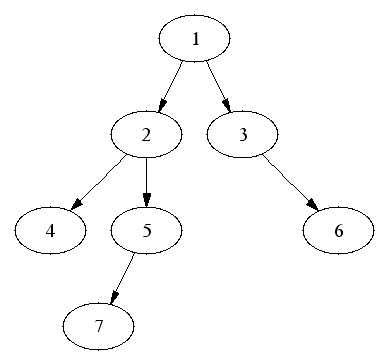
If the root is at level 0: each level, d contains 2d nodes; a tree of height h contains 2h+1-1 nodes. In binary: level 0: 1 =20 nodes level 1: 10 =21 nodes level 2: 100 =22 nodes level 3: 1000 =23 nodes Total: 1111 =24-1 nodes

Implementation

See BinaryTree.java for a recursive implementation of binary trees.

Traversal Algorithms

There are three standard algorithms for traversing (visiting the nodes of) binary trees: preorder; inorder; postorder. ("Pre", "in", and "post" refer to when the root is visited relative to the subtrees.)

1. Preorder Traversal
   Visit the root, then the left subtree, then the right subtree.

   Inorder Traversal

   Visit the left subtree, then the root, then the right subtree.

   Postorder Traversal

   Visit the left subtree, then the right subtree, then the root.

Example: Expression Trees

An expression tree represents an expression by storing an operator in the root, and its operand expressions in the two subtrees.
Inorder: ((5 * (10 - 4)) / (18 / (2 * 3)))
Preorder: / * 5 - 10 4 / 18 * 2 3
Postorder: 5 10 4 - * 18 2 3 * / / See the implementation of ExpressionTree.java
Notice that preorder and postorder notations do not require parentheses.

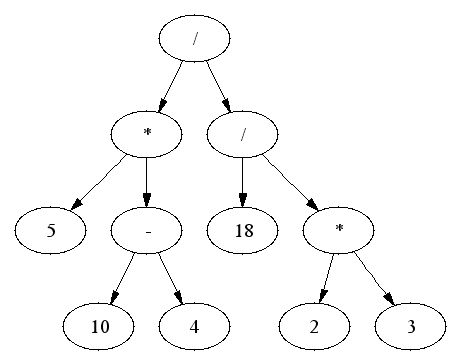
Pseudocode evaluator of postfix expressions:

int postfixEvaluator(TokenStream stream) {
    Stack stack;
    Token token;
    while (stream.hasNext()) {
        token = stream.next();
        if (token instanceof int) stack.push(token);
        else { // token is an operator
            opnd2 = stack.pop();
            opnd1 = stack.pop();
            stack.push(apply(token, opnd1, opnd2));
        }
    }
    return stack.top();
}

Stuart C. Shapiro <shapiro@cse.buffalo.edu>