UNIVERSITY AT BUFFALO, THE STATE UNIVERSITY OF NEW YORK
The Department of Computer Science & Engineering

STUART C. SHAPIRO: CSE 116 B

Readings

Riley Chapter 9

Introduction

A Heap is a binary tree with the following properties:

1. It is complete, i.e. full, except possibly for some right-most nodes at the highest level (at the bottom of the tree).
2. The value of the root is greater than (or equal to, if duplicates are allowed) the values of all other nodes.

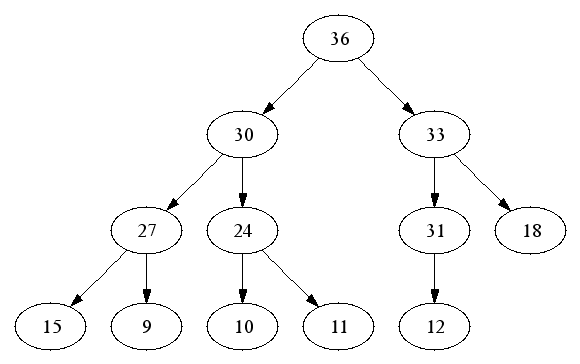
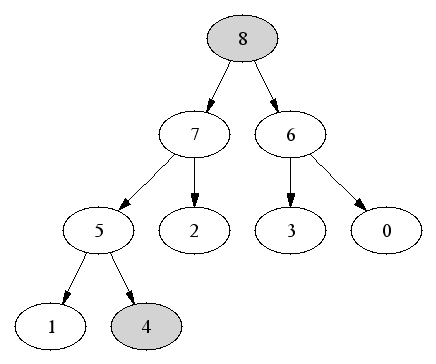
Complete binary trees are particularly easy to represent in arrays. Number the nodes by level:

Note that:

• the two children of node i are numbered 2i+1 and 2i+2;
• the parent of node i is (i-1)/2;
• there are no "gaps" in the array.

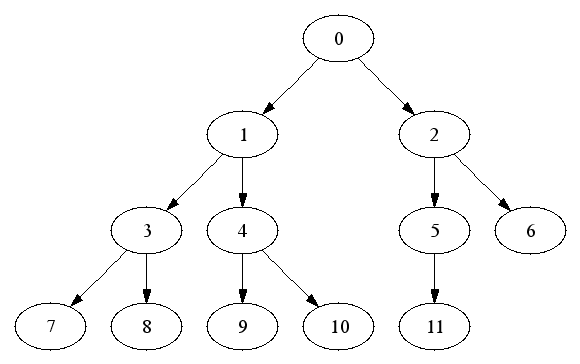
So any complete binary tree containing n nodes can be represented in an array, a of n elements, where a[i] contains the value of the i^th node, numbered as above.

Making a Heap

To turn an arbitrary complete binary tree into a heap, visit the nodes breadth-first (level by level, left to right == in order of their position in the array), and use the insertion algorithm (from the insertion sort) to "promote" each value up its branch. Running time is O(n log n).
Example [Riley, p. 410-411]:

Heap as Priority Queue

Insert by adding to end (as array), and promoting. Running time is O(log n).

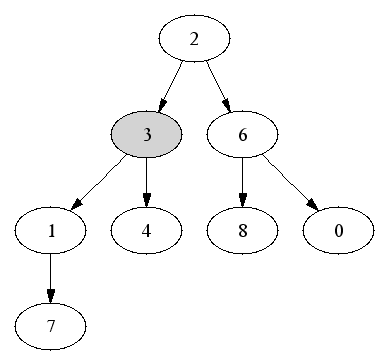
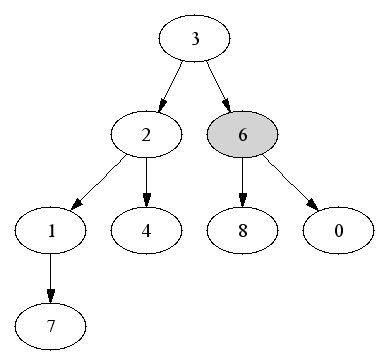
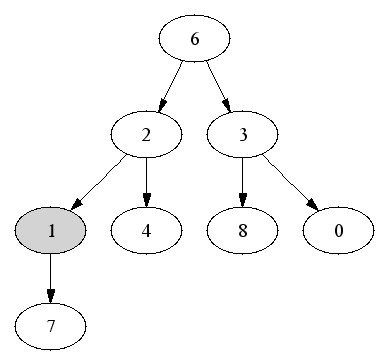
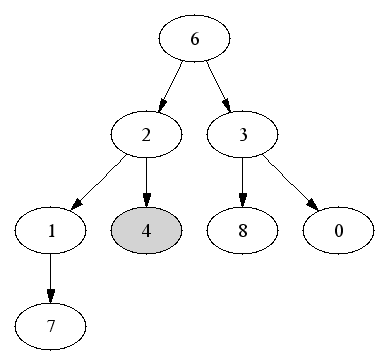
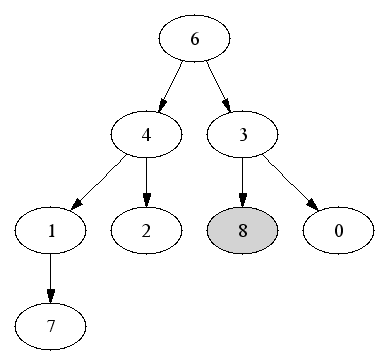
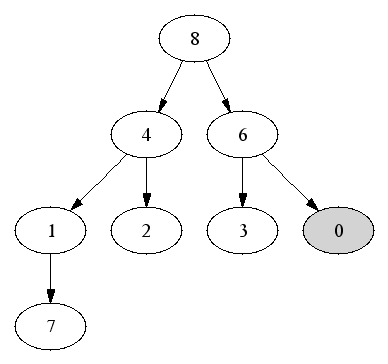
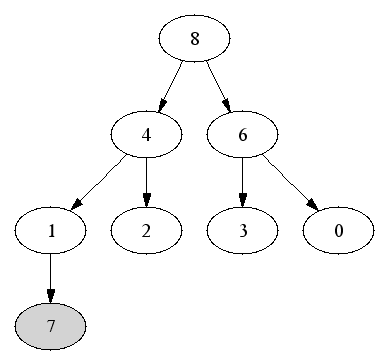
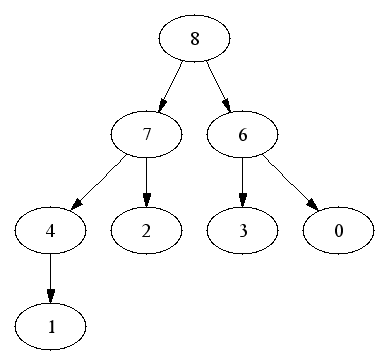
First element is the root (index 0). Running time is O(1).

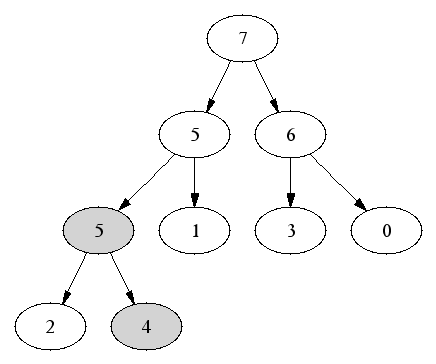
Delete and return first element.
Then go top-down to find correct position for value of old last node.
Fill an empty branch node with the maximum of the old last element and the child nodes.
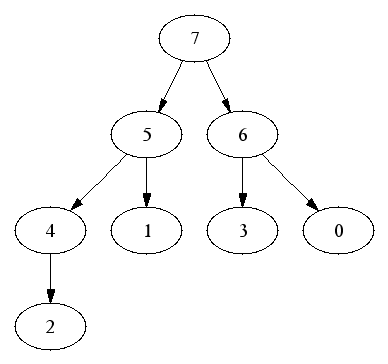
Running time is O(log n).

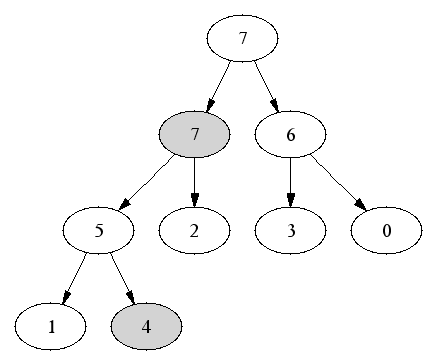
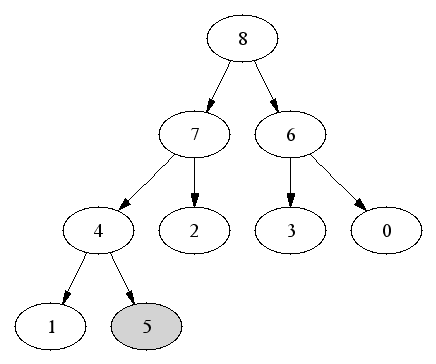
Insertion:

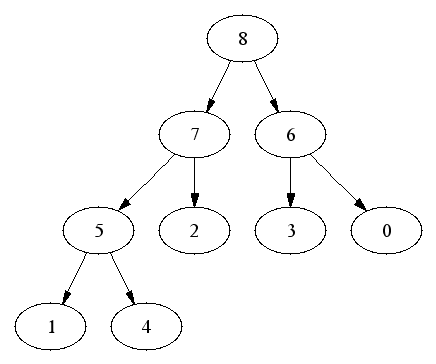
Deletion:

Heap Sorting

Given an array:

1. Make it into a heap.
2. While the heap is non-empty
   1. Let v be result of delete.
   2. Put v in old last position.

Running time is O(n log n).

Implementation

See Heap.java

Stuart C. Shapiro <shapiro@cse.buffalo.edu>