UNIVERSITY AT BUFFALO, THE STATE UNIVERSITY OF NEW YORK
The Department of Computer Science & Engineering

STUART C. SHAPIRO: CSE 305

Backus-Naur Form (BNF)

Named for John Backus and Peter Naur, though sometimes referred to as "Backus Normal Form". Developed by Backus as part of ALGOL 58 development, and modified by Naur as part of ALGOL 60 development.

Issue: How to describe a piece of source code, or other computer command or piece of language in general?

Notice submit instructions on course home page: submit_cse305 file

The submit_cse305 part is to be entered as a command exactly as shown, but the file part is to be replaced by an actual file name.

We can consider submit_cse305 file to be a command that is not yet finished---some of it needs to be replaced by a final (or terminal) string. The submit_cse305 part is already a terminal string; in fact, a terminal symbol, but the file part is a nonterminal symbol.

The first component of BNF notation is a way to distinguish terminal symbols from nonterminal symbols. In submit_cse305 file I have used different fonts, this font for terminal symbols, and this font for nonterminal symbols. The text uses roman or bold font for terminal symbols, and <roman font inside angle brackets> for nonterminal symbols. That is also very common. When you read a BNF grammar someone else has written, there should be a mention of the system they use, but it should be pretty obvious also.

Consider a small programming language that has two kinds of statements: an assignment statement; and an if statement. We want to say

• A statement can be an assignment statement or an if statement.
• An assignment statement can be <variable> = <expression>
• An if statement can be if (<expression>) <statement>

Notice that the <statement> part is a nonterminal---it could be either of the kinds of statements.

The way BNF specifies how a nonterminal can be replaced is by a rule, with a left-hand side (LHS) which is always a nonterminal, and a right-hand side (RHS), which is a sequence of terminals or nonterminals, separated by a rewrite symbol. The text uses -> as a rewrite symbol; the symbol ::= is also often used. So we can rewrite and complete the specification of the statements of this small language as:

<statement> ->  <assignment>
<statement> -> <if>
<assignment> -> <variable> = <expression>
<if> -> if (<expression>) <statement>
<expression> -> <variable>
<expression> -> <variable> + <variable>
<expression> -> <variable> - <variable>
<variable> -> x
<variable> -> y
<variable> -> z

To use this grammar to generate a statement of this language, we start with <statement>, and derive a statement by steps. In each step, we choose a nonterminal of the string and replace it by the RHS of any rule in which that nonterminal is the LHS. For example,

<statement>
<if>
if (<expression>) <statement>
if (<variable>) <statement>
if (y) <statement>
if (y) <if>
if (y) if (<expression>) <statement>
if (y) if (<variable>) <statement>
if (y) if (z) <statement>
if (y) if (z) <assignment>
if (y) if (z) <variable> = <expression>
if (y) if (z) x = <expression>
if (y) if (z) x = <variable> + <variable>
if (y) if (z) x = y + <variable>
if (y) if (z) x = y + z

Notice that this grammar is recursive, <statement> derives a string in which <statement> occurs. Recursive grammars can generate infinitely long sentences.

This derivation can also be represented by a parse tree:
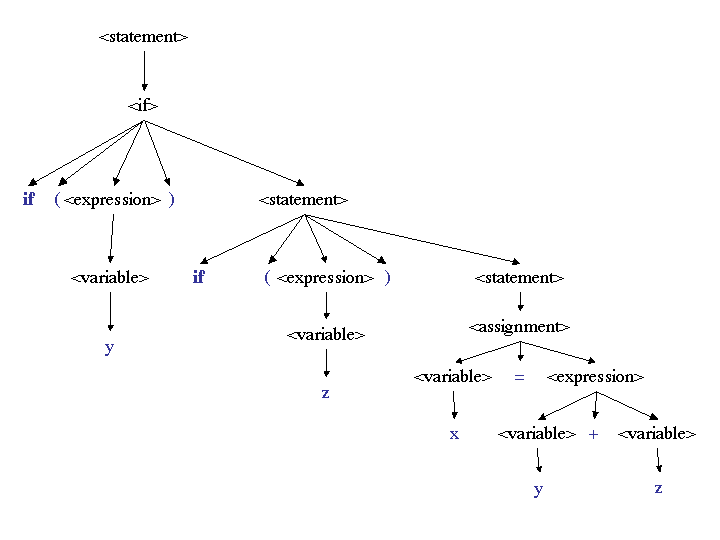
The sentence, itself, is formed by the leaves of the parse tree, read left to right. They are in blue for easier reading.

Notice that the tree makes the structure of the constituents of the sentence clear. It shows that y + z is an expression that forms the right-hand side of the assignment statement, and that if (z) x = y + z is the statement that is under the control of the if (y) condition.

When multiple rules of a grammar have the same LHS, they may be combined by connecting their RHSs with the or symbol, |. The grammar above becomes

<statement> ->  <assignment> | <if>

<assignment> -> <variable> = <expression>

<if> -> if (<expression>) <statement>

<expression> -> <variable>

              | <variable> + <variable>

              | <variable> - <variable>

<variable> -> x | y | z

A grammar may be ambiguous. Consider this grammar for expressions:

<expression> -> <variable>

              | <expression> * <expression>

              | <expression> + <expression>

<variable> -> x | y | z

The expression x * y + z has two derivations, as shown by these two parse trees:
The one on the left clearly indicates that the + is to be done before the *, while the one on the right clearly indicates that the * is to be done before the +.

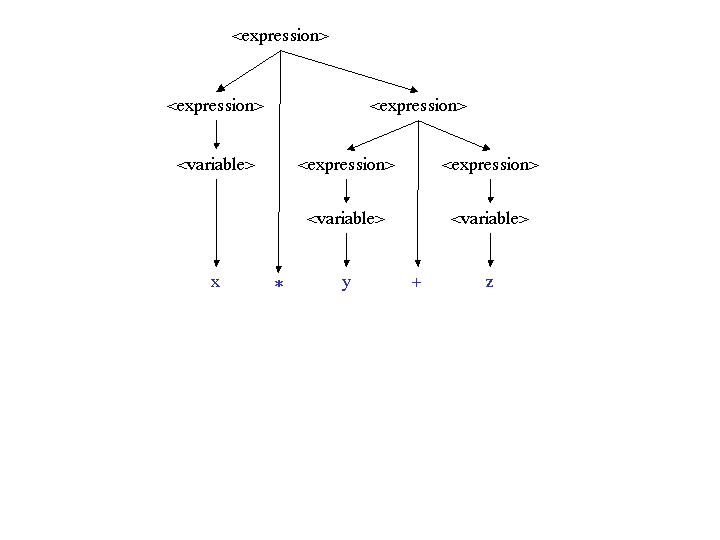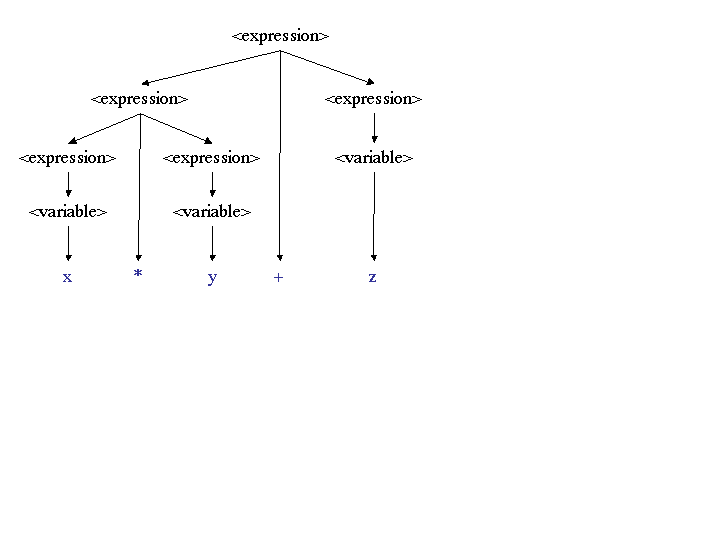The grammar can be made unambiguous by some small rewriting. We could have two versions:

1. 
   <expression> -> <variable>
   
                 | <variable> * <expression>
   
                 | <variable> + <expression>
   
   <variable> -> x | y | z
   

2. <expression> -> <variable>
   
                 | <expression> * <variable>
   
                 | <expression> + <variable>
   
   <variable> -> x | y | z
   

Using grammar 1, which is right recursive, the expression x * y + z only has the parse tree:

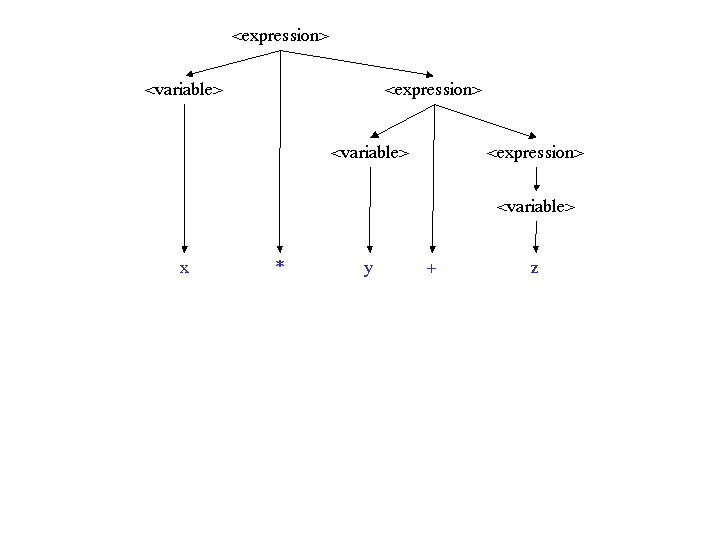
Using grammar 2, which is left recursive, the expression x * y + z only has the parse tree:

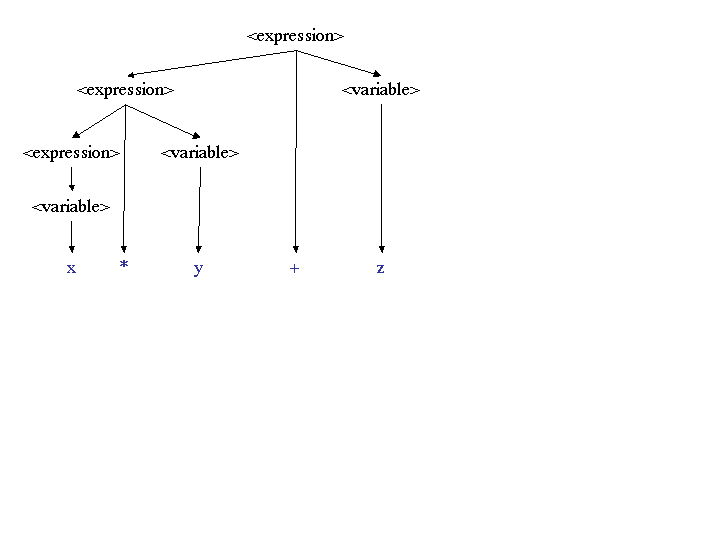
Notice that the left recursive grammar gives a left associative expression, while a right recursive grammar gives a right associative expression.

Of course, we really want * to always have higher precedence than +. For a grammar that does that, see Example 3.5 on page 133 of the text. Within a single precedence level, we usually want a left associative expression, and, therefore a left associative grammar. This, and the right associativity of **, is also illustrated by the BNF grammar in Example 3.5 (though not the EBNF version).

Sometimes, the grammar bottoms out at some nonterminals which are described, not in BNF, but in informal text. For example,

<variable> -> <identifier>

An <identifier> is a string of characters, the first of which can be an upper- or lower-case alphabetic character, and the rest of which can be upper- or lower-case alphabetic characters, decimal digits, or the _ character.

Extended Backus-Naur Form (EBNF)

EBNF adds several extensions to BNF, for an even more concise notation:

1. Some bracket notation, usually [], to indicate an optional part of the RHS. For example,

   <if> -> if (<expression>) <statement> [else <statement>]
   

2. Some kind of repetitive construct. For example enclosing a part of the RHS in curly brackets, {}, to indicate a sequence of 0 or more occurrences of the subsequence. For example,

   <decl> -> <type> <variable> {, <variable>};
   

   Sometimes, instead, the the section of RHS is enclosed in parentheses (if more than one symbol), and followed by a Kleene *, indicating 0 or more occurrences, or a Kleene +, indicating 1 or more occurrence. For example,

   <decl> -> <type> <variable> (, <variable>)*;
   

   
   or even, combining the optional notation with the repetitive notation,

   <decl> -> <type> <variable> [, <variable>]+;
   

   Notice, however, this does not distinguish left vs. right associativity.

3. If two RHSs are the same except for one constitutent, EBNF allows that constituent to be shown in parentheses with an infix | operator. For example,

   <expression> -> <variable>
   
                 | <expression> (* | +) <variable>
   
   <variable> -> x | y | z
   

4. A numeric superscript can be added to the closing bracket to indicate the maximum number of repetitions allowed, for example

   <variable> -> <letter> {<letter> | <digit>}5
   

   indicates that a variable name can have a mixture of letters and digits, as long as it starts with a letter, and is at most 6 characters long.

If any punctuation is allowed both in the metalanguage and in the object language, they must be distinguished. Often the object language symbols (terminal symbols) are underlined, surrounded by quotes, or put in bold font. For example,

<if> -> if (<expression>) <statement> [else <statement>]

For a nice example of the use of EBNF to define lexemes, see Haskell 98 Language and Libraries The Revised Report, Chap. 2, December 2002.

Last modified: Thu Feb 11 20:07:17 EST 2010
Stuart C. Shapiro <shapiro@cse.buffalo.edu>