Homework 6
Due by 8:00pm, Tuesday, April 15, 2025.
Make sure you follow all the homework policies.
All submissions should be done via Autolab.
Question 1 (Exponentiation) [50 points]
The Problem
We will consider the problem of exponentiating an integer to another. In particular, for non-negative integers $a$ and $n$, define Power$(a,n)$ be the number $a^n$. (For this problem assume that you can multiply two integers
in $O(1)$ time.) Here are the two parts of the problem:
- Part (a): Present a naive algorithm that given non-negative integers $a$ and $n$ computes
Power$(a,n)$ in time $O(n)$.Note
For this part, there is no need to prove correctness of the naive algorithm but you do need a runtime analysis.
- Part (b):
Present a divide and conquer algorithm that given non-negative integers $a$ and $n$ computes
Power$(a,n)$ in $O(\log{n})$ time.Important Note
To get credit you must present a recursive divide and conquer algorithm and then analyze its running time by solving a recurrence relation. If you present an algorithm that is not a divide and conquer algorithm you will get a level 0 on this entire part.
Hint
The following mathematical identity could be useful-- for any real numbers $b,c$ and $d$: $b^{c+d}=b^c\cdot b^d$.
Common Mistake
Be careful and make sure that you use the correct recursive calls. Many students end up with an $\Omega(n)$ time algorithm for the second part by not using the correct set of recursive calls.
Submission
Submit part (a) and (b) separately
You need to submit two (2) PDF files to Autolab: one for part (a) and one for part (b). While you can assume part (a) as a given for part (b), to get credit for part (a) you have to submit you solution for part (a) separately from part (b).
Make sure you submit the correct PDF to the correct submission link on Autolab. If you do not (e.g. if you submit Q1(a) PDF to Q2(a) or even Q1(b)), then you will lose ALL points.
We recommend that you typeset your solution but we will accept scans of handwritten solution-- you have to make sure that the scan is legible.
PDF only please
If Autolab cannot display your file, (irrespective of the reason) then you will get a zero (0) on the entire question.
Autolab might not be able to display files in formats other than PDF (e.g. Word cannot be displayed). Note that Autolab will "accept" your submission even if you submit non-PDF file, so it is YOUR responsibility to make sure you submit in the correct format.
Also the file size has to be at most 3MB.
Grading Guidelines
We will follow the usual grading guidelines for non-programming questions. Here is a high level grading rubric specific to part (a) of this problem:
- Algorithm details:
8points. Nothing else is needed. - Runtime Analysis:
2points.
- Algorithm idea:
10points. - Algorithm details:
10points. - Proof of correctness idea:
10points. - Runtime analysis:
10point. Note:If the algorithm is not a recursive divide and conquer algorithm or the run time analysis does not go through the recurrence time bounds, then you get level 0 for the entire part (b).
Note
The grading rubric above is somewhat non-standard. So please make sure you pay attention.
Note
If you do not have labeled and separated out algorithms details and runtime analysis for part (a) and proof idea, algorithm idea, algorithm details and runtime analysis for part (b), you will get a zero(0) in the corresponding parts irrespective of the technical correctness of your solution.
Note
Your must explicitly list your sources and collaborators when you upload your submission to Autolab. Note that there are only five allowed sources. If you have used a source that is not allowed, please do not submit your homework. If you did not consult any source or did not collaborate with anyone just say None.
Question 2 (Even Faster Integer Multiplication) [25 points]
The Problem
In this problem you will explore what happens if in the integer multiplication algorithm we saw in class we do the splitting of the numbers differently. But before we get to the final problem, let's start off with this one:
- Part (a): Define the recurrence relation \[ T(n)\le \begin{cases} c &\text{ if }n<3\\ 5T\left(\frac{n}{3}\right)+cn&\text{ otherwise}. \end{cases} \] Argue that $T(n)$ is $O\left(n^{\log_3{5}}\right)$.
We now come to the actual algorithmic problem:
- Part (b): Either by modifying the algorithm we saw in class or otherwise, present an algorithm that can multiply two $n$ bit numbers $a=(a_{n-1},\dots,a_0)$ and $b=(b_{n-1},\dots,b_0)$ in time $O\left(n^{\log_3{5}}\right)$, which is $O(n^{1.47})$ (and is better than the runtime of the algorithm we saw in class).
Hint
It might be useful to divide up the numbers into three parts each with roughly $n/3$ bits and then argue that one only needs to perform $5$ smaller multiplications of $n/3$-bit numbers instead of the trivial $9$ such multiplications. Further this support page might also be useful in generalizing the $O(n^{\log_2{3}})$ algorithm to one with a better runtime as required by this problem.)
Submission
Submit part (a) and (b) separately
You need to submit two (2) PDF files to Autolab: one for part (a) and one for part (b). While you can assume part (a) as a given for part (b), to get credit for part (a) you have to submit you solution for part (a) separately from part (b).
Make sure you submit the correct PDF to the correct submission link on Autolab. If you do not (e.g. if you submit Q1(a) PDF to Q2(a) or even Q1(b)), then you will lose ALL points.
We recommend that you typeset your solution but we will accept scans of handwritten solution-- you have to make sure that the scan is legible.
PDF only please
If Autolab cannot display your file, (irrespective of the reason) then you will get a zero (0) on the entire question.
Autolab might not be able to display files in formats other than PDF (e.g. Word cannot be displayed). Note that Autolab will "accept" your submission even if you submit non-PDF file, so it is YOUR responsibility to make sure you submit in the correct format.
Also the file size has to be at most 3MB.
Grading Guidelines
We will follow the usual grading guidelines for non-programming questions. Here is a high level grading rubric specific to part (a) of this problem:
- Proof idea:
10points.
- Algorithm idea:
3points. - Algorithm details:
3points. - Proof of correctness idea:
5points. - Proof details:
3points. - Runtime analysis:
1point. NOTE:If your algorithm runs in $\Omega\left(n^{\log_2{3}}\right)$ time, then you will get level 0 on all parts.
Note
If you do not have labeled and separated out and proof idea, algorithm idea, proof details, algorithm details and runtime analysis for part (b), you will get a zero(0) irrespective of the technical correctness of your solution for the corresponding part.
Note
Your must explicitly list your sources and collaborators when you upload your submission to Autolab. Note that there are only five allowed sources. If you have used a source that is not allowed, please do not submit your homework. If you did not consult any source or did not collaborate with anyone just say None.
Question 3 (Programming Assignment) [25 points]
Note
This assignment can be solved in either Java, Python or C++ (you should pick the language you are most comfortable with). Please make sure to look at the supporting documentation and files for the language of your choosing.
The Problem
In this problem, we will explore minimum spanning trees.
We are given an undirected, connected graph represented by its adjacency matrix representation. Our goal it to find a minimum spanning tree of that graph.
Input
The input file is given as an $n\times n$ matrix where each entry $(u,v)$ represents the weight of the edge between nodes $u\in \{0,1,\dots,n-1\}$ and $v\in\{0,1,\dots,n-1\}$. If there is no edge then the weight is -1. Edge weights will be 0 <= w <= 50.
w0,0 w0,1 w0,2 w0,3 ... w0,n-1
w1,0 w1,1 w1,2 w1,3 ... w1,n-1
.
.
.
wn-1,0 wn-1,1 wn-1,2 wn-1,3 ... wn-1,n-1
Output
The output is a list where every index corresponds to the node ID and the value in the index is the parent of the node. In other words, you need to output a rooted form of an MST (you can root the MST at any node).
[p0 p1 p2 .... pn-1] <- Where the subscript is the node ID and p is the parent node
Note
The root of the minimum spanning tree should have a -1 as its parent's node ID.
Note
There are more than one possible MST for a given input instance so your output might not match the sample output.
Example
Input:
Here's an example input of the following graph
-1 3 -1 2 -1 -1 -1 -1 4
3 -1 -1 -1 -1 -1 -1 4 -1
-1 -1 -1 6 -1 1 -1 2 -1
2 -1 6 -1 1 -1 -1 -1 -1
-1 -1 -1 1 -1 -1 -1 -1 8
-1 -1 1 -1 -1 -1 8 -1 -1
-1 -1 -1 -1 -1 8 -1 -1 -1
-1 4 2 -1 -1 -1 -1 -1 -1
4 -1 -1 -1 8 -1 -1 -1 -1
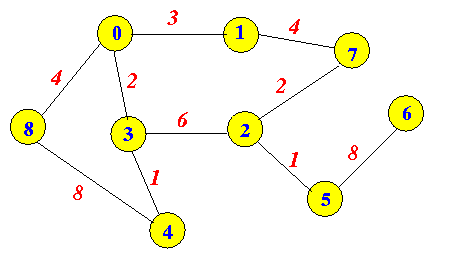
Output for the above example:
Where node 0 is the root node.
[-1, 0, 7, 0, 3, 2, 5, 1, 0]
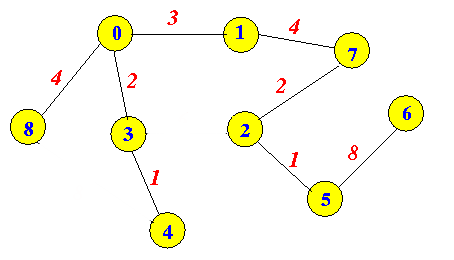
Hint
One can implement Prim's algorithm (which we saw in class for the adjacency list format) in time $O(n^2)$ where $n$ in the total number of nodes. It can be argued that this is optimal.
Design an algorithm that works on the adjacency matrix format itself. If e.g. you try to convert it into adjacency list format and then apply the algorithm we have seen in class (which works on adjacency list format), you might not pass all testcases.
Note
Both the input and output parsers in each of the three languages are already written for you. Note that you have to work with the input data structures provided (which will come pre-loaded with the data from an input file).
Addition is the only change you should make
Irrespective of what language you use, you will have to submit just one file. That file will come pre-populated with some stuff in it. You should not change any of those things because if you do you might break what the grader expects and end up with a zero on the question. You should of course add stuff to it (including helper functions and data structures as you see fit).
Directory Structure
├── src
│ └── ub
│ └── cse
│ └── algo
│ ├── Driver.java
│ └── Solution.java
├── testcases/
│ ├── input1.txt
│ ├── input2.txt
│ ├── input5.txt
├── outputs/
│ ├── output1.txt
│ ├── output2.txt
│ └── output5.txt
You are given two coding files: Driver.java and Solution.java. Driver.java takes the input file, parses it and creates an instance of the class and prints result that is output by your code. You only need to update the Solution.java file. You may write your own helper methods and data structures in it.
The testcases folder has 3 input files and their corresponding output files for your reference. We will use these three input files (and seven others) in our autograding.
Method you need to write:
/**
* You will fill this out.
* We expect you to find out the minimum spanning tree. You may choose your root arbitrarily.
* The int[] contained will represent this tree. Each value will be the parent of the node with the index value.
* For example, if output[7] = 12, then node 7 has 12 as its parent. For the root node, it should have a value of
* -1.
* @return a representation of the MST.
*/
public int[] outputEdges() {
return null;
}
The Solution class has 1 instance variables:
adj_matrixwhich is aArrayList<ArrayList<Integer>>, which is a 2D list which represents the Adjacency Matrix of the input graph.
int [] array whose indices represent node ids and whose values represent the parent node of the index node (the root of the MST should have a parent of $-1$).
Compiling and executing from command line:
Assuming you're in the same directory level as Driver.java. Run javac src/ub/cse/algo/*.java to compile.
To execute your code on input1.txt, run java -cp "src" ub.cse.algo.Driver testcases/input1.txt. The output array will be printed to stdout.
Submission
You only need to submit Solution.java to Autolab.
Directory Structure
├── Driver.py
├── Solution.py
├── testcases/
│ ├── input1.txt
│ ├── input2.txt
│ ├── input5.txt
├── outputs/
│ ├── output1.txt
│ ├── output2.txt
│ └── output5.txt
You are given two coding files: Driver.pyand Solution.py. Driver.py takes the input file, parses it and calls your output_Edges() method on data structures it creates. It then prints the parent of each node in the computed spanning tree. You only need to update the Solution.py file. You may write your own helper methods and data structures in it.
The testcases folder has 3 input files and their corresponding output files for your reference. We will use these three input files (and seven others) in our autograding.
Method you need to write:
def output_edges(self):
################# YOUR CODE GOES HERE ##################
return [] # Return empty list for now
The Solution method is called with 1 argument
graphwhich is a 2D list which represents the Adjacency Matrix of the input graph
Your method is expected to return a list whose indices represent node ids and whose values represent the parent node of the index node (the parent of the root of the MST should be $-1$).
Executing from command line:
Assuming you're in the same directory level as Driver.py and you want to run your code on the input1.txt. Run python Driver.py testcases/input1.txt.
Submission
You only need to submit Solution.py to Autolab.
Directory Structure
├── Driver.cpp
├── Solution.cpp
├── testcases/
│ ├── input1.txt
│ ├── input2.txt
│ ├── input5.txt
├── outputs/
│ ├── output1.txt
│ ├── output2.txt
│ └── output5.txt
You are given two coding files: Driver.cpp and Solution.cpp. Solution.cpp takes the input file, parses it and creates an instance of the class Solution and calls the outputEdges() method on it. It then prints the parent of each node in the computed spanning tree. You only need to update the Solution.cpp file. You may write your own helper methods and data structures in it.
The testcases folder has 3 input files and their corresponding output files for your reference. We will use these three input files (and seven others) in our autograding.
Method you need to write:
vector<int> Solution::outputEdges() {
/*
* Output the edges of the MST.
*/
return output;
}
Note: The output for this function must output a vector of int
The Solution class has 1 member variable.
graphWhich is a 2D vector that represents the Adjacency Matrix of the input
Compiling and executing from command line:
Assuming you're in the same directory level as Solution.cpp. Run g++ -std=c++11 Driver.cpp to compile.
To execute your code on input1.txt, run ./a.out testcases/input1.txt.
Submission
You only need to submit Solution.cpp to Autolab.
Grading Guidelines
We will follow the usual grading guidelines for programming questions.
For those of you who are feeling a little ambitious
For the top 3 submissions in the scoreboard in Java, the top 2 submissions in the scoreboard in Python and the top 1 submissions in the scoreboard in C++, we are offering 2.5 bonus points. But be warned! You should not be spending too much time on this. We rather you work on Questions 1 and 2 above.