Recitation 5
Recitation notes for the week of Feb 19, 2025.
Homework 3, Question 1
A seating
A seating (as you might expect) is an assignment of the $p$ ADFs to the $p^2$ chairs in the theater so that each ADF gets his/her own chair.
Only 1 ADF will be in the first row, but having $p^2$ seats means that there is enough space in each row to hold all ADFs, and there are enough rows that each ADF could have their own row. All ADF's should be connected to a friend in the 1st row via the distance compatibility property.
Admissible seating
A seating is called admissible if
- for every pair of friends $(b_1,b_2)$, they can
talkto each other during the movies
They sit 1 or 0 rows apart - some ADF is assigned a seat in the first row
Self explanatory, someone sits in the front row - the seating satisfies the
distance compatibleproperty.
Each ADF is friendship distance from the ADF in the front row. If they are direct friends of the front row ADF, they sit in the second row. If they are friends of friends, they sit in the third row and so on.
Example 1
An example seatings with explanation of why they uphold the properties:
Friendships = { (A, B), (B, C) }
+--+---+--+
| | A | |
+--+---+--+
| | B | |
+--+---+--+
| | C | |
+--+---+--+
+---+---+---+
| | B | |
+---+---+---+
| A | | C |
+---+---+---+
| | | |
+---+---+---+
These are both valid seatings for the ADFs.
How the first example upholds the properties
- A can talk with B, B can talk with C. All friends can talk to each other since they are at most 1 row apart.
- ADF A is seated in the first row
- A is first level friends with B, because they are directly friends. A is second level friends with C because A is friends with B who is friends with C. Thus, the distance compatible property is upheld because B is 1 row from A and C is 2 rows away.
How the second example upholds the properties
- B can talk with A, and B can talk with C. All friends can talk to each other.
- ADF B is seated in the first row.
- A and C are both direct friends of B, and they are 1 row.
But why are A and C not far apart?
Note that A and C have friendship distance of $2$ but they are sitting in the same row. However, this does not violate the
distance compatibilityproperty since neither A nor C are in the first row.
Example 2
Friendships = { (A,D),(C,B),(A,C),(B,E) }
+---+---+---+--+--+
| | A | | | |
+---+---+---+--+--+
| C | | D | | |
+---+---+---+--+--+
| | B | | | |
+---+---+---+--+--+
| | E | | | |
+---+---+---+--+--+
+---+---+---+--+--+
| | C | | | |
+---+---+---+--+--+
| A | | B | | |
+---+---+---+--+--+
| | D | E | | |
+---+---+---+--+--+
These are both valid seatings for the ADFs.
Note: Not all seats are shown, but there are 5x5 seats available.
How the first example upholds the properties
- A is friends with C and D, and can talk to both of them. C is friends with B, they can talk together. B is friends with E and they can talk together.
- ADF A is seated in the first row
- A is direct friends with C and D, and they are correctly 1 row behind A. C is friends with B, which makes B two levels away from A so the third row is a correct placement. B is friends with E, which makes E three levels away from A so the fourth row is a correct placement.
How the second example upholds the properties
- C is friends with A and B, and they can talk since they are 1 row apart or in the same row. A is friends with D, and they are 1 row apart. B is friends with E and they are 1 row apart. All friends can talk.
- ADF C is seated in the first row
- C is friends with both A and B, and they are 1 row behind C, which is the correct friendship distance. A is friends with D, which makes D two rows away from C which is correct. B is friends with E, which makes two rows away from C the correct placement for E.
Q1 Part (a)
The Problem
For part (a) you must formally define the problem in terms of properties of a graph
Formalizing the problem
- How to represent the Ava DuVernay fans (ADFs) as a graph $G = (V, E)$?
- Fans are the vertices of the graph $G$
- If ADFs $i$ and $k$ are friends, then $(i, k)$ exists in the set of edges $E$
- How to define a seating?
- A seating is a one-to-one function $s:V\to [p]^2$, i.e. if $s(u)=(r,c)$, then it means that $u$ is seated in row $r$ and column $c$, for notational simplicity the rows and columns are indexed by $[p]$.
- Defining an
admissible seatingin terms of properties of a graph $G$:- If there exists an edge (friendship) between ADFs $i$ and $k$, then the absolute value of the difference between their assigned rows must be less than or equal to $1$, i.e. if $s(i)=(r_i,c_i)$ and $s(k)=(r_k,c_k)$, then $|r_i-r_k|\le 1$.
This means that connected nodes must be placed 1 or 0 rows apart - Some node (ADF) is placed in the first row, i.e. there exists some ADF $u\in V$ and $c\in [p]$ such that $s(u)=(1,c)$.
This implies that you should start by seating a single ADF - This third property, the
distance compatibleproperty, must be solved on your own for part (a).
- If there exists an edge (friendship) between ADFs $i$ and $k$, then the absolute value of the difference between their assigned rows must be less than or equal to $1$, i.e. if $s(i)=(r_i,c_i)$ and $s(k)=(r_k,c_k)$, then $|r_i-r_k|\le 1$.
Q1 Part (b)
For part (b) you should use the graph from part (a) to come up with an algorithm that will efficiently (i.e. in time polynomials in $p$ and $f=|E|$) seat the ADFs in an admissible seating.
There might be a reduction to a problem that you have seen in class.
Homework 3, Question 2
We first recall the question:
The Problem
A triangle in a graph $G=(V,E)$ is a $3$-cycle; i.e. a set of three vertices $\{u,v,w\}$
such that $(u,v),(v,w),(u,w)\in E$. (Note that $G$ is undirected.) In this problem you will design
a series of algorithms that given a connected graph $G$ as input, lists all
the triangles in $G$. (It is fine to list one triangle more than once.) We call this the triangle listing problem
(duh!). You can assume that as input you are given $G$ in both the adjacency matrix and
adjacency list format. For this problem you can also assume that $G$ is connected.
Sample Input/Output pair
- Input: Consider the following input $G$ (note that this is a bit different from the example in the HW 3 Q3 problem statement)
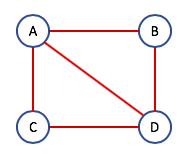
- Output: The list $[\{A,B,D\}, \{A,C,D\}]$.
Question 2, part (a)
The Problem
Present an $O(n^3)$ time algorithm to solve the triangle listing problem.
Algorithm Idea
Let us assume we have access to a function Check-if-triang that takes as input $G=(V,E)$ and three vertices $u,v,w\in V$ and outputs true if $\{u,v,w\}$ is a triangle in $G$ and false otherwise.
Then the algorithm is simple: just go through all possible $n^3$ triples $\{u,v,w\}$ and if Check-if-triang$(G,u,v,w)$ outputs true then we add $\{u,v,w\}$ to the output.
Duplicates
The above algorithm would output the same set $\{u,v,w\}$ six times but that is OK for this problem. As long as you (1) only output triangles; (2) output all triangles and (3) maintain the given time bound, you can have duplicates.
Exercise
Show that Check-if-triang can be implemented in $O(1)$ time.
Algorithm Details
Even though this is not needed for your HW submission, we write down the details of the $O(n^3)$ time algorithm (assuming Check-if-triang as a blackbox of course):
Let GL and GM be the adjacency list and adjacency matrix representation of G (both are input).
# GL is an array of pointers to linked list. The indices to vertices are in GL.keys()
#Get the set of vertices
V = GL.keys()
L = null
#Cycle through all triples
for u in V:
for v in V:
for w in V:
if Check-if-triang(GM,u,v,w) == true:
Add {u,v,w} to L
return L
Question 2, part (b)
The Problem
This has two sub-parts:
- Let $\Delta$ denote the maximum degree, i.e. \[\Delta=\max_u n_u.\] Present an $O(n\cdot\min(m,\Delta^2))$
time algorithm to solve the triangle listing problem.
Hint
It might be useful to consider all the potential triangles that have one fixed vertex $u\in V$ as one of its vertices.
- Present an $O(m^{3/2})$ algorithm to solve the triangle listing problem.
Two Comments
We conclude with two comments:
- The algorithm from part (a) is correct but it not enough for part (b) since it runs too slowly.
- For first sub-part (i.e. the runtime $O(n\cdot\min(m,\Delta^2))$), it is possible to solve that sub-part by looking at the triply nested loop in the algorithm for part (a) and then to figure out how to reduce the number of iterations. (Also look at the hint above.)
Homework 3, Question 3
One property of BFS that is useful for Q3 on HW 3:
BFS and distance
Say we run BFS from node $s$ in graph $G=(V,E)$ and let the layers be denoted by $L_0,L_1,\dots$. If $u\in L_i$ for any $u\in V$ and $i\ge 0$, then we have that the distance between $s$ and $u$ is exactly $i$. This is (3.3) in the textbook.
Please see the textbook for a proof of this claim.
Further Reading
- Make sure you carefully read the policy documents: Syllabus and Homework policies.