Recitation 9

Recitation notes for the week of March 26, 2025.

HW 5, Question 1

The HW 5 webpage has the detailed description of the problem: here we just give a summary:

Overview of the problem

We want to compute the intersection of $n$ sets in a distributed manner. We are given a graph $G=(V,E)$, where each node $u\in V$ gets a set $S_u\subseteq [M]$. In particular, the set is represented as a binary array $A_u$. There is a pre-designated special node $t$, which at the end of the protocol must compute the intersection of all the $n$ sets. In this problem, we do not care about the runtime but the total cost of communication (where sending one bit over an edge $e\in E$ incurs a cost of $c_e$).

We will talk about the problem in terms of examples.

Example 1

In this case $G$ is the following graph: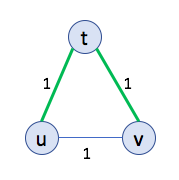

In the above graph an MST is shown with the green edges.

The input sets are defined as follows (note $n=3$ and $M=5$): \[S_u=\{1,2,5\},\] \[S_v=\{2,4\},\] \[S_t=\{2,3,5\}.\] The corresponding array representation will be \[A_u =[1,1,0,0,1],\] \[A_v =[0,1,0,1,0],\] \[A_t =[0,1,1,0,1],\]

Note that at the end, $t$ needs to know \[\{1,2,5\} \cap \{2,4\} \cap \{2,3,5\} =\{2\}\] or equivalently, \[B~~ =[0,1,0,0,0].\]

Here is a simple protocol: $u$ and $v$ send their input $A_u$ and $A_v$ to the node $t$ (on the edges $(u,t)$ and $(v,t)$) respectively. At that point $t$ has all the three sets and can compute the output $B$ without any further communication.

Note

Communication cost of the above protocol is $1\cdot 5 +1\cdot 5 =2\cdot 5=10$.

Example 2

In this case $G$ is the following graph: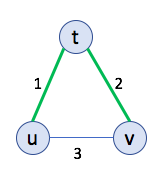

In the above graph an MST is shown with the green edges.

Consider the case when all the input sets are exactly the same as in Example 1. Thus, node $t$ needs to output $\{2\}$ (or equivalently $[0,1,0,0,0]$ as before). Further, the same protocol outlined in Example 1 works as is in this case.

Note

Communication cost of the protocol from Example 1 is now $1\cdot 5 +2\cdot 5 =3\cdot 5=15$.

Example 3

In this case $G$ is the following graph: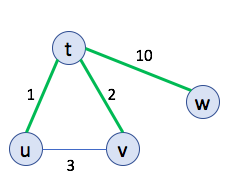

In the above graph an MST is shown with the green edges.

Consider the case when all the input sets $S_t,S_u,S_v$ are exactly the same as in Example 1. But we have another set now \[S_w=\{3,4,5\} \text{ or equivalently } A_w=[0,0,1,1,1].\] Thus, node $t$ needs to output $\emptyset$ (or equivalently $[0,0,0,0,0]$).

Here is the natural generalization of protocol for Example 1 for this case. As in the protocol for Example 1, $u$ and $v$ send their inputs to $t$. Now, in addition $w$ sends its input $A_w$ to $t$ via the edge $(w,t)$.

Note

Communication cost of the above protocol is $1\cdot 5 +2\cdot 5 +10\cdot 5 =13\cdot 5=65$.

Some important clarifications on what the algorithm can do and cannot do

Part (a)

We start by recalling the problem statement of part (a):

The problem

You will argue part (b) for two special cases of $G$:

  1. Show that when $G$ is a complete graph on $n$ vertices (i.e. $G=([n],E)$ where $E=\{(i,j)|i<j\in [n]\}$) and $c_e=1$ for every $e\in E$, there is a protocol whose worst-case communication cost over all inputs over the universe $[M]$ is $O(n\cdot M)$.
  2. Show that when $G$ is a star graph on $n$ vertices with $t$ as its center (i.e. $G=([n],E)$ where $E=\{(t,j)|j\neq t\in [n]\}$) and $c_e=1$ for every $e\in E$, there is a protocol whose worst-case communication cost over all inputs over the universe $[M]$ is $O(n\cdot M)$.

Note

We would like to point out two things:

  1. Since for both the complete graph and star graph above, we have $MST(G)=n-1$, the bound of $O(n\cdot M)$ in both sub-parts is indeed $O(MST(G)\cdot M)$ for the special case of $G$.
  2. Note that your protocols for part (a) above can use the special structure of the complete graph while your algorithm for part (b) should work for any network topology $G$.

Algorithm Idea Part 1

Every $u\in V\setminus\{t\}$ sends all of its $A_u$ to t via the edge $(u,t)$. Then t computes the final output (since it has $Au$ for every $u∈V$). Note that when this is specialized to $n=3$, this algorithm/protocol reduces to the ones stated in Example 1. Note that $t$ has $A_u$ and $A_v$ from from the nodes $u$ and $v$ and then all $t$ has to do is loop every entry in $A_u, A_v$ and $A_t$ to construct the required output $B$.

Algorithm Detail Part 1

Even though this is not needed for your HW submission, we write down the details, so that it helpful for part (b).

                                    //This code is run at each node u in V

                                    if u!= t:
                                        Send Au to t via the edge (u,t)
                                        return #At this point this node does not do anything else and basically terminates
                                    else: # The rest of the code is just for t

                                        B = At

                                        while t has not received an array from all u!=t:
                                            t receives array C from u #This is triggered when node t receives C=Au from u

                                            for i = 1 to M:
                                                B[i] = B[i] and C[i]

                                        #At this point has received arrays from all other nodes u
                                        return B #This is the final output

Bounding Communication cost

The only communication happens in line 4 of the algorithm above. Further, this communication leads to sending $M$ bits from every vertex $u\neq t$ to $t$, incurs cost $1\cdot M=M$ (this is where we use the fact that $c_e=1$ for every $e$). Since there are $n-1$ vertices $u\neq t$, we have that the overall communication cost of $(n-1)\cdot M$, which is $O(nM)$, as desired

Hint for part 2

The algorithm needed for part 2 (Star Case) is very similar to the algorithm used for part 1.

Part (b)

The problem you need to solve

Design an algorithm whose worst-case communication cost over all inputs over the universe $[M]$ is $O(MST(G)\cdot M)$, where $MST(G)$ is the cost of an MST on $G$ (i.e. it is the sum of costs of all edges in the MST). Note that the algorithm gets both $G$ (along with its edge costs) and the arrays $A_u$ for every $u\in V$ as input. Note that the algorithm is only provided $G$ as input-- if it needs to know something about the graph $G$, then it needs to compute it by itself. You should assume that $G$ is connected.

We do not have to add beyond what we said in part (a) except:

Some clarifications

Some clarifications on what the algorithm can and cannot do:

  • Your algorithm can use the knowledge of $G$ to build a protocol: i.e. the sequence of bits that should be exchanged over any edge (and when to send those bits) but it has to work for any connected $G$. Note that this means you can do whatever pre-processing you want on $G$: no restriction on time complexity.
  • Once the protocol is built, the rest of the computation happens in a distributed manner. In other words any point of time and any node $u$, what bit(s) $u$ sends over an edge $(u,v)\in E$ depends only on $A_u$ and all the bits that $u$ has received till this point of time. (Again what computation to apply to compute these bits to be sent over is determined by the protocol.)
  • At the end of the run of the protocol, the node $t$ has to output the final answer $B$ only based on $A_t$ and all the bits it has received from its neighbors over the entire run of the protocol.

HW 5, Question 2

The problem you need to solve

Consider the following problem. Given a Directed Acyclic Graph (or DAG) G with arbitrary weights on the edges (i.e. they can be positive or negative) with n vertices and m edges, and given two vertices s and t, compute the shortest path from s to t in G. (You can assume that G is given to you in the adjacency list format.).

Topological Ordering

Refer to the care package on topological ordering.

Part (a)

The problem you need to solve

Fix any topological ordering of $G$. Then consider the new graph $G′$ that one obtains by removing all vertices from $G$ that come before $s$ in the chosen topological ordering. (Note that when you remove a vertex, you also remove all of its incident edges.) Then argue that any $s−t$ path in $G$ is also an $s−t$ path in $G’$.

Proof Idea

Proof by Contradiction

Before we start our proof we must first fix a topological ordering of $G$ using the algorithm from the book. After the new ordering now we have $G’$. In the arguments below we will assume that this topological ordering has been fixed.

We begin with the following result (you need to finish this off on your own):

Lemma 1

Every node $u$ in any $s-t$ path comes after $s$ in the topological ordering.

Given Lemma 1 above, the rest of the argument is fairly straightforward. Fix any arbitrary $s-t$ path in $G$. Then by Lemma 1, since all nodes in this graph comes after $s$ in the topological ordering, all of these nodes are also present in $G'$. Further, any edge $(u,v)$ in the $s-t$ path is also present in $G'$ since both of $u$ and $v$ are still present (note that an edge is thrown away if and only if one of its end points are thrown away when computing $G'$ from $G$). This implies that the $s-t$ path still remains in $G'$, as desired.

Part (b)

The problem you need to solve

Present an $O(m+n)$ algorithm to compute the shortest path from $s$ to $t$ in $G$

Hint

Part (a) might be useful in solving (b).

Boruvka’s Algorithm

This is another algorithm to find the minimum spanning tree for a graph with distinct edge weights (none of the edges have the same value).

Algorithm Idea

The goal of the algorithm is to connect "components" using the shortest edge between components. It begins with all of the vertices considered as separate components and then continues till there is one connected component left (which can be proven is an MST).

Next we present the Algorithm Details, courtesy of Wikipedia .

Algorithm Details


                            //Input: A connected graph G whose edges have distinct weights

                            Initialize a forest T to be a set of one-vertex trees, one for each vertex of the graph.

                            while T has more than one component:
                                for each component C of T:
                                    Let S be an empty set of edges
                                    for each vertex v in C:
                                        Find the cheapest edge from v to a vertex outside of C, and add it to S
                                    Add the cheapest edge in S to T
                                Combine trees connected by edges to form bigger components

                            return T // The set of edges in T forms the MST of G

Note

An edge can be selected twice (by two different components). This is fine.

Example 4

We consider the run of the Algorithm on the following graph:

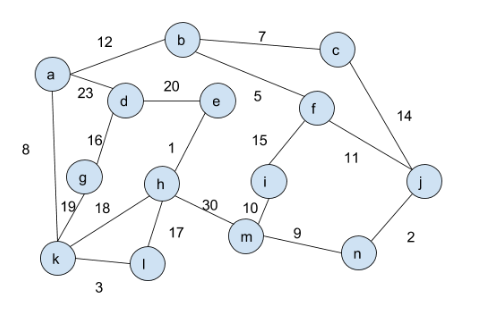
  1. Initially all the vertices themselves form their own component.
  2. In the first iteration of the while loop, all the red edges are picked and added to T:
    .
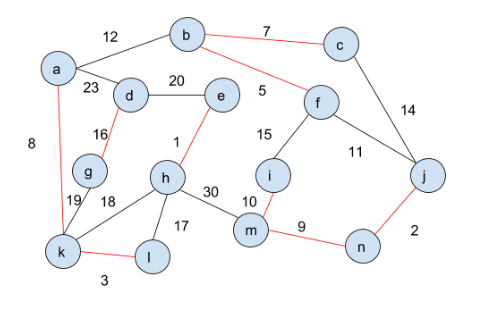  3. In the second iteration of the while loop, all the green edges are picked and added to T:
    .
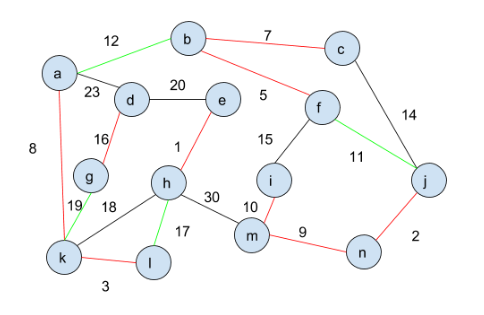  4. At this point, we are done.

There are two more examples on the Wikipedia page .

Complexity

Note that the while loop will halve the number of components each time. We start with $n$ components (the number of vertices), so the while loop runs at most $\log{n}$ times. In each iteration of the loop, we look through the edges, taking $O(m)$ time. Thus, overall we have $O(m \log{n} )$ time.

Correctness

Proof Idea

As in class we consider the case when all the edge costs are distinct. Then note that the algorithm in each iteration of the while loop, add the cheapest crossing edge for the cut $(C,V\setminus C)$ for every (non-empty) component $C$. Thus, by the cut property lemma, this is a "safe" choice.

After each addition of an edge, the algorithm creates a forest in the original graph. As, we just argued, this forest does not have any edges that would not be in all MSTs. Finally, the algorithm runs until there is only one component. A forest with one component is a tree.