Comparison

Two points are important here. First, type and function declarations now read real*8, which is one way of declaring double precision arithmetic; the other way is double precision. Furthermore, system-defined functions like sin, cos, abs absolute value are declared by double precision names, like dsin, dcos, dabs. The second point is the declaration of real numbers as, for example, 2.0d0. The ``d0'' fills out all remaining bits with zero. If you do not use the ``d0'', then it is possible for the latter bits to be contaminated with non-zero entries, and pollute subsequent calculations.

One other new structure is the common block. In the code, the value of is shared among the main program and the function subroutines. This avoids the need to redefine in each subroutine.

Some sample output from the code deriv.f follows:

EBP on einstein> deriv
At what point do you wish to evaluate                     the derivative?
0.0
KK   x          approx f'         exact f'               difference
  -1  0.    5.8778525229247    6.2831853071796   0.40533278425486
  -2  0.    6.2790519529313    6.2831853071796    4.1333542482498D-03
  -3  0.    6.2831439655590    6.2831853071796    4.1341620636182D-05
  -4  0.    6.2831848937626    6.2831853071796    4.1341701439990D-07
  -5  0.    6.2831853030454    6.2831853071796    4.1341703393982D-09
  -6  0.    6.2831853071382    6.2831853071796    4.1342040901782D-11
  -7  0.    6.2831853071792    6.2831853071796    4.1300296516056D-13
  -8  0.    6.2831853071796    6.2831853071796    4.4408920985006D-15
  -9  0.    6.2831853071796    6.2831853071796  0.
  -10  0.    6.2831853071796    6.2831853071796  0.
  -11  0.    6.2831853071796    6.2831853071796    8.8817841970013D-16
  -12  0.    6.2831853071796    6.2831853071796  0.
  -13  0.    6.2831853071796    6.2831853071796  0.
  -14  0.    6.2831853071796    6.2831853071796   -8.8817841970013D-16
  -15  0.    6.2831853071796    6.2831853071796  0.
  -16  0.    6.2831853071796    6.2831853071796  0.
EBP on einstein>

We see that somewhere around , the derivative is as good as it ever gets. In this example, the later approximations remain accurate. However consider

EBP on einstein> deriv
At what point do you wish to evaluate                     the derivative?
1.5707963
KK          x          approx f'         exact f'               difference
  -1    1.5707963   -4.4840499506386   -5.6717398582852   -1.1876899076466
  -2    1.5707963   -5.5830986537200   -5.6717398582852   -8.8641204565163D-02
  -3    1.5707963   -5.6632087651781   -5.6717398582852   -8.5310931070302D-03
  -4    1.5707963   -5.6708901048642   -5.6717398582852   -8.4975342099103D-04
  -5    1.5707963   -5.6716549164687   -5.6717398582852   -8.4941816420603D-05
  -6    1.5707963   -5.6717313633106   -5.6717398582852   -8.4949745220442D-06
  -7    1.5707963   -5.6717389957020   -5.6717398582852   -8.6258318354737D-07
  -8    1.5707963   -5.6717396846292   -5.6717398582852   -1.7365600424313D-07
  -9    1.5707963   -5.6717395528022   -5.6717398582852   -3.0548295892885D-07
  -10    1.5707960   -5.6717409405809   -5.6717398582852    1.0822957072776D-06
  -11    1.5707960   -5.6717070787814   -5.6717398582852   -3.2779503742475D-05
  -12    1.5707960   -5.6710701598579   -5.6717398582852   -6.6969842725761D-04
  -13    1.5707960   -5.6650000000000   -5.6717398582852   -6.7398582851617D-03
  -14    1.5707960   -5.6166666666667   -5.6717398582852   -5.5073191618495D-02
  -15    1.5707960   -5.8000000000000   -5.6717398582852   0.12826014171484
  -16    1.5707960    NaN               -5.6717398582852    NaN  
 Note: the following IEEE floating-point arithmetic exceptions 
 occurred and were never cleared; see ieee_flags(3M): 
 Inexact;  Invalid Operand; 
 Note: IEEE NaNs were written to ASCII strings or output files; see econvert(3). 
 Sun's implementation of IEEE arithmetic is discussed in 
 the Numerical Computation Guide.
EBP on einstein>

In this second example, evaluating the derivative near 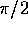, the numerical approximation actually got worse after the x-values were closer than about 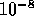! The reason for this degrading performance can be understood if you know a little about Taylor series. Recall that one can write

Solving this for 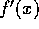, we find

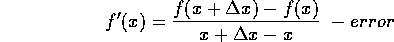
where the error term 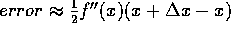. There is a second source of error, not explicitly written, due to inaccuracies in evaluating f. The best approximate derivitive, then, is when this sum of errors is minimized. In the calculations above, the optimum accuracy in approximating in double precision is about 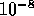; this is (about) the square root of the smallest number the machine can resolve (the machine epsilon). For most numerical derivatives, a typical 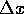to use is 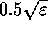, where is the machine epsilon (for the given precision).

One can get better accuracy in the derivative approximation by using a so-called centered difference:

We leave it to you to make the necessary modifications in the code to implement a centered difference formula.

Having taken this diversionary path into numerical differentiation, you are now in a position to incorporate a numerical approximation of into your Newton's method code.