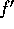The
second option available when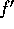 
is not easily evaluated
is to compute the derivative numerically. Recall the
formula from calculus for the derivative,
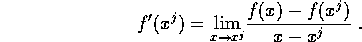
Well, we can approximate the derivative by taking x very close
to 
. How close is ``close enough''? Answering this question
draws us afield from solving nonlinear equations, but it is a
worthwhile diversion.
When we were learning about IEEE arithmetic, we saw that
a computer can only resolve the difference between two numbers
up to a certain point -- about 
in single precision.
FORTRAN supports double precision arithmetic, in which
each number is represented by twice as many bits as in single precision.
The smallest number recognized as different from zero in
double precision arithmetic is about 
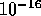. This limit on resolution
gives us a starting place for a study of numerical
differentiation.
In this study, it is perhaps better to see a specific
example with some numbers first, then
try to understand from whence these numbers came. For this example
we use functions for which we know the derivative. Here is a code
that computes the derivative of a function f numerically,
and compares it with 
.