Introduction The objective for the next several classes is to develop
tools for finding root(s) of a nonlinear equation. That is,
for finding x such that 
.
Simple algebra
gives us the root for a linear equation. For consider the
linear equation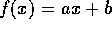 
. If a=0, then the line is
horizontal; unless b=0, there are no roots and if b=0,
the function is identically zero, and all x's are roots.
If 
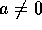, then setting 
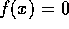yields
So, providing 
, for any b the root --the only root-- is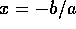 
.
Simple algebra also gives us the roots of a quadratic equation
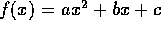. (This is really a quadratic only
if 
.) Recall the quadratic formula
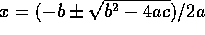Thus if the discriminant 
is positive, there
are two distinct real roots; if the discriminant is zero, there are
two roots, but they are equal; if the discriminant is negative,
there are no real roots. But the quadratic formula, useful though it is,
does not always give us information in the most useful form.
Consider, for example, the quadratic with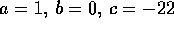 
; that is,
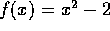. The quadratic formula tells us
.
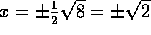This is the answer, but we do not have a feeling for exactly big
is (without plugging into our calculators).
So the programs we will construct need to provide us with
quantative information about the root we find.
There is a formula for roots of cubics and quartics. But in the
mid-nineteenth century, it was shown that there is no formula
for quintic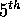s (
powers). That proof also showed that
there is no formula for an infinite number of higher odd powers.
And we have said nothing about finding roots of non-polynomial
functions.
So there is need for us to figure out good methods for determining roots. We will present three methods for root-finding: bisection, false position, and Newton's method. These methods are iterative. That is, given a guess of a root, or the interval in which the root lies, the method refines that guess several times, obtaining (hopefully) better and better guesses, until we are ``close enough'' to the true root.
Bruce Pitman