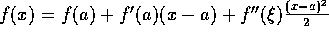It is appropriate to spend some time considering what sorts of
errors are present in an algorithm such as the two integration
methods. Error analysis is based on a Taylor expansion, with remainder.
For any point x, consider a nearby (fixed) point, a.
We can expand
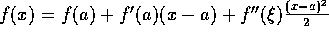, where
is some point between x and a.
For specificity, consider a subinterval with left endpoint a and
right endpoint b. To approxiamate the error in the subinterval,
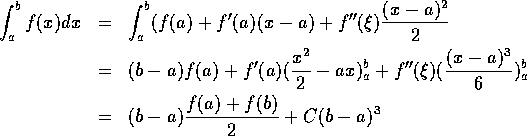
So in each subinterval, the trapezodial rule makes an error
(this is the local truncation error).
There are N such subintervals
so the net error in the integration is approximately
(global truncation error).
That is, the
trapezodial rule is second-order accurate.
Note: Using just a rectangle based on right or left endpoints,
the Taylor exapansion reads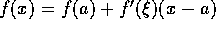 
. The
error then goes like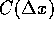 
, i.e. first-order accuracy.
Now look at your results from you trapezodial integration
assignment. For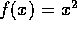 
, you cannot do the integration
exactly. Look at the error you made using 10, 20, and 40 subintervals;
what is the relation of these errors?
Look at the handout on Approximate Convergence Order, and the
accompanying code. Are you getting the correct order of
convergence?