 and define
and define 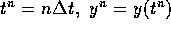 . If we know
. If we know
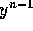 , we can advance to time
, we can advance to time  as follows.
as follows.
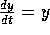 . It is easy enough to solve this
to find
. It is easy enough to solve this
to find  . That constant
is important; there are lots of solutions of the
differential equation, each with a different constant. We decide among
these solutions by specifying an initial condition. For example, if
. That constant
is important; there are lots of solutions of the
differential equation, each with a different constant. We decide among
these solutions by specifying an initial condition. For example, if
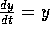 and
and 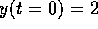 , then the solution
of the ``initial value problem'' is
, then the solution
of the ``initial value problem'' is
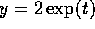 . Check this by differentiation.
. Check this by differentiation.
Our goal here is to develop methods for solving ODEs
numerically. In the example, we could integrate directly by
separating variables.
But in other cases, spearation of variables doesn't work, and
we need other techniques. We shall attack this problem by
discritizing the differentiated term. That is,
discritize time into subintervals of size
 and define
and define 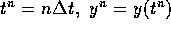 . If we know
. If we know
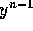 , we can advance to time
, we can advance to time  as follows.
as follows.

Solving for 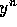 , we have
, we have

Clearly this algorithm lets us take timestep after timestep
(as long as 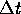 is small enough), ONCE WE GET STARTED.
But how do we take that very first step, from time
is small enough), ONCE WE GET STARTED.
But how do we take that very first step, from time 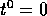 to time
to time 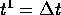 ? That is where the initial condition comes in.
The first step advances y from n=0 and looks just like
all the other steps, but we use the fact that at
? That is where the initial condition comes in.
The first step advances y from n=0 and looks just like
all the other steps, but we use the fact that at 
So the guts of a code would look like
dimension y(100),t(100)
.
.
Delta_t=0.001
.
.
t(1)=0.0
y(1)=2.0
do n=2,100
t(n)=t(n-1)+Delta_t
y(n)= (1.0 + Delta_t) * y(n-1)
enddo
This algorithm, known as Euler's method, is similar to a right-endpoint integration algorithm. But the Euler method can be used in more general settings. A major shortcoming of Euler's method, however is that it is only first order accurate. A version of the trapezoidal rule yields a second order method.
In the trapezoidal rule for integration, we averaged
the integrand at two points. In solving ODEs, we do not
have available the solution at the new time; after all, that's
what we are trying to find. We overcome this difficulty by
adopting what is called a predictor-corrector methodology.
We ``predict'' a new value for y using an Euler step; call it 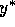 .
We then ``correct'' this prediction by solving the ODE
again, but this time averaging in y and t (if it were to appear).
The main loop would look like
.
We then ``correct'' this prediction by solving the ODE
again, but this time averaging in y and t (if it were to appear).
The main loop would look like
do n=2,100
t(n)=t(n-1)+Delta_t
ystar= (1.0+Delta_t) * y(n-1)
y(n)=y(n-1) + Delta_t * (y(n-1)+ystar)/2.0
enddo
There are higher order algorithms, the most common of which is a 4th order Runge-Kutta method. But we leave that for Mth/CS 437.
We now turn to systems of ODEs. For example, when the US Forest Service recently reintroduced wolves into Yellowstone National Park, they were (partly) motivated by population models for different animals -- predators like the wolf and prey like deer. Let W be the wolf population, D the deer population. These models typically take the form
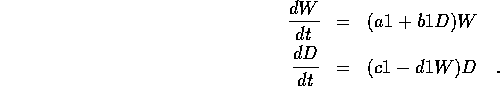
Here a1,b1,c1,d1 are positive constants relating to food supply, birth rate, and number of wolf-deer encounters.
An Euler algorithm (first order accurate) would look like
t(1)=0.d0
W(1)=W0
D(1)=D0
do n=2,100
t(n)=t(n-1)+Delta_t
W(n)= W(n-1) + Delta_t * (a1 + b1*D(n-1)) * W(n-1)
D(n)= D(n-1) + Delta_t * (c1 - d1*W(n-1)) * D(n-1)
enddo
We can again apply a trapezodial methodology to solve this system. We make a predictor step for both W and D, and then correct by averaging. Again, this algorithm works fine if the timestep is small enough, and gives second order accuracy.