


Next: About this document
Up: No Title
Previous: ODEs
- The function in the bisect.f evaluates
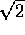 . Run the
code and check your answer (try the xcalc utility on the mouse).
Modify the function to compute
. Run the
code and check your answer (try the xcalc utility on the mouse).
Modify the function to compute  .
Find the three real roots of
.
Find the three real roots of
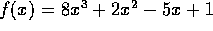 .
(You might want to use matlab's graphics routine to get a picture of
the cubic, to get estimates of where the roots lie.)
Then find the first 4 positive x-values where
.
(You might want to use matlab's graphics routine to get a picture of
the cubic, to get estimates of where the roots lie.)
Then find the first 4 positive x-values where  . (Zero is
obvisouly a solution; find the next 4 positive solutions.)
. (Zero is
obvisouly a solution; find the next 4 positive solutions.)
- Repeat (1) using false positions.
- Repeat (1) using Newton's method. For the
largest solution of
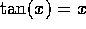 , try
initial guesses 13.0, 13.5, and 14.0. Can you explain what is happening?
, try
initial guesses 13.0, 13.5, and 14.0. Can you explain what is happening?
- Repeat (1) using the secant algorithm. You will need
a good secant method for a later exercise.
- Write a code using centered differences to
compute the approximate derivative of a function
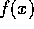 .
Test it thoroughly. Then incorporate it as a
subroutine into your Newton's method
code, instead of the function routine for fprime.
Use this new code to repeat exercise (1).
.
Test it thoroughly. Then incorporate it as a
subroutine into your Newton's method
code, instead of the function routine for fprime.
Use this new code to repeat exercise (1).
- Change the integration code so that it uses the
trapezodial rule. Check that this new method gives
exact answers if f is a constant or a line.
Then run the trapezodial algorithm for
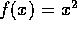 , using
10, then 20, then 40, then 80 subintervals.
Check the order of convergence; is it right? Now
compute
, using
10, then 20, then 40, then 80 subintervals.
Check the order of convergence; is it right? Now
compute 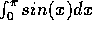 .
.
- A more challenging problem. Define
 .
For what x is
.
For what x is  ?
?
- Write a code implementing the trapezodial method
to solve the ODE
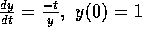 , up to t=1
A timestep of 1/20 ought to suffice. But to check yourself,
run the code using 1/20, 1/40 and 1/80 and make sure
you are getting (essentially) second order convergence.
, up to t=1
A timestep of 1/20 ought to suffice. But to check yourself,
run the code using 1/20, 1/40 and 1/80 and make sure
you are getting (essentially) second order convergence.
- Write a code to implement a trapezodial method for the
preditor-prey equations, for 0<t<10. Use a1=2.0, b1=0.1,
c1=3.0, d1=0.1, W(t=0) = 20.0,
D(t=0) = 20.0. Output your results in two files, listing
t and D in one file, t and W in the other. Use Matlab to
(1) on same plot, show D and W as functions of t
(2) show W vs. D. Now try changing W0 and D0 (e.g. (30,30),(20,30),(30,20)).
Can you tell what is going on?



Next: About this document
Up: No Title
Previous: ODEs
Bruce Pitman
Wed Oct 11 12:23:54 EDT 1995
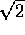 . Run the
code and check your answer (try the xcalc utility on the mouse).
Modify the function to compute
. Run the
code and check your answer (try the xcalc utility on the mouse).
Modify the function to compute  .
Find the three real roots of
.
Find the three real roots of
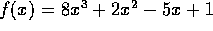 .
(You might want to use matlab's graphics routine to get a picture of
the cubic, to get estimates of where the roots lie.)
Then find the first 4 positive x-values where
.
(You might want to use matlab's graphics routine to get a picture of
the cubic, to get estimates of where the roots lie.)
Then find the first 4 positive x-values where  . (Zero is
obvisouly a solution; find the next 4 positive solutions.)
. (Zero is
obvisouly a solution; find the next 4 positive solutions.)
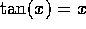 , try
initial guesses 13.0, 13.5, and 14.0. Can you explain what is happening?
, try
initial guesses 13.0, 13.5, and 14.0. Can you explain what is happening?
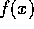 .
Test it thoroughly. Then incorporate it as a
subroutine into your Newton's method
code, instead of the function routine for fprime.
Use this new code to repeat exercise (1).
.
Test it thoroughly. Then incorporate it as a
subroutine into your Newton's method
code, instead of the function routine for fprime.
Use this new code to repeat exercise (1).
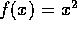 , using
10, then 20, then 40, then 80 subintervals.
Check the order of convergence; is it right? Now
compute
, using
10, then 20, then 40, then 80 subintervals.
Check the order of convergence; is it right? Now
compute 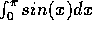 .
.
 .
For what x is
.
For what x is  ?
?
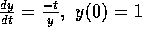 , up to t=1
A timestep of 1/20 ought to suffice. But to check yourself,
run the code using 1/20, 1/40 and 1/80 and make sure
you are getting (essentially) second order convergence.
, up to t=1
A timestep of 1/20 ought to suffice. But to check yourself,
run the code using 1/20, 1/40 and 1/80 and make sure
you are getting (essentially) second order convergence.