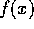There are several new ingredients in the code that we must explain.
The primary new structure is the function subroutine
used to compute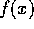 
. This structure is a special case of
the more general structure called subroutines, which we will
use later on. For the moment let us explain the function subroutine.
The general form for the function is
type function fntname(arg1,arg2,...)
real {rvarnames}
integer {ivarnames}
.
.
statements to compute auxillary values
.
fntname=.....
return
end
The type tells what type the function value is: integer, real, etc. The arguments arg1,arg2 are a list of variables to be used in the evaluation of fntname; in our example, there is but one argument, which is the x-value at which we wish to evaluate ff. In some circumstances, it may be necessary to execute auxillary statements before evaluating fntname; for instance, the following code fragment evaluates a piecewise-defined function, depending on whether x is positive or negative.
real function pdef(x)
implicit none
real x,pdef
if (x .gt. 0.0) then
pdef=sqrt(x+1.0)
else
pdef=sqrt(x**2)
endif
return
end
The bisection algorithm has its strong points and its weak points.
The major strength of the algorithm is that, providing we can find
the initial bracketing points a and b, the algorithm is
guaranteed to converge to a root, to within prescribed accuracy.
The major weak point of the algorithm is that its convergence rate
is slow -- no matter how close a and b are together, or to
a root, bisection (as its name implies) only improves the
guess by a factor of 
with each iteration.
There is a variant of bisection, called the method of false positions,
which often converges faster than bisection.