


Next: Newton's method
Up: No Title
Previous: Function subroutine
In false positions, instead of always using the midpoint of
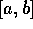 as the iteration point, you use the x-intercept
of the line between
as the iteration point, you use the x-intercept
of the line between 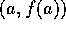 and
and 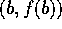 .
That is, given
.
That is, given  and
and  , compute the
equation of the line between these points;
, compute the
equation of the line between these points;
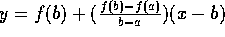 . Set y=0 and solve for
x to find the x-intercept; call this intercept c. So
. Set y=0 and solve for
x to find the x-intercept; call this intercept c. So
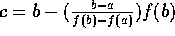 .
Now evaluate
.
Now evaluate 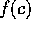 to determine whether it is
positive or negative, and keep either a or b depending on
the sign of
to determine whether it is
positive or negative, and keep either a or b depending on
the sign of 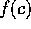 , just like in bisection.
, just like in bisection.
To change your bisection code into a false positions code, copy
bisect.f into another file, say falsa.f. Change the program name
and comment line to reflect the change to false positions.
The only line you need to change in the body of the code is
the definition of y. Instead of  , you need
to calculate the x-intercept, called c in the previous paragraph.
, you need
to calculate the x-intercept, called c in the previous paragraph.
Run both bisection and false positions to find 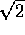 .
False position starts out slower than bisection -- after
the first two steps, the interval in which the root lies is smaller
under bisection. But once false positions gets close to the root,
it zips in quickly. So the method of false position shares with
bisection the advantage of trapping a root and, therefore, always
converging. But false position has a decided advantage in the
speed with which it converges.
.
False position starts out slower than bisection -- after
the first two steps, the interval in which the root lies is smaller
under bisection. But once false positions gets close to the root,
it zips in quickly. So the method of false position shares with
bisection the advantage of trapping a root and, therefore, always
converging. But false position has a decided advantage in the
speed with which it converges.
We next turn to another algorithm, Newton's method for
finding roots. Newton's method does not always converge. But,
when it does converge, it is very fast (at least once it is ``close
enough'' to the root). Newton's method also has the advantage of
not requiring a bracketing interval with positive and negative values
(so Newton's method will allow us to solve 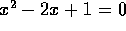 ,
whereas bisection and false positions will not).
,
whereas bisection and false positions will not).
Bruce Pitman
Wed Oct 11 12:23:54 EDT 1995
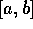 as the iteration point, you use the x-intercept
of the line between
as the iteration point, you use the x-intercept
of the line between 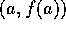 and
and 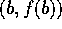 .
That is, given
.
That is, given  and
and  , compute the
equation of the line between these points;
, compute the
equation of the line between these points;
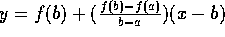 . Set y=0 and solve for
x to find the x-intercept; call this intercept c. So
. Set y=0 and solve for
x to find the x-intercept; call this intercept c. So
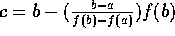 .
Now evaluate
.
Now evaluate 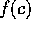 to determine whether it is
positive or negative, and keep either a or b depending on
the sign of
to determine whether it is
positive or negative, and keep either a or b depending on
the sign of 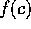 , just like in bisection.
, just like in bisection.
 , you need
to calculate the x-intercept, called c in the previous paragraph.
, you need
to calculate the x-intercept, called c in the previous paragraph.
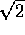 .
False position starts out slower than bisection -- after
the first two steps, the interval in which the root lies is smaller
under bisection. But once false positions gets close to the root,
it zips in quickly. So the method of false position shares with
bisection the advantage of trapping a root and, therefore, always
converging. But false position has a decided advantage in the
speed with which it converges.
.
False position starts out slower than bisection -- after
the first two steps, the interval in which the root lies is smaller
under bisection. But once false positions gets close to the root,
it zips in quickly. So the method of false position shares with
bisection the advantage of trapping a root and, therefore, always
converging. But false position has a decided advantage in the
speed with which it converges.
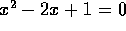 ,
whereas bisection and false positions will not).
,
whereas bisection and false positions will not).