
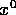 to a root of
to a root of  , a refined guess,
, a refined guess, 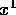 is
computed based on the x-intercept of the line tangent to
f at
is
computed based on the x-intercept of the line tangent to
f at 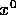 . That is, consider the equation of the
line tangent to f at
. That is, consider the equation of the
line tangent to f at 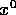 ,
,

This is the point-slope equation of a line, with
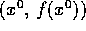 being the point and
being the point and  the slope.
Now calculate that x at which y=0. That is,
the slope.
Now calculate that x at which y=0. That is,
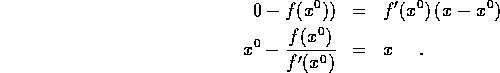
This value of x is the new guess at the root -- call it
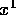 . We repeat the process, computing an
. We repeat the process, computing an
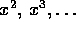 , until we compute an
, until we compute an 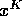 at which
at which
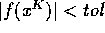 , where tol is a prescribed tolerance.
, where tol is a prescribed tolerance.
If you examine the formula for the new iterates 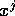 you can
see one potential for failure of Newton's method, namely
you can
see one potential for failure of Newton's method, namely
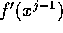 could be zero -- or, what is essentially the same, very
small. This may lead to wild divergences in the iteration procedure.
There are other possible failures in the method that we will uncover
in the exercises. For now, here is a skeleton code for Newton's method.
Notice you need formulae for both f and
could be zero -- or, what is essentially the same, very
small. This may lead to wild divergences in the iteration procedure.
There are other possible failures in the method that we will uncover
in the exercises. For now, here is a skeleton code for Newton's method.
Notice you need formulae for both f and  .
.