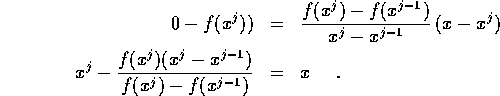Next: Numerical differentiation
Up: Newton's method
Previous: newton.f
As an exercise, try finding both roots of  using both
bisection and Newton's method; among your initial guesses,
try
using both
bisection and Newton's method; among your initial guesses,
try  . Then try
. Then try 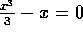 by both methods; try different initial guesses, including
by both methods; try different initial guesses, including
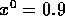 and
and 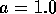 ,
,  . Does Newton's method
converge as you expect it to?
How can one prevent the potentially catastrophic
run-away of the approximates in Newton's method?
. Does Newton's method
converge as you expect it to?
How can one prevent the potentially catastrophic
run-away of the approximates in Newton's method?
The rapid convergence of Newton's method can be appreciated
by looking at how rapidly 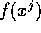 approaches zero. For example,
in solving
approaches zero. For example,
in solving  we have the following output:
we have the following output:
EBP on einstein> newt
Need an initial guess at the root
-0.9
To what tolerance ?
0.0000001
At iteration 1
x= -0.90000000000000 f(x) = 0.65700000000000
At iteration 2
x= 2.5578947368421 f(x) = 3.0207248870098
At iteration 3
x= 2.0129154847778 f(x) = 0.70574745863718
At iteration 4
x= 1.7816615328970 f(x) = 1.0352511682707D-01
At iteration 5
x= 1.7340488444577 f(x) = 4.0029910455239D-03
At iteration 6
x= 1.7320542555928 f(x) = 6.8960683805575D-06
The root is x= 1.7320508075792 with f(x) = 2.0592194616142D-11
EBP on einstein>
The first two iterations are not too good -- f is
nearer to 1 than to 0. But then at iteration 4,  ;
at iteration 5,
;
at iteration 5, 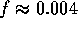 ; at iteration 6,
; at iteration 6,  ;
at the last iteration,
;
at the last iteration, 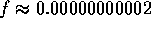 . Thus, on successive
iterations,
. Thus, on successive
iterations, 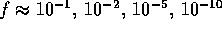 ,
a doubling (approximately) with each iteration.
The values of the x-iterates show the same doubling.
Taking
,
a doubling (approximately) with each iteration.
The values of the x-iterates show the same doubling.
Taking 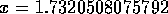 as the ``correct'' answer, we see
that, beginning with iteration 4, the successive x's have
1, then 2, then 5 correct digits to the right of the decimal point.
This doubling is referred to as quadratic convergence.
as the ``correct'' answer, we see
that, beginning with iteration 4, the successive x's have
1, then 2, then 5 correct digits to the right of the decimal point.
This doubling is referred to as quadratic convergence.
What is a soul to do if 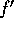 is not easily evaluated?
There are two related options available to you. Both options
estimate the derivative of f somehow. The first option
is called the secant algorithm. Instead of starting with one
initial guess,
is not easily evaluated?
There are two related options available to you. Both options
estimate the derivative of f somehow. The first option
is called the secant algorithm. Instead of starting with one
initial guess,  , start with two,
, start with two, 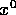 and
and 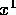 (not
unlike the bisection and false position algorithms).
Now draw the line between these
points (the secant line), and determine the x-intercept of this
line. This x-intercept is the new approximate root
(say
(not
unlike the bisection and false position algorithms).
Now draw the line between these
points (the secant line), and determine the x-intercept of this
line. This x-intercept is the new approximate root
(say  ). Repeat the process using
). Repeat the process using
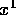 and
and 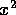 to find
to find  , and so on.
The formula for the secant algorithm is
, and so on.
The formula for the secant algorithm is
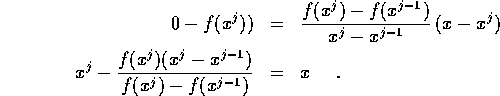
You should be able to modify your Newton's method code
into a secant algorithm code without too much work.
NOTE: This secant algorithm is very much like false positions. However,
in the former, one always uses the most recent updates; in the latter,
one always keeps the root bracketed. There are pros and cons to
each method.



Next: Numerical differentiation
Up: Newton's method
Previous: newton.f
Bruce Pitman
Wed Oct 11 12:23:54 EDT 1995
 using both
bisection and Newton's method; among your initial guesses,
try
using both
bisection and Newton's method; among your initial guesses,
try  . Then try
. Then try 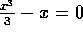 by both methods; try different initial guesses, including
by both methods; try different initial guesses, including
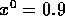 and
and 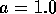 ,
,  . Does Newton's method
converge as you expect it to?
How can one prevent the potentially catastrophic
run-away of the approximates in Newton's method?
. Does Newton's method
converge as you expect it to?
How can one prevent the potentially catastrophic
run-away of the approximates in Newton's method?
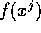 approaches zero. For example,
in solving
approaches zero. For example,
in solving  we have the following output:
we have the following output:
 ;
at iteration 5,
;
at iteration 5, 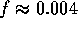 ; at iteration 6,
; at iteration 6,  ;
at the last iteration,
;
at the last iteration, 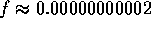 . Thus, on successive
iterations,
. Thus, on successive
iterations, 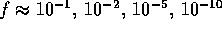 ,
a doubling (approximately) with each iteration.
The values of the x-iterates show the same doubling.
Taking
,
a doubling (approximately) with each iteration.
The values of the x-iterates show the same doubling.
Taking 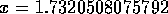 as the ``correct'' answer, we see
that, beginning with iteration 4, the successive x's have
1, then 2, then 5 correct digits to the right of the decimal point.
This doubling is referred to as quadratic convergence.
as the ``correct'' answer, we see
that, beginning with iteration 4, the successive x's have
1, then 2, then 5 correct digits to the right of the decimal point.
This doubling is referred to as quadratic convergence.
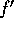 is not easily evaluated?
There are two related options available to you. Both options
estimate the derivative of f somehow. The first option
is called the secant algorithm. Instead of starting with one
initial guess,
is not easily evaluated?
There are two related options available to you. Both options
estimate the derivative of f somehow. The first option
is called the secant algorithm. Instead of starting with one
initial guess,  , start with two,
, start with two, 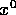 and
and 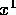 (not
unlike the bisection and false position algorithms).
Now draw the line between these
points (the secant line), and determine the x-intercept of this
line. This x-intercept is the new approximate root
(say
(not
unlike the bisection and false position algorithms).
Now draw the line between these
points (the secant line), and determine the x-intercept of this
line. This x-intercept is the new approximate root
(say  ). Repeat the process using
). Repeat the process using
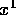 and
and 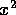 to find
to find  , and so on.
The formula for the secant algorithm is
, and so on.
The formula for the secant algorithm is