


Next: bisect.f
Up: No Title
Previous: No Title
If we (somehow) knew that a root of f lies
in the interval  , then by doing some figuring,
we might be able to squeeze down the size of the
interval (e.g. cut it in half) in which the root lies. That idea
is the heart of the bisection method.
, then by doing some figuring,
we might be able to squeeze down the size of the
interval (e.g. cut it in half) in which the root lies. That idea
is the heart of the bisection method.
The restriction under
which we operate is that  and
and 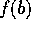 must have opposite signs --
one of them must be positive, the other negative. Then, because
f is continuous (we have to assume that), there must be a zero of
f somewhere in
must have opposite signs --
one of them must be positive, the other negative. Then, because
f is continuous (we have to assume that), there must be a zero of
f somewhere in 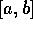 . Let c be the midpoint of
. Let c be the midpoint of
 . Either c is the root, or the root lies in
. Either c is the root, or the root lies in
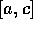 or the root lies in
or the root lies in  .
Which happens? Well, we can evaluate
.
Which happens? Well, we can evaluate
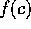 . If it is a zero (or at least if it is sufficiently small),
we have our root. If it is not zero, then
one pair of
. If it is a zero (or at least if it is sufficiently small),
we have our root. If it is not zero, then
one pair of 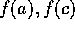 or
or 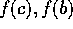 have opposite signs.
Keep the half-interval with opposite signs. Repeat the process
until either
have opposite signs.
Keep the half-interval with opposite signs. Repeat the process
until either  f, evaluated at the midpoint of the interval,
is sufficiently small (less than a tolerance we must prescribe),
or
f, evaluated at the midpoint of the interval,
is sufficiently small (less than a tolerance we must prescribe),
or  the interval has been shrunk sufficiently small
(less than a second prescribed tolerance).
That is the bisection algorithm.
the interval has been shrunk sufficiently small
(less than a second prescribed tolerance).
That is the bisection algorithm.
Bruce Pitman
Wed Oct 11 12:23:54 EDT 1995
 and
and 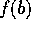 must have opposite signs --
one of them must be positive, the other negative. Then, because
f is continuous (we have to assume that), there must be a zero of
f somewhere in
must have opposite signs --
one of them must be positive, the other negative. Then, because
f is continuous (we have to assume that), there must be a zero of
f somewhere in 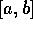 . Let c be the midpoint of
. Let c be the midpoint of
 . Either c is the root, or the root lies in
. Either c is the root, or the root lies in
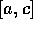 or the root lies in
or the root lies in  .
Which happens? Well, we can evaluate
.
Which happens? Well, we can evaluate
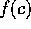 . If it is a zero (or at least if it is sufficiently small),
we have our root. If it is not zero, then
one pair of
. If it is a zero (or at least if it is sufficiently small),
we have our root. If it is not zero, then
one pair of 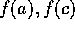 or
or 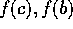 have opposite signs.
Keep the half-interval with opposite signs. Repeat the process
until either
have opposite signs.
Keep the half-interval with opposite signs. Repeat the process
until either  f, evaluated at the midpoint of the interval,
is sufficiently small (less than a tolerance we must prescribe),
or
f, evaluated at the midpoint of the interval,
is sufficiently small (less than a tolerance we must prescribe),
or  the interval has been shrunk sufficiently small
(less than a second prescribed tolerance).
That is the bisection algorithm.
the interval has been shrunk sufficiently small
(less than a second prescribed tolerance).
That is the bisection algorithm.
 , then by doing some figuring,
we might be able to squeeze down the size of the
interval (e.g. cut it in half) in which the root lies. That idea
is the heart of the bisection method.
, then by doing some figuring,
we might be able to squeeze down the size of the
interval (e.g. cut it in half) in which the root lies. That idea
is the heart of the bisection method.