In today's information age, there are usually several sources of information that describe different properties or characteristics of individual objects. On each of the information source, a relationship graph can be derived to characterize the pairwise similarities between objects where the edge weight indicates the degree of similarity. As an example, the following figure shows the similarity relationships among a set of movies derived from two information sources: movie genres and users. The genre information may indicate that two movies that are "animations" are more similar than two movies one of which is an "animation" and one of which is a "romance" movie. Similarly, movies watched by the same set of users are likely to be more similar than movies that are watched by completely different sets of users.

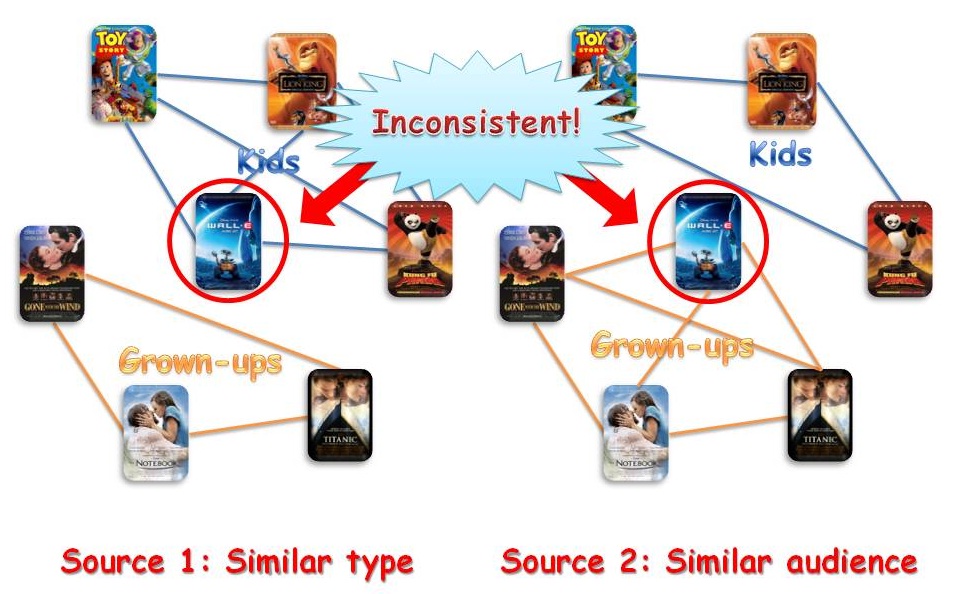
Clearly, objects form a variety of clusters or communities based on each similarity relationship. For example, two clusters can be found from both of the similarity graphs in the above figure. One cluster represents the movies that are animations, which are loved by kids; while the other cluster represents romance movies, which are liked by grown-ups. Most of the movies belong to the same cluster even though different information sources are used. However, there are some objects that fall into different clusters with respect to different sources. In this example, movie "Wall-E" by genre is liked by kids, but is liked by grown-ups based on the user watching history, and thus it is likely to be a horizontal anomaly. Finding such "inconsistent" movies can help film distributors better understand the expected audiences of different movies and make smarter marketing plans.

Some example scenarios of horizontal anomaly detection are listed as follows. 1) In social networks, detecting people who fall into different social communities with respect to different online social networks would be interesting for user behavior analysis; 2) In bioinformatics, inconsistencies across different gene-gene interaction similarity graphs derived from patients with and without a certain disease represent the genes which are critical to the disease; 3) For better business marketing, one wants to find out the person who bought quite different items compared with his peers in the same social community based on the two information sources drawn from user purchase history and friendship networks; and 4) Inconsistencies across multiple module interaction graphs derived from different versions of a software project can be used to assist programmers. Besides the examples discussed above, identifying horizontal anomalies across multiple sources can find applications in many other fields including smarter planet, internet of things, intelligent transportation systems, marketing, banking, etc.

We assume that each individual information source captures some similarity relationships between objects that may be represented in the form of a similarity matrix. We combine the input matrices into one matrix that captures the information from each source, but also ensures that individual object relationships are preserved. We then adopt spectral techniques to identify the key eigenvectors of the graph Laplacian of the combined matrix, and identify horizontal anomalies by computing cosine distance between the components of these eigenvectors. We give theoretical interpretations of the proposed method from both spectral clustering and random walk perspectives, and validate the proposed algorithm on both synthetic and real data sets.