Many real applications, such as network traffic monitoring, credit card fraud detection, and web click stream, generate continuously arriving data, known as data streams. To help decision making, we want to correctly classify an incoming data record based on the model learnt from historical labeled data. The challenge is the existence of distribution evolution or concept drifts, where one actually may never know either how or when the distribution changes.

Formally, we denote the feature vector and class label as x and y respectively. Data stream could be defined as an infinite sequence of (x; y). Training set D and test set T are two sets of sequentially adjacent examples drawn from the data stream. The labels in T are not known during classification process and will only be provided after some period of time. When learning from stream data, it is unlikely that training and testing data always come from the same distribution. This phenomenon hurts existing algorithms that are based upon such an assumption. Some stream mining work has investigated the change detection problem or utilized the concept change in model construction. However, since there are only unlabeled examples available in the test data set, the "change detection" could at most detect feature change. It is rather difficult to detect the change in P(y|x) before class labels are given. Therefore, strong assumptions are no good for stream mining, and any single learning method on data streams focusing on how to match the training distribution effectively may fail for a continuously changing data stream. We proposed a robust model averaging framework combining multiple supervised models, and demonstrated both formally and empirically that it can reduce generalization errors and outperform single models on stream data.

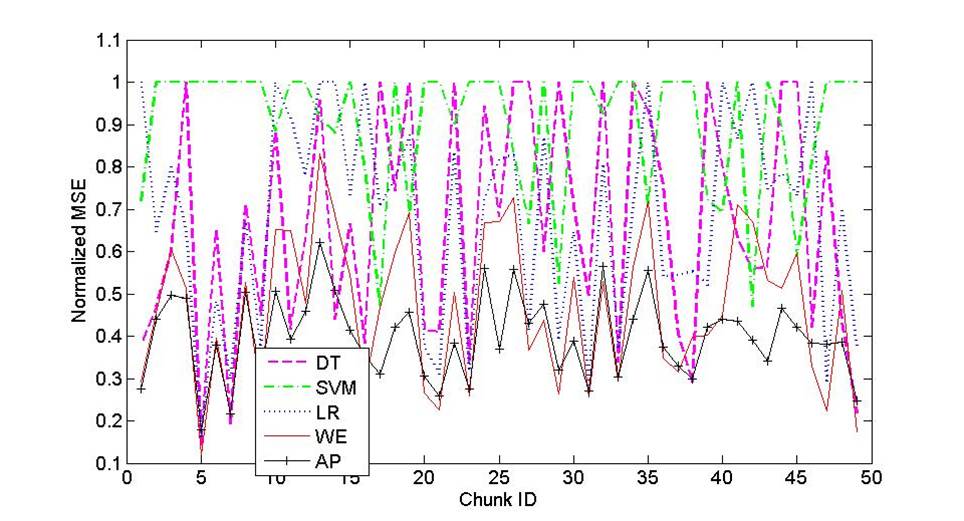
The following plot shows the classification error (normalized) of several methods on 50 time windows of stream data. As can be seen, the proposed ensemble method (AP) is the most accurate classifier in general. As measures of single models (DT, SVM, LR) fluctuate within a wide range, the performance of the proposed ensemble method is much more stable. The baseline ensemble approach (WE) could achieve higher accuracy than single-model classifiers but still has larger variance and worse average performance compared with AP. This clearly shows the benefits of using our ensemble framework when the testing distribution is unknown and departed from the training distribution.

We also considered a more challenging situation in stream mining, where the class distributions in the data are skewed, i.e, few positives but lots of negatives, such as intrusions (positives) and normal records (negatives) in network traffic data. In these applications, misclassifying a positive object usually invokes a much higher loss compared to that of misclassifying a negative object. Therefore, traditional classification algorithms, which tend to ignore positive objects and predict every object as negative, is undesirable for skewed stream mining.

We assume that incoming data stream arrive in sequential batches. The aim of stream classification is to train a classifier based on the data arrived so far to estimate posterior probabilities of objects in the most recent time window. In this problem, we further assume that data come from two classes, positive and negative classes, and the number of objects in negative class is much greater than the number of positive objects. We propose to utilize both sampling and ensemble techniques in our framework.

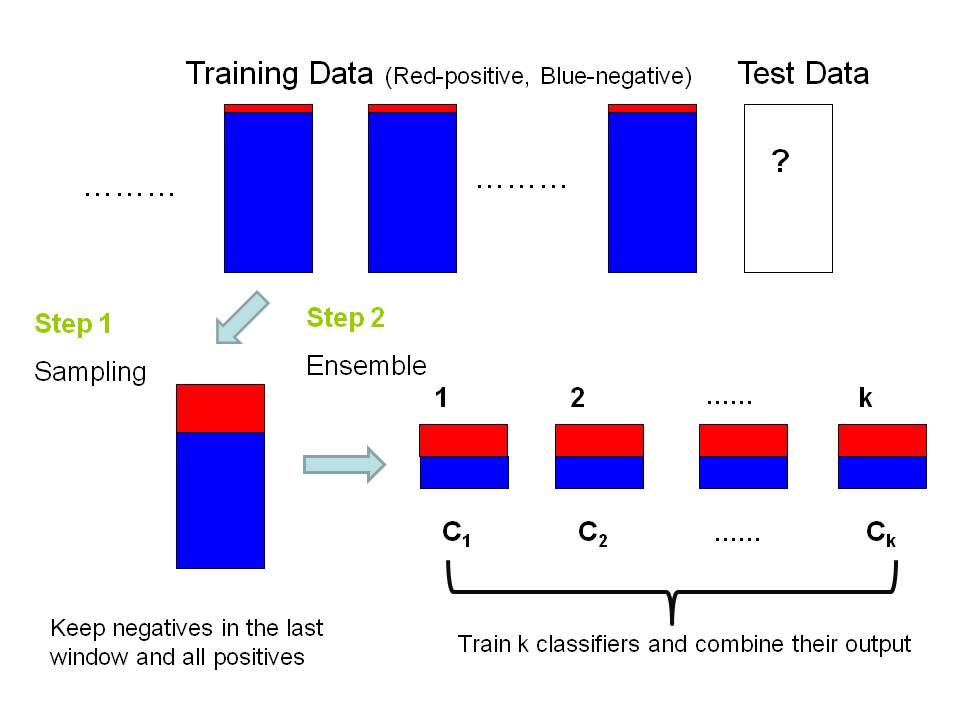
Sampling. In stream mining, we cannot use all the historical data as training data. First, stream data are huge in amount and it is usually impossible to store all of them. Second, stream mining requires fast processing, but a huge training set will make the classification process extremely slow, thus is unsatisfactory. The usual practice is to build the model upon data in the most recent time window. This works for objects in negative class since they dominate the data chunk and are sufficient for training an accurate model. However, the positive objects are far from sufficient. A classifier built on data from one time window will perform poorly on positive class. To enhance the set of positive examples, we propose to collect all positive examples seen so far and keep them in the training set, as illustrated in the following figure.

Ensemble. Instead of training a single model on this training set, we propose to generate multiple samples from the training set, compute and combine multiple models from these samples. The accuracy of ensemble method is usually higher than that of a single model trained from the entire dataset on average. In fact, when the samples are more uncorrelated, it is more likely that the base classifiers make uncorrelated errors which could be eliminated by averaging. To get uncorrelated samples, each negative object in the training set is randomly propagated to exactly one sample, hence the negative objects in the samples are completely disjoint. As for positive objects, they are propagated to each sample. We then train a classifier from each sample and combine the predictions.