Table of contents

Mobile Robot Mapping

Motivation for Mapping

Background to Mapping

Conventional Notation

Canonical form of map building, map given set of sensor measurements and corresponding poses

\begin{equation*} p(X_{1 \ldots t}, M | Z_{1 \ldots t}) \end{equation*}

Recast by Bayes' theorem

\begin{equation*} p(Z_{1 \ldots t} | X_{1 \ldots t}, M ) p(X_{1 \ldots t}, M) / p(Z_{1 \ldots t}) \end{equation*}

Mapping with known poses

Mapping with known poses

Scan matching

Typical convergence path http://www.youtube.com/watch?v=LlevpwUrWkE

Loop Closure

A Heuristic Loop Closing Technique for Large-Scale 6D SLAM by J. Sprickerhof, A. Nüchter, K. Lingemann, and J. Hertzberg

Iterative Closest Point, ICP

Original paper [besl1992]

ICP Algorithm

Point-to-point ICP derivation

For a rotation about the x-axis

Given the rotation matrices around the various axes.

\begin{equation*} R_x(\theta) = \left( \begin{matrix} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta \\ 0 & \sin \theta & \cos \theta \\ \end{matrix} \right), R_y(\theta) = \left( \begin{matrix} \cos \theta & 0 & \sin \theta \\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \\ \end{matrix} \right), R_z(\theta) = \left( \begin{matrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0\\ 0 & 0 & 1\\ \end{matrix} \right), \end{equation*}

The full rotation matrix for small angles \(\alpha, \beta, \gamma\) about the \(x, y, z\) axes is therefore

\begin{equation*} R = \left( \begin{matrix} 1 & -\gamma & \beta \\ \gamma & 1 & -\alpha \\ -\beta & \alpha & 1 \\ \end{matrix} \right) \end{equation*}

The rotation matrix,

\begin{equation*} R =\left(\begin{matrix}1 & - \gamma & \beta\\\gamma & 1 & - \alpha\\- \beta & \alpha & 1\end{matrix}\right) \end{equation*}

The translation vector

\begin{equation*} T =\left(\begin{matrix}t_{x}\\t_{y}\\t_{z}\end{matrix}\right) \end{equation*}

The error function

\begin{equation*} E = R P + T - Q =\left(\begin{matrix}p_{x} + t_{x} - q_{x} + \beta p_{z} - \gamma p_{y}\\p_{y} + t_{y} - q_{y} + \gamma p_{x} - \alpha p_{z}\\p_{z} + t_{z} - q_{z} + \alpha p_{y} - \beta p_{x}\end{matrix}\right) \end{equation*}
\begin{equation*} =\left(p_{x} + t_{x} - q_{x} + \beta p_{z} - \gamma p_{y}\right)^{2} + \left(p_{y} + t_{y} - q_{y} + \gamma p_{x} - \alpha p_{z}\right)^{2} + \left(p_{z} + t_{z} - q_{z} + \alpha p_{y} - \beta p_{x}\right)^{2} \end{equation*}

To minimise E equate partial derivatives to zero.

\begin{equation*} \delta E / \delta \alpha = p_{y} t_{z} + p_{z} q_{y} - p_{y} q_{z} - p_{z} t_{y} - \beta p_{x} p_{y} - \gamma p_{x} p_{z} + \alpha p_{y}^{2} + \alpha p_{z}^{2} = 0 \end{equation*}
\begin{equation*} \delta E / \delta \beta = p_{x} q_{z} + p_{z} t_{x} - p_{x} t_{z} - p_{z} q_{x} - \alpha p_{x} p_{y} - \gamma p_{y} p_{z} + \beta p_{x}^{2} + \beta p_{z}^{2} = 0 \end{equation*}
\begin{equation*} \delta E / \delta \gamma = p_{x} t_{y} + p_{y} q_{x} - p_{x} q_{y} - p_{y} t_{x} - \alpha p_{x} p_{z} - \beta p_{y} p_{z} + \gamma p_{x}^{2} + \gamma p_{y}^{2} = 0 \end{equation*}
\begin{equation*} \delta E / \delta t_x = p_{x} + t_{x} - q_{x} + \beta p_{z} - \gamma p_{y} = 0 \end{equation*}
\begin{equation*} \delta E / \delta t_y = p_{y} + t_{y} - q_{y} + \gamma p_{x} - \alpha p_{z} = 0 \end{equation*}
\begin{equation*} \delta E / \delta t_z = p_{z} + t_{z} - q_{z} + \alpha p_{y} - \beta p_{x} = 0 \end{equation*}

Factor out the coefficients of the DOFs appropriately so it can be represented in linear form for solving.

\begin{equation*} A x + B = 0 \end{equation*}

Results in a covariance like matrix and linear matrix equation

\begin{equation*} \left(\begin{matrix}p_{y}^{2} + p_{z}^{2} & - p_{x} p_{y} & - p_{x} p_{z} & 0 & - p_{z} & p_{y}\\- p_{x} p_{y} & p_{x}^{2} + p_{z}^{2} & - p_{y} p_{z} & p_{z} & 0 & - p_{x}\\- p_{x} p_{z} & - p_{y} p_{z} & p_{x}^{2} + p_{y}^{2} & - p_{y} & p_{x} & 0\\0 & p_{z} & - p_{y} & 1 & 0 & 0\\- p_{z} & 0 & p_{x} & 0 & 1 & 0\\p_{y} & - p_{x} & 0 & 0 & 0 & 1\end{matrix}\right) \left(\begin{matrix}\alpha\\\beta\\\gamma\\t_{x}\\t_{y}\\t_{z}\end{matrix}\right)+\left(\begin{matrix}p_{z} q_{y} - p_{y} q_{z}\\p_{x} q_{z} - p_{z} q_{x}\\p_{y} q_{x} - p_{x} q_{y}\\p_{x} - q_{x}\\p_{y} - q_{y}\\p_{z} - q_{z}\end{matrix}\right)= 0 \end{equation*}

Alternative ICP methods

Mapping in 3D

Map representations

Occupancy grid update derivation

Canonical form of map building, map given set of sensor measurements and corresponding poses

\begin{equation*} p(M|z_1, \ldots, z_T) \end{equation*}

Under first-order Markov assumption

\begin{equation*} p(m_k|m_0, \ldots, m_{k-1}) = p (m_k|m_{k-1}) p(z_k|m_0, \ldots, m_k) = p(z_k|m_k). \end{equation*}

Applying these assumptions gives rise to

\begin{equation*} p(m_0, \ldots, m_k, z_1, \ldots, z_k)=p(m_0) \prod_{i=1}^k p(z_i|m_i) p(m_i|m_{i-1}) \end{equation*}

Finally, this produces

\begin{equation*} p(m_k| z_1, \ldots, z_k)=\frac{p(z_k|m_k)p(m_k|z_1, \ldots, z_{k-1})} {p(z_k|z_1, \ldots, z_{k-1})} \end{equation*}

which only holds if the environment is time invariant.

For a particular map cell, m, and laser return cell, l

\begin{equation*} p(m|l)=\left( 1 + \frac{p(l|\neg m) p(\neg m)}{p(l|m)p(m)} \right) ^{-1} \end{equation*}

The log odds approach to probabilities simplifies the update step enhances the expressive power of the map, which often contains probabilities close to either 1 or 0

The odds of an event A

\begin{equation*} o(A) = \frac{p(A)}{p(\neg A)} = \frac{p(A)}{1 - p(A)}, \end{equation*}

and conversely probabilities can be calculated from the odds as

\begin{equation*} p(A) = \frac{o(A)}{1 + o(A)}. \end{equation*}

Thus the map update can be expressed as

\begin{equation*} o(m|l) = \frac{p(l|m) p(m)}{p(l|\neg m) p(\neg m)} = \frac{p(l|m)}{p(l|\neg m)} o(m) \end{equation*}

Therefore in terms of log odds

\begin{equation*} \log o(m|l) = \log \frac{p(l|m)}{p(l|\neg m)} + \log o(m) = \log p(l|m) - \log {p(l|\neg m)} + \log o(m) \end{equation*}

Odometry/Dead reckoning

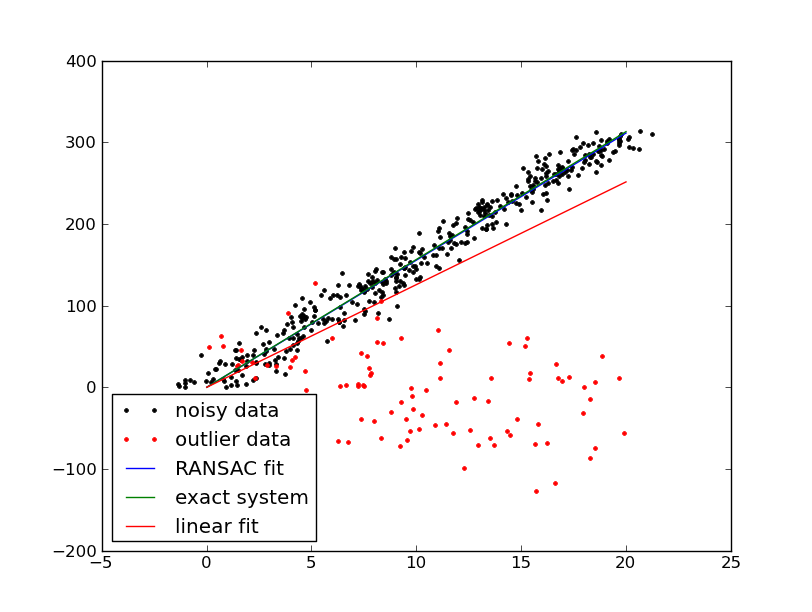
RANdom SAmple Consensus, RANSAC

RANSAC pseudocode

while iterations < k
    maybe_inliers := n randomly selected values from data
    maybe_model := model parameters fitted to maybe_inliers
    consensus_set := maybe_inliers

    for every point in data not in maybe_inliers
        if point fits maybe_model with an error smaller than t
            add point to consensus_set

    if the number of elements in consensus_set is > d
        (this implies that we may have found a good model,
        now test how good it is)
        this_model := model parameters fitted to all points in consensus_set
        this_error := a measure of how well this_model fits these points
        if this_error < best_error
            (we have found a model which is better than any of the previous ones,
            keep it until a better one is found)
            best_model := this_model
            best_consensus_set := consensus_set
            best_error := this_error

    increment iterations

RANSAC Illustration

images/ransac_example.png

Feature extraction

Various levels of feature extraction

Current research

/jcr/active/edgevoxels/figures/mason2011_hallway_map.png /jcr/active/edgevoxels/figures/mason2011_hallway_edgemap.png

References

Simultaneous Localisation and Mapping (SLAM): Part I The Essential Algorithms Hugh Durrant-Whyte, Fellow, IEEE, and Tim Bailey

[besl1992]A method for registration of 3D shapes
Mobile Robot Mapping - Julian Ryde