The problem

Given a graph $G$ and a number $k$, does $G$ contain a clique of size at least $k$? I.e. does there exists a subset $S\subseteq V$ such that $|S|=k$ and there are all possible $\binom{k}{2}$ edges present among the vertices in $S$?

Sample Input/Output pairs

For the sample inputs, let us consider the following graph, which we will call $G_0$:

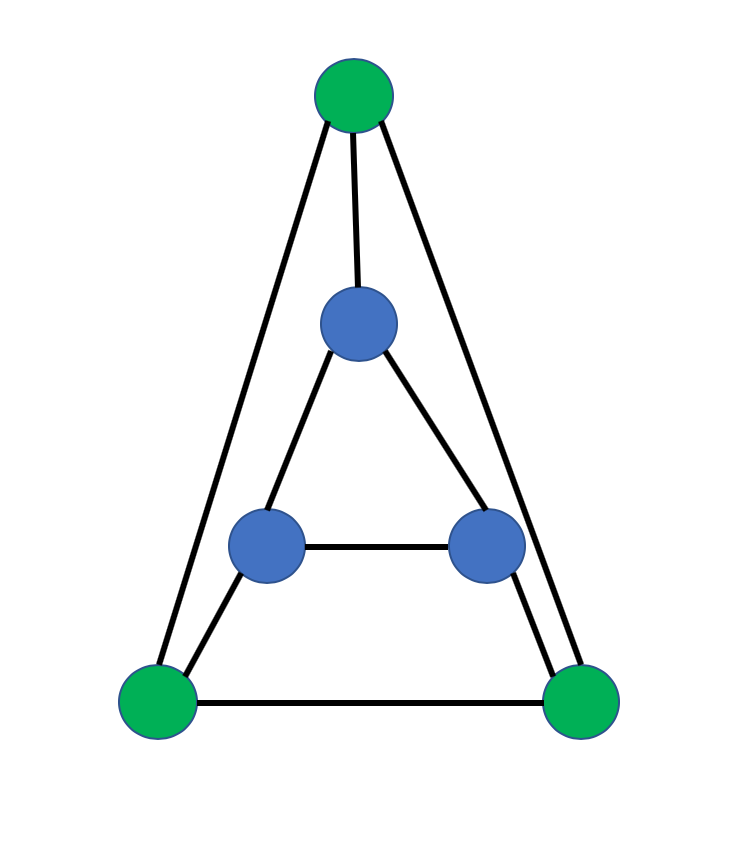
• Input: $G_0, 3$
• Output: true (Consider the three blue nodes)

• Input: $G_0, 4$
• Output: false (Every subset of 4 nodes has at least 2 out of the 6 edges missing)

There are two parts to the problem:

• Part (a): Show that the Clique problem is in $\mathcal{NP}$.
• Part (b): Show that the Clique problem is $\mathcal{NP}$-complete.

  Hint

  It might be useful to consider the complement graph of $G$ and figure out what a clique in $G$ looks like in its complement. (The complement of $G=(V,E)$ is the graph $H=(V,E')$, where $(u,v)\in E'$ if and only if $(u,v)\not\in E$: i.e. if an edge is present in $G$, then it not present in $H$ and if an edge is not present in $G$, then it is present in $H$.)

The problem

Given a graph $G$, output a largest clique of $G$, i.e., the output $S$ should be a clique and it must be the case that $G$ does not have a clique of size $|S|+1$.

In this problem we will see how one can reduce the MaxClique problem to the Clique problem (from Question 1). There are two parts to the problem.

• Part (a): For this part, assume that we are interested in the simpler problem of outputting the size of a largest clique in $G$ (instead of actually outputting a largest clique). Further, assume that the Clique problem from Question 1 can be solved in time $T(n)$ on any graph of size $G$ (and any value of $k$).
  • Sub-part (1): Show that one can compute the size of a largest clique in time $O(n\cdot T(n))$.
  • Sub-part (2): Show that one can compute the size of a largest clique in time $O(\log{n}\cdot T(n))$.
• Part (b): Assume that the Clique problem from Question 1 is in $\mathcal{P}$. Show that then the MaxClique problem is also in $\mathcal{P}$ (i.e. there exists a polynomial time algorithm to solve the MaxClique problem). In other words, you want to argue that the Clique problem from Question 1 is essentially "as hard as" the MaxClique problem.

  Hint

  Note that since Clique is in $\mathcal{P}$, there exists a polynomial time algorithm $\mathcal{A}$ to solve that problem. Think of how you can call $\mathcal{A}$ multiple times to solve the MaxClique problem.

The Problem

In this problem we will explore the problem of reducing the graph $k$-colorability problem to SAT and then use a SAT solver to solve the $k$-colorability problem.

The graph $k$-colorability problem is as follows: Given an integer $k$ and an undirected, unweighted graph $G$, can you color $G$ using $k$ colors such that no two adjacent nodes have the same color? You will first generate a CNF formula to represent the constraints of this problem using the data structure explained in the Output section below. This CNF formula will get converted by our grading code to the format accepted by the SAT solver, and finally fed as input to the solver.

The solver outputs a variable assignment from which we can deduce what color a node was assigned if the constraints you create can be satisfied, and UNSAT if not. The solver output format is explained in the Solver output section below. Note that you do not need to concern yourself with the solver output format, but it could be extremely useful if you decide to play around with the solver by feeding it CNF formulas of your own. Further details are provided in the directory structure section of your preferred language below.

Input

The input file is given with the first line as the value of $k$ (the number of available colors) and the remainder of the file is an adjacency list for graph $G$ (we assume that the set of vertices is $\{0,1,\dots,n-1\}$). The adjacency list assumes that the current node is the index of the line under consideration. For instance line 0 of the input file (not including the value of $k$) has the list of all nodes adjacent to node 0.

                k		<- Value of k (No. of colors available)
                u1 u4 u6		<- All nodes that share edges with u0
            	u3 u4		<- All nodes that share edges with u1
		u0		<- All nodes that share edges with u2
		.
		.
		.
		u0 u4 u2 u7 	<- All nodes that share edges with un-1
	    

For example:

            	2		<- k
	 	1 2		<- Node 0 shares an edge with nodes 1 & 2
		0    		<- Node 1 shares an edge with node 0
		0		<- Node 2 shares an edge with node 0
	    

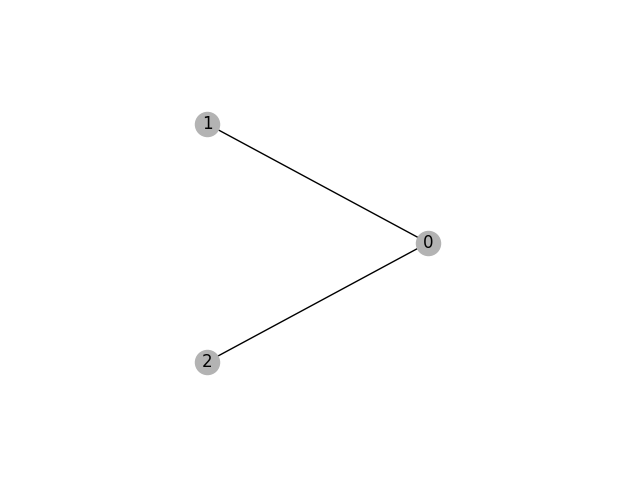
If we draw the graph using the above input, it will look like this:

Note that in this case, it is indeed possible to color the graph with two colors. Say you color node $0$ with color $1$, color nodes $1$ and $2$ with color $2$. Alternatively, color node $0$ with color $2$ and nodes $1$ and $2$ with color $1$. (Since nodes $1$ and $2$ are not connected by an edge, we can assign the same color to both of them.)

Let us now consider another example:

            	2		<- k
	 	1 2		<- Node 0 shares an edge with nodes 1 & 2
		0 2   		<- Node 1 shares an edge with nodes 0 & 2
		0 1		<- Node 2 shares an edge with nodes 0 & 1
	    

If we draw the graph using the above input, it will look like this:

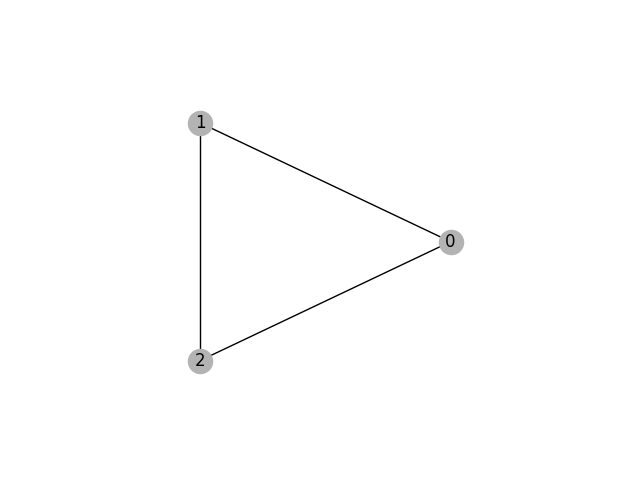
In this case, it is not possible to color the graph with two colors. Say you assign two different colors to nodes $0$ and $1$, which is necessary since they are connected by an edge, $2$ will have to be assigned a third color since it is connected to both $0$ and $1$. However, we only have two colors at hand. Changing the value of $k$ to $3$ will cause this to become satisfiable, however, since we can then color all the nodes with the three different colors.

Output

Your method is expected to return a list (outer) of tuples (outer) of two lists (inner) of two-element tuples (inner) of int (shudder).
The above list will represent the constraints of the k-colorability problem.

[([(0, 1), (0, 2)], [])]

[([], [(0, 1), (0, 2)])]

The output you generate above is fed into a SAT solver as explained in the Problem section. Then Autolab will check if the output of the SAT solver in your generated SAT formula correctly determines if the graph is not $k$-colorable and if it is, if the output gives a valid $k$-coloring.

Solver Output

The solver output is a list of integers which for this particular problem represent a particular flattened (node, color) pair formatted as your language of choice's array-type data structure (see below for the exact details). Note that nodes are 0-indexed while colors are 1-indexed.

            	[
                    v01,                                         Node 0 is assigned color c1 if v01 > 0
                    v02,                                         Node 0 is assigned color c2 if v02 > 0
                    ...                                          ...
                    v0k,                                         Node 0 is assigned color ck if v0k > 0
                    v11,                                         Node 1 is assigned color c1 if v11 > 0
                    ...                                          ...
                    v(n-1)k                                       Node (n-1) is assigned color ck if v(n-1)k > 0
                ]

	    

For example, using the first example input from above: (every pair represents a node)

                [
                    1, -2,                                      Node 0 is assigned color c1
                    -3, 4,                                      Node 1 is assigned color c2
                    -5, 6                                       Node 2 is assigned color c2
                ]

	       

OR

                [
                    -1, 2,                                      Node 0 is assigned color c2
                    3, -4,                                      Node 1 is assigned color c1
                    5, -6                                       Node 2 is assigned color c1
                ]

          

Note that the actual output (on Autolab) will look something like:

s SATISFIABLE                           <- Whether the given set of constraints is satisfiable
v -1 2 3 -4 5 -6 0                      <- Variable assignments, the 0 marks the end of the output (it is not a variable/literal).
                                           There will be multiple such lines if there are a lot of clauses.
             

For the second example input, the output will simply be:

s UNSATISFIABLE