Recitation 12
Recitation notes for the week of April 16, 2025.
A Reminder for HW 7 Q3
Note on Timeouts on HW 7 Q3
For this problem the total timeout for Autolab is 480s, which is higher the the usual timeout of 180s in the earlier homeworks. So if your code takes a long time to run it'll take longer for you to get feedback on Autolab. Please start early to avoid getting deadlocked out before the feedback deadline.
Also for this problem, C++ and Java are way faster. The 480s timeout was chosen to accommodate the fact that Python is much slower than these two languages.
Our recommendation
- Either code in
C++orjavaOR - If you want to program in
pythonthen test on first five test cases and test for all 10 only if they pass the first five.
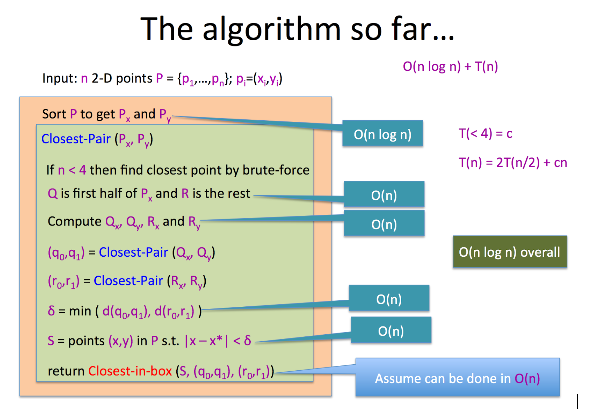
Closest Pair of Points Algorithm
The goal is to find the closest pair of points in a plane in $O(n\log{n})$ time.
Brute Force Algorithm Idea
- Just compare all pairs of points and keep track of the pair that gave the minimum distance.
- Runs in $O(n^2)$ time.
Divide and Conquer Algorithm
Note
The algorithm we did in class assumed that the $x$ and $y$ values are distinct. Below we will outline how algorithm can be simply generalized to handle this more general case.
In the text below, names and annotations are purposefully kept the same as the lecture notes to maintain consistency.
Setup/Notation
We now setup notation that is needed to state the algorithm (and also point out what parts need to change to handle non-distinct $x$ and $y$ values.
- Let $P_x$ be the list of points sorted by lexicographic order (i.e. sort by $x$ co-ordinate first and for points with the same $x$ co-ordinate sort them by their $y$ co-ordinate), and let $P_y$ be the list of points sorted by $y$ coordinate.
Note
Note that the definition of $P_x$ is not the same as we did in class (where we just sorted by $x$ co-ordinate). Note that under the assumption that the $x$ co-ordinates are distinct, the order above matches the one we did in class.
- Let $(x^*,y^*)$ be the the middle element of $P_x$.
- We will divide the plane into two halves based on $(x^*,y^*)$. The points $(x,y)$ lexicographically smaller than $(x^*,y^*)$ goes into the left half (called $Q$ from here on) and the rest of the points go into the right half (called $R$ from here on).
Note
Note that the definition of $Q$ is not the same as we did in class (where we just made the decision based on the $x$ co-ordinate). Note that under the assumption that the $x$ co-ordinates are distinct, the order above matches the one we did in class.
- Under the more general definition of $Q$ and $R$ above, the following claim, which we say in class for the case of distinct $x$ values still holds and is left as an exercise. (The generalization is the obvious one.)
Exercise (for students)
Given $P_x$ and $P_y$ as above, compute $Q_x,Q_y,R_x$ and $R_y$ in $O(n)$ time.
Algorithm Idea
- Recursively, find the closest pair of points in $Q$ and $R$ (call them $q_1,q_2$ and $r_1, r_2$). Let \[\delta =\min(d(q_1, q_2), d(r_1, r_2)).\]
- We also need to consider crossing points between $Q$ and $R$, so we will consider a "box" that spans $x$ values from from $x^* -\delta$ to to $x^* +\delta$.
- If we sort the points in the box by their $y$ coordinates (note that this can be done in $O(n)$ time given $P_y$ and $\delta$), the lemma in KT (5.10) claims that any two points with a distance $< \delta$ cannot be more than $15$ indices away.
Note
The
Closest-in-boxalgorithm remains the same as the one we saw in class.
Overall Algorithm
Dynamic Programming
Here is one way to think about Dynamic Programming algorithm:
- Divide problem into subproblems.
- Solve each subproblem.
- Combine to get original solution.
Divide and Conquer v/s Dynamic Programming
The above outline looks a lot like divide and conquer! The table below lists the differences:
| Divide and Conquer | Dynamic Programming |
| Independent subproblems | Overlapping subproblems |
| Solve top down | Solve bottom up (or top down using memoization) |
| Usually recursive | Backtracking |
Example: Divide and Conquer vs. Dynamic Programming Solutions
Fibonacci Sequence
This is the sequence $0,1,1,2,3,5,8,13,\dots$.
More formally, the sequence is defined as for any $n\ge 2$: \[\text{fib}[n] = \text{fib}[n-1] + \text{fib}[n-2],\] with the base case \[\text{fib}[0] = 0 \text{ and } \text{fib}[1] = 1.\]
Below is the obvious recursive (or divide and conquer algorithm):
Divide and Conquer Algorithm
fib(n):
#Input: n
#Output: fib[n]
if n==0:
return 0
else if n==1:
return 1
else:
return fib(n-1) + fib(n-2)
Exercise (for home)
Show that the above algorithm ends up using $2^{\Omega(n)}$ additions.
Of course the above is wasteful since we re-solve the same fib(i) multiple times. In this case the dynamic programming algorithm is the obvious one you would think of given the original recursion for fib[n]. I.e.
Dynamic Programming Algorithm
#Input: n
#Output: fib[n]
fib[0]=0
fib[1]=1
for i = 2 to n:
fib[i] = fib[i-1] + fib[i-2]
return fib[n]
Note
The above algorithm has $O(n)$ additions and takes $O(n)$ space.
One should only need $O(1)$ amount of space if one only keeps track of the last two elements.
A Digression
The stuff below is not relevant to dynamic programming but is a neat trick that you should know that is helpful in solving certain recursions.
Even faster computation
It turns out that one can compute fib[n] with $O(\log{n})$ multiplications and additions.
The trick in arguing the above is to use matrix-vector multiplication (recall Homework 0). In particular, first represent the recurrence for fib[n] as a matrix vector product, like so
\[\begin{pmatrix} \text{fib}[n]\\ \text{fib}[n-1]\end{pmatrix} = \begin{pmatrix} 1 & 1\\ 0 &1\end{pmatrix} \cdot \begin{pmatrix} \text{fib}[n-1]\\ \text{fib}[n-2]\end{pmatrix}.\]
Exercise 1
Convince yourself that the above identity holds.
Now, let us define the $2\times 2$ matrix: \[ M = \begin{pmatrix} 1 & 1\\ 0 &1\end{pmatrix}.\] In other words, one can re-state the identity above as \[\begin{pmatrix} \text{fib}[n]\\ \text{fib}[n-1]\end{pmatrix} = M \cdot \begin{pmatrix} \text{fib}[n-1]\\ \text{fib}[n-2]\end{pmatrix}.\] This implies the following identity
Identity
\[\begin{pmatrix} \text{fib}[n]\\ \text{fib}[n-1]\end{pmatrix} = M^{n-1}\cdot\begin{pmatrix} \text{fib}[1]\\ \text{fib}[0]\end{pmatrix}.\]Exercise 2
Convince yourself that the above identity holds.
Next we note that $M^{n-1}$ can be computed very efficiently:
Exercise 3
Argue that $M^{n-1}$ can be computed with $O(\log{n})$ additions and multiplications.
Hint
Generalize the algorithm for Question 1 on Homework 6.
We are now ready to show that fib[n] can be computed very efficiently:
Exercise 4
Show that $\text{fib}[n]$ can be computed with $O(\log{n})$ additions and multiplications.
Homework 7, Question 1
Chapter 6, Ex 2
The input are pairs $(\ell_i,h_i)$ for $i\in [n]$. For each week $i$, your algorithm has to decide if to pick a low-stress job (in which case you will get $\ell_i$ dollars) or pick a high stress job (in which case you will get $h_i$ dollars but you should not have chosen any job) or not pick any job (in preparation for a high stress job in week $i+1$). The goal of the algorithm is to maximize the total dollars it can collect.
Part (a)
The problem
Consider the following natural algorithm (where we define $h_i=\ell_i=0$ for any $i> n$):
Incorrect Greedy Algorithm
i=1
while i <= n
if hi+1 > li+li+1
Choose no job for week i
Choose high stress job for week i+1
i += 2
else
Choose low stress job for week i
i += 1
As the name of the algorithm above suggests, it is not a correct algorithm. Present an example input, where the algorithm above does not produce a plan that generates the most amount of dollars. You should state what the algorithm above outputs as well as state what the maximum value a plan can generate from your example input.
Counter Example Idea
Even though this is not required for your submission, we give the basic idea behind the counter-example. The main issue with the algorithm above is that it does not look into the future. So the algorithm can choose a high stress job in week $i$ without checking if it would be better to take a high stress job in week $(i+1)$ (if e.g. $h_{i+1}\gg h_i$).
Counter Example Details
Consider the following input:
| $i$ | $1$ | $2$ | $3$ |
| $\ell$ | $1$ | $1$ | $1$ |
| $h$ | $1$ | $3$ | $100$ |
Counter Example Argument
We need to argue two things:
- We claim that the optimal plan is to pick either low or high stress job in week $1$, no job in week $2$ and high stress job in week $3$ for a total of $1+100=101$ dollars. Even though this is not needed for your solution, here is a quick argument-- note that the optimal solution has to pick the high stress job on week $3$ (as otherwise even with all other jobs put together we will not be even close to $100$ dollars. Now once we choose high stress job in last week, we cannot choose any job in week $2$. Then for week $1$ we can pick either the low or high stress job.
- Now we have to argue that the plan returned by greedy algorithm will have a smaller value. This is left to you as an exercise:
Exercise 1
State the plan output by the greedy algorithm on the counter-example above, what is its total value and why the greedy algorithm will pick your claimed plan.
Part (b)
You will need to design a dynamic program to solve the original problem (recall that you only need to output the optimal value: i.e. you do not need to output the corresponding plan. We will leave you with two hints:
Hint
- For part (b) convince yourself that one should always schedule a job on the last day and then use it. If in your solution you use the hint, you will also have to convince the grader why you are convinced if you choose to use the hint, i.e. just using the hint as given (without any justification) will result in loss of points.
- The argument we presented above for why the claimed optimal solution in part (a) is indeed optimal, could be useful in figuring the recurrence relation for the optimal value.
Homework 7, Question 2
For sake of completeness, we repeat the general problem statement:
The Problem
We come back to the issue of many USA regions not having high speed internet. In this question, you will consider an algorithmic problem that you would need to solve to help out a (fictional) place
SomePlaceInUSAget high speed Internet. Fortunately, the town has secured a small grant to install a high speed Internet connection to one computer in the town's library. In this problem you will explore how effectively the town can share the resource of this one computer among the needy citizens ofSomePlaceInUSAin order to maximize the social good that this computer with high speed Internet connection can provide to the town as a whole.Residents of
SomePlaceInUSAhave applied to use the library's high speed Internet computer. Each of the $n$ citizens provide the following information. The $i$'th citizen submits a tuple $(s_i,f_i,w_i)$, where $s_i$ and the $f_i>s_i$ are the start and finish times of when the applicant plans to use the computer every weekday; $w_i$ is their estimation of the worth of getting to use the terminal from $s_i$ to $f_i$. (Note: the larger the value of $w_i$ the better for citizen $i$ and you can assume that $w_i\ge 0$ are integers.)Your initial goal is to determine the maximum worth among all
validsubset of citizens $S\subseteq [n]$. A subset $S$ isvalidif the start and finish times of any citizen $i\neq j\in S$ do not conflict (i.e. either $s_i> f_j$ or $s_j> f_i$). Further, the worth of a subset is \[w(S)=\sum_{i\in S} w_i.\]However, as time goes by the town realizes that solving the above problem is not necessarily the best for the overall good of the town. In the rest of the problem, you will design algorithms to maximize the total worth of your chosen subset along with some additional constraints to address some potential inequalities in your solution.Sample Input/Output
Here is a sample input/output pair (the input array is stated as $[(s_1,f_1,w_1),\dots,(s_n,f_n,w_n)]$) for $n=3$:
-
Input:$[(1,4,10),(5,10,20),(1,10,100)]$.
Output:$100$ (for the subset $\{3\}$).
Part (a)
The Problem
Citizens of
SomePlaceInUSArealize that the current problem as stated above could be monopolized by a citizen who (perhaps legitimately) can get a huge worth by using the computer terminal for the entire day. They come to you to help them solve the following updated version of the problem:- The input to your algorithm is now the set of triples $\{(s_i,f_i,w_i)|i\in [n]\}$ along with an integer threshold $\tau\ge 0$. Your algorithm should
output the maximum worth among all
validsubset $S\subseteq [n]$ with $|S|\ge \tau$. and output one with the maximum worth among all suchvalidsubsets (of size at least $\tau$). Note that the optimal worth can be $0$ (if there is novalidsubset of size at least $\tau$). -
Input:$2;[(1,4,10),(5,10,20),(1,10,100)]$.
Output:$30$ (for valid subset $\{1,2\}$). -
Input:$3;[(1,4,10),(5,10,20),(1,10,100)]$.
Output:$0$ (since there is no valid subset of size $3$).
Sample Input/Output
Here is a sample input/output pair (the input is stated as $\tau;[(s_1,f_1,w_1),\dots,(s_n,f_n,w_n)]$):
Algorithm Idea
We first make the observation that if we have $\tau=0$, then we have to find the maximum worth among all
validsubsets. However, note that in this case we exactly have the weighted interval scheduling problem, where the value of the $i$'th interval $[s_i,f_i]$ is $w_i$.So the main idea is to extend the notion of sub-problems from the weighted interval scheduling problem to handle the extra constraint of the lower bound on the size of the subset. In particular let $OPT(j,t)$ denote the maximum worth among all
validsubsets of size at least $t$ for the sub-problem where we are only given $(s_1,f_1,w_1),\dots,(s_j,t_j,w_j)$ as the input (i.e. we only consider the first $j$ citizens). All we now need to do is to determine the recurrence relation and note that the algorithm needs to output $OPT(n,\tau)$.We start off with the base case. Note that if $t> j$, then there is no possible
validsolution of size $t$ and hence we set $OPT(j,t)=-\infty$. Also trivially $OPT(0,0)=0$.Let us now consider the general case with $t\le j$. We now have two choices:
- Case 1: $j$ is not in any optimal
validsubset. In this case, we have that $OPT(j,t)=OPT(j-1,t)$. The argument is similar to what we had for similar case for the weighted interval scheduling: for sake of contradiction assume that $OPT(j,t) > OPT(j-1,t)$ and since any optimal solution achieving this worth does not have $j$ in it, such a solution would also be a valid solution for the input with the fist $j-1$ citizens (and same threshold of $t$), which would contradict the definition of $OPT(j-1,t)$. - Case 2: $j$ is in some optimal
validsubset (let's call this optimal subset $\mathcal{O}_j$). Then the claim is that $w(\mathcal{O}_j\setminus \{j\})=OPT(p(j),t-1)$, where $p(j)$ is defined exactly as it is for the weighted interval scheduling problem. The argument again follows from a similar argument that we used in this case for the weighted interval scheduling problem. In particular, we claim that $\mathcal{O}_j\setminus \{j\}$ is also an optimal solution for the input on the first $p(j)$ citizens and a threshold of $t-1$ (if not, there exists a solution $\mathcal{O}'$ that has worth $> w(\mathcal{O}_j\setminus \{j\}$ is better for this smaller problem instance. In such a case, note that $\mathcal{O}' \cup \{j\}$ is a valid solution for the problem on the first $j$ citizens and threshold $t$ and has value $> w_j + w(\mathcal{O}_j\setminus \{j\} = w(\mathcal{O}_j)$, which contradicts the fact that $\mathcal{O}_j$ is optimal for the $(j,t)$ sub-problem.) Thus, we have $OPT(j,t)=w_j+OPT(p(j),t-1)$ in this case.
So overall the recurrence for the optimal worth is given by (for $0\le j,t\le n$): \[OPT(j,t)=\begin{cases} -\infty & \text{ if } j< t \\ 0 & \text{ if } j=t=0\\ \max\left\{ OPT(j-1,t), w_j+OPT(p(j),t-1)\right\} & \text{otherwise} \end{cases}.\] To finish off the algorithm idea note that we can compute all the $OPT(\cdot,\cdot)$ values if we compute them increasing order of $j$ (for each fixed $j$, the order of $t$ does not matter). Finally, we just output $\max(0,OPT(n,\tau))$ (we do the $\max$ to make sure if the value of $OPT(n,\tau)=-\infty$, then we make it $0$ as required by the problem statement).
Algorithm Details
Even this is not needed in your solution, we present the algorithm details below:
# Input: Integers t, n and triples (s1, f1, w1), ..., (sn, fn, wn) # Also assume we know p(j) for every j = 0 .. n if t > n return 0 Allocate an (n+1) X (n+1) array M #M[j][k] will ultimately store OPT(j,k) M[0][0]=0 for every k = 1 .. n M[0][k] = -infty for every j = 1 .. n for every k = 0 .. n if j < k M[j][k] = -infty else M[j][k] = max ( M[j-1][k], wj + M[p(j)][k-1] return max(M[n][t],0)We are almost done with part (a) except for the following, which is left as an exercise for you:
Exercise 2
Argue that the above algorithm runs in $O(n^2)$ time.
Part (b)
The Problem
Citizens of
SomePlaceInUSArealize that the current problem as stated above might not be representative of their town. In particular, they would like thevalidsubset to be representative of the economic diversity of their town. In particular, now they want your solution to meet some more requirements:-
The input to your algorithm is now the set of $4$-tuples $\{(s_i,f_i,w_i,e_i)|i\in [n]\}$ (where $s_i,f_i,w_i$ are as before and $e_i\in \{1,2,3\}$ being an identifier for the range of their household income) along with there real numbers $0\le \rho_1,\rho_2,\rho_3\le 1$ such that $\rho_1+\rho_2+\rho_3\le 1$. Your algorithm should output the maximum worth among all
validsubset $S\subseteq [n]$ with the following minimum requirement of the economic diversity-- for every $j\in [3]$, we must have \[\left|\{i\in S|e_i=j\}\right|\ge \rho_j\cdot |S|.\] Note that the optimal worth can be $0$ (if there is novalidsubset that can meet the economic diversity constraint). -
Input:$\left(\frac 13, \frac 12, 0\right);[(1,4,10,1),(5,10,20,2),(1,10,100,3)]$.
Output:$30$ (for the valid subset $\{1,2\}$). -
Input:$\left(\frac 13, \frac 13, \frac13\right);[(1,4,10,1),(5,10,20,2),(1,10,100,3)]$.
Output:$0$ ($\emptyset$ is the only valid subset that satisfies the economic diversity constraint).
Sample Input/Output
Here is a sample input/output pair (the input is stated as $(\rho_1,\rho_2,\rho_3);[(s_1,f_1,w_1,e_1),\dots,(s_n,f_n,w_n,e_n)]$):
We do not have much to say for part (b) except to say:
Hint
Try to extend the dynamic program of part (a) to work for part (b). It might be useful to think of each sub-problem being indexed by a $5$-tuple (where each entry in the tuple can have $O(n)$ possibilities).
Billboard Problem
Note
This problem is not on the homework. If there is time in the recitations, we will cover this to show you more examples for dynamic programming.
The Problem
There are $n$ sites for a billboard, each at a location $x_i$ and each site generates $r_i$ revenue. (You can assume that $x_1\le x_2\le \cdots \le x_n$.)
The goal is to pick a subset of sites that maximizes the total revenue with the constraint that if sites $x_i$ and $x_j$ (for any $i\neq j$) are chosen, then: $|x_i - x_j| > 5$.
Here is an example input:
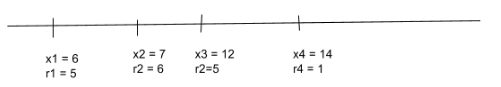
Bottom-Up (Dynamic Programming Style)
Consider the sub-problem, where we only have the first site:

Note that in this case the optimal solution is to pick the only site, which means he have $\text{OPT}(1) = 5$.Now consider the sub-problem where we have the first two sites
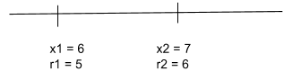
In the above case, we have two options:
- If we don’t pick site $2$, then the optimal solution is the same as above and we get $\text{OPT}(1)=5$.
- If on the other hand, we pick site $2$, we have to eliminate all sites within a 5 mile radius of site $2$ (which in this case is site $1$) and we get a revue of $r_2=6$.
Now consider the sub-problem where we have the first three sites
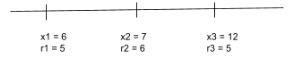
We again two two options:
- Do not pick site $3$, in which case we get revenue $\text{OPT}(2)$.
- Pick site $3$, in which case we will have to eliminate site $2$ and get a total revenue of $\text{OPT}(1) + r_3$.
Generic Formula
Note to TA
Try to get students to come up with this for you.
 We get the following recurrence: \[\text{OPT}(j) = \max\{\text{OPT}(j-1), \text{OPT}(e_j)+r_j\}.\]
We get the following recurrence: \[\text{OPT}(j) = \max\{\text{OPT}(j-1), \text{OPT}(e_j)+r_j\}.\]Definition
For any $j\in [n]$, define $e_j$ to be the closest site that is outside of $5$ mile radius from site $j$. That is, $e_j$ is the largest $i < j$ such that $x_i < x_j-5$.
In parallel with the weighted interval scheduling problem, the above recurrence leads to the following algorithm:
Dynamic Programming Algorithm
#Input: x[] and r[] #Output: OPT(n) M = [ ] #Stores value of OPT M[0] = 0 M[1] = r1 compute e[j] for j = 1..n #This can be done in O(n) time for j = 2...n: M[j] = max( M[j-1], M[e[j]] + r[j]) return M[n] #This will be the largest revenue$O(n)$ Runtime Analysis
Exercise (for home)
Given $x_1\le x_2\le \cdots x_n$, compute $e_j$ for $j\in [n]$ in $O(n)$ time.
Hint
If all the $x_j$'s are integers then this is simple. If not (i.e. if the $x_j$ can be real numbers), then consider the following. Create a new list of values $y_j=x_j-5$ for $j\in [n]$. Then merge the $x$ and $y$ arrays (note they both are sorted) and then use this merged sorted array to compute the $e_j$ values.
Given the above it is easy to see that the algorithm can be implemented in $O(n)$ time.