Automated Finite Element Discretization and Solution of Nonlinear Systems
PETSc
|
I have been a member of the PETSc Team since 1997. PETSc is an open-source software package designed for the solution of partial differential equations and used in diverse applications from surgery to environmental remediation. PETSc is the most complete, most flexible, most powerful, and easiest-to-use platform for solving the nonlinear algebraic equations arising from the discretization of partial differential equations. PETSc is designed to allow engineers and scientists to perform large-scale numerical simulations of physical phenomena rapidly and efficiently. Representative simulations to date include fluid flow for aircraft, ship, and automobile design; blood flow simulation for medical device design; porous media flow for oil reservoir simulation for energy development and groundwater contamination modeling; materials properties; economic modeling; structural mechanics for construction design; combustion modeling; and nuclear fission and fusion for energy development. These simulations allow the effects of design decisions to be evaluated and compared, including cost benefits, safety concerns, and environmental impact. PETSc has enabled simulations by industry, universities, and research laboratories, from desktop systems to the most powerful supercomputers, and for critical applications affecting the nation's energy, environment, and health. A testament to the widespread recognition of this package is the fact that PETSc has had over 400 downloads per month during the past three years. A Google search for "PETSc" on September 1, 2014, showed 223,000 pages referencing PETSc. In addition, a search of Google books found 662 books that reference PETSc. PETSc won the SIAM/ACM Prize in Computational Science and Engineering in 2015, and the R & D 100 Award in 2009. PETSc solvers were cited as one of the Top Ten Computational Science Accomplishments of the U.S. Department of Energy (DOE) in 2008. Two HPC hardware companies, Cray and SiCortex, provide and support PETSc with their products. Several commercial simulation packages, including FIDAP 8.5, TigerCAD, and RF3P, use PETSc for their algebraic solvers. Also, products from the companies Tech-X and Actel use PETSc. Microsoft has distributed previous versions of PETSc with its HPC software suite, the Microsoft Cluster CD. PETSc has been used by Boeing for computational fluid dynamics simulations and Shell for solving inverse problems for oil reservoir management. CFDResearch in Huntsville, Alabama, uses PETSc in its fluid simulations. PETSc solvers have also been used at the U.S. Army Engineering Research and Development Center and by the South Florida Water Management District modeling the Everglades. |
Linear and Nonlinear Preconditioning
|
Barry Smith, Peter Brune, Xuemin Tu, Jed Brown, and I are working on approaches to nonlinear preconditioning. Our approach is described in this paper. The most important aspect here is composability. This is exactly what makes KSP/PC so useful. Complex, optimal solvers can be built from simple pieces. We would like to carry over this design to the nonlinear problem. Our ideas for linear multiphysics preconditioning are contained in this paper and some follow-on work by Peter and Jed about very efficient Jacobian approximation and lagging. We now have a PETSc implementation of nonlinear preconditioning, e.g. SNESSetNPC() sets a nonlinear preconditioner, which support both left and right preconditioning, and also additive and multiplicative combinations of nonlinear solvers. Our paper detailing the preconditioners, has just been submitted. You can also see an example of me using this in a recent talk. This paper describes the PETSc approach to linear preconditioning for multiphysics systems. We show that our existing preconditioners can be composed to generate all previously published block preconditioners, and also to invert this relationship so that block preconditioners can be used on each level of multigrid or FAS. This talk decmonstrates how to construct these preconditioners for the Stokes equation, and here I construct an unstructured FAS cycle for the p-Laplacian using only command line options. We have the ability to attach auxiliary operators to the DM so that they can be used for preconditioning blocks of the system. Building on the FEM pieces described below, we will soon be able to form analytic approximations to operator blocks. For several years now, I have developed the BIBEE approximation for boundary integral operators with Jay Bardhan. This strategy approximates the surface-to-surface operator directly, and thus can provide good bounds for both the large and small eigenvalues. This is detailed in the page on biological applications. |
|
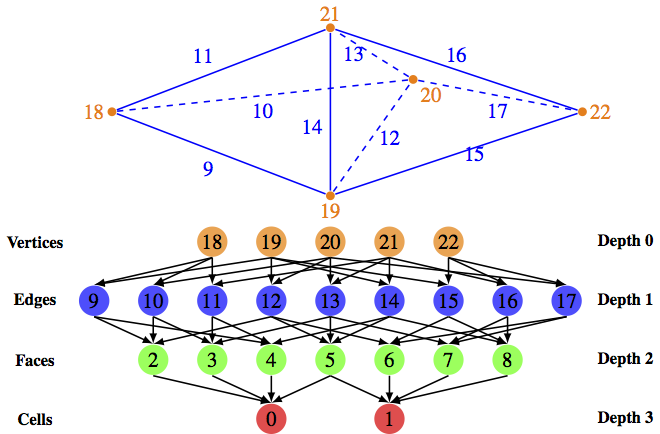
Mesh Representation and Manipulation
|
I developed the unstructured mesh support in PETSc, which is embodied by the DMPlex class. DMPlex can represent any CW complex, which is a much wider class of discretized surfaces than typically used in simulations, e.g. it can handle non-orientable and non-manifold surfaces, and uses hybrid meshes with prisms in PyLith. DMPlex can automatically create faces and edges for cell-vertex meshes, which I call mesh interpolation. In PyLith, it automatically inserts prismatic cells for use in the cohesive cell formulation of fault mechanics. It can also extract surfaces and volumes, create ghost cells, find boundaries, and orient meshes in parallel. It interfaces with most common mesh formats, and can output to HDF5 in parallel. You might want to configure with --download-triangle --with-ctetgenfor automatic mesh generation, partitioning, and output. DMPlex is intended not just to be a mesh representation, but a concise, powerful API for manipulating meshes and data over meshes. In fact, mesh topology is just seen as another field over the mesh points. In DMPlex, data can be mapped to any set of points using a PetscSection object. The parallel topology of this data is then encoded in a PetscSF. The data itself resides in a normal Vec or IS object. With these simple tools, we can build complex parallel data layouts, and easily enable operations such as load balancing, overlap increase, and mesh adaptivity in parallel. A forthcoming paper with Michael Lange and Gerard Gorman will discuss this in detail. This work rests on the DMPlex API for unstructured mesh representation and manipulation, detailed in this paper. Here is another paper by Anders Logg discussing his implementation of these ideas in FEniCS. Lawrence Mitchell and Michael Lange have done great work incorporating DMPlex into Firedrake as the mesh backend. DMPlex interfaces with the discretization code described below, and is intended for multiphysics simulation. You can run a full set of PDE tests using the new Python test system python2.7 ./config/builder2.py check src/snes/examples/tutorials/ex12.cThe test suite exhibits all the traditional preconditioners for the iso-viscous Stokes problem using PC FieldSplit (command lines), as well as matrix-free application of the operator combined with user-defined preconditioning, along with an FAS example using the p-Laplacian. For several years now, we have been exploring unstructured geometric coarsening, and its application to unstructured multigrid methods. Peter Brune has taken the lead on this work. Our recent paper shows simple applications of these ideas, but we would like to extend this to incorporate AMG ideas and also to larger and more complex problems. |
Discretization
|
I have recently introduced PETSc abstractions for quadrature, function spaces, dual spaces, and finite elements. Some good examples of this in PETSc are the Poisson equation with nonlinear coefficient and the Stokes equation on both simplicial and hexhedral meshes. Jed and I have also produced a 2nd order TVD finite volume example that can solve advection, shallow water, and the Euler equations with a variety of limiters and least-squares reconstruction. The discretization interface plays well with the DM interface for topology representation. This lets the user specify boundary conditions on any marked part of the boundary, automatically refine the mesh in parallel, create interpolation operators for the mesh hierarchy, and extract submanifolds from computation or visualization. In fact, SNES ex12 showcases an automatically assembled FAS (nonlinear multigrid) scheme for the p-Laplacian. The user need only specify the equations and boundary conditions as pointwise functions, and PETSc can assemble the rest. This is very much like the FEniCS approach. For example, the functions for Stokes:
void f1u(PetscScalar u[], PetscScalar gradU[], PetscScalar a[], PetscScalar gradA[],
PetscReal x[], PetscScalar f1[]) {
for (comp = 0; comp < Ncomp; ++comp) {
for (d = 0; d < dim; ++d) f1[comp*dim+d] = gradU[comp*dim+d]; /* (grad v, grad u) */
f1[comp*dim+comp] -= u[Ncomp]; /* (grad v, -p */
}
}
void f1p(PetscScalar u[], PetscScalar gradU[], PetscScalar a[], PetscScalar gradA[],
PetscReal x[], PetscScalar f0[]) {
f0[0] = 0.0;
for (d = 0; d < dim; ++d) f0[0] += gradU[d*dim+d];
}
And the boundary condition can be specified using:
void quadratic_u_2d(const PetscReal x[], PetscScalar *u, void *ctx)
{
u[0] = x[0]*x[0] + x[1]*x[1];
u[1] = 2.0*x[0]*x[0] - 2.0*x[0]*x[1];
}
Note that this strategy of using a pointwise specification of the problem is excellent for problems of
moderate complexity, but does not cover everything. However, the residual/Jacobian evaluation interface is
nicely hierarchical, and thus the user can decide how much of the infrastructure to use for their problem,
much like the rest of PETSc.
I collaborate with Jed Brown, Ridgway Scott, Andy Terrel, Peter Brune, and Robert Kirby on automation of finite element discretization, as well as better integration of mesh abstraction with discretization and solver routines. I am also involved with the FEniCS project at Simula Research, working in particular with Hans Petter Langtangen and Anders Logg. The overarching theme for this work is that automation in scientific computing, exemplified by compilers, should be raised to a higher level of abstraction. By confining ourselves to a well understood domain, in this case finite element methods, we can make the symbolic problem tractable. A prime example of this program is the FEniCS Form Compiler (FFC) which I use to generate GPU integration code in this paper. |
|
Papers
- This paper explains our framework for combining nonlinear solvers to generate scalable multilevel solvers for complex multiphysics problems. We develop both left and right nonlinear preconditioning, and discuss how previous work fits into our scheme. We have a composable implementation in PETSc so that all these new solvers can be built dynamically from the command line, just like PETSc linear preconditioners. We show examples of convergence acceleration using lid-driven cavity flow, large deformation elasticity, and the p-Laplacian.
- This paper describes the PETSc approach to multiphysics preconditioning. Using the PCFIELDSPLIT class, we are able to produce all the well-known block, or "physics-based", preconditioners. Furthermore, our design allows these block preconditioners to commute with multigrid so that we can provide segregated-KKT smoothers using the same infrastructure. In fact, the blocks given to PC FieldSplit can be arbitrary, so that this can also incorporate domain decomposition.
- This paper provides a provably \(\mathcal{O}(N)\) multigrid method based upon the coarsening developed by Dafna Talmor at CMU, with her advisor Gary Miller and Shang-Hua Teng. The 3D implementation cannot yet be shown to be \(\mathcal{O}(N)\) due to handling of the boundary, but our results show the optimal behavior.
- In this paper, we describe the Plex API for unstructured meshes, both representation and manipulation. It is very concise and can handle any cell complex, or anything that can be described with a Hasse diagram. As an example, we describe distributing meshes over a set of parallel processes, and also associated data, to demonstrate the power of the interface. We give examples of both hexahedral and simplicial meshes in 2D and 3D.
- In this paper, we introduce a novel splitting of the geometric and analytic parts of an element matrix. The geometric part changes for each cell, but is independent of the particular weak form. The analytic part depends on the weak form, but is independent of the mesh and can be calculated once and stored. We also address the question of optimizing the evaluation of these matrices. By finding redundant computations, we are able to significantly reduce the cost of building local stiffness matrices for the Laplace operator and for the trilinear form for Navier-Stokes operators. For the Laplace operator in two space dimensions, we have developed a heuristic graph algorithm that searches for such redundancies and generates code for computing the local stiffness matrices. Up to cubics, we are able to build the stiffness matrix on any triangle in less than one multiply-add pair per entry. Up to sixth degree, we can do it in less than about two pairs. Preliminary low-degree results for Poisson and Navier-Stokes operators in three dimensions are also promising.
- In this paper, we describe the implementation of general FEM residual evaluation using the Plex API. The intention is to write a single engine capable of supporting simplicial and hexhedral meshes, in any dimension, with an arbitrary element and weak form, coupled to scalable PETSc solvers. We believe this is possible using Plex.
- In this paper, we present some of the mathematical abstractions employed by automated modeling that allow a user to switch between finite elements, linear solvers, mesh refinement and geometry, and weak forms with very few modifications to the code. To evaluate the modularity provided by one of these abstractions, namely switching finite elements, we provide a numerical study based upon the many different discretizations of the Stokes equations. We also analyze the quality of the approximation with several measures.
- In this paper, Peter Brune, Ridgway Scott, and I show how to use prismatic elements in high dimensions to calculate some simple problems in eletronic structure explicitly.
Software
