The Fast Multipole Method and Radial Basis Function Interpolation
|
I collaborated with Felipe Cruz on the PetFMM code for simulation using the fast multipole method. The main idea is that a very simple serial implementation of FMM can be combined with optimization techniques from graph partitioning to produce an efficient and scalable parallel FMM. PetFMM completely reuses the serial code, and also uses templating to optimize the implementation. It templates over the structure used to describe source and targets, the neighborhood stencil, the expansion order, and the dimension. We are able to guide the optimization routine with good theoretical estimates of the communication and computation complexity. In fact, we hope to show that optimal communication complexity is achievable with PetFMM. I also worked with Rio Yokota and Andreas Klöckner on a version of FMM which would autogenerate expansions given the kernel function. We believe this is the step that most severely limits the wide adoption of the method. The implementation uses sympy for symbolic manipulation and code generation, and PyCUDA for kernel execution and organization. I also collaborated with Rio Yokota and Lorena Barba on the PetRBF code for parallel, radial basis function interpolation. PetRBF uses a scalable preconditioning strategy which uses small ASM blocks tailored to the function overlap. This code can interface with FMM libraries, or other fast evaluation schemes, to support large scale simulation. |
Papers
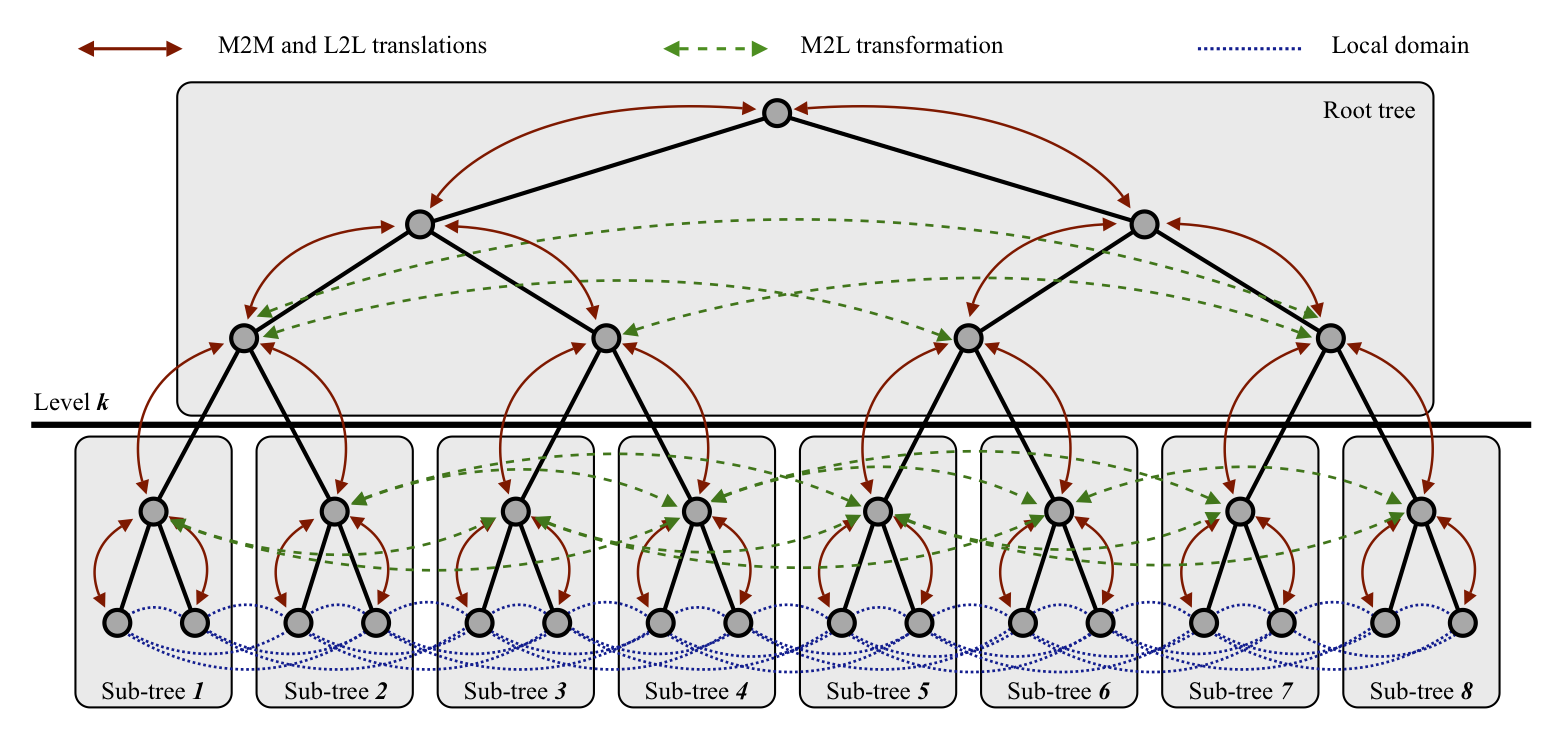
This paper details the main algorithms and code structure of PetFMM. It uses a novel application of graph paritioning to parallelize the tree traversal which permits complete reuse of the serial code for the parallel implementation. Fast algorithms for the computation of \(N\)-body problems can be broadly classified into mesh-based interpolation methods, and hierarchical or multiresolution methods. To this latter class belongs the well-known fast multipole method (FMM), which offers \(\mathcal{O}(N)\) complexity. The FMM is a complex algorithm, and the programming difficulty associated with it has arguably diminished its impact, being a barrier for adoption. This paper presents an extensible parallel library for \(N\)-body interactions utilizing the FMM algorithm. A prominent feature of this library is that it is designed to be extensible, with a view to unifying efforts involving many algorithms based on the same principles as the FMM and enabling easy development of scientific application codes.
The paper also details an exhaustive model for the computation of tree-based \(N\)-body algorithms in parallel, including both work estimates and communications estimates. With this model, we are able to implement a method to provide automatic, a priori load balancing of the parallel execution, achieving optimal distribution of the computational work among processors and minimal inter-processor communications. Using a client application that performs the calculation of velocity induced by \(N\) vortex particles in two dimensions, ample verification and testing of the library was performed. Strong scaling results are presented with 10 million particles on up to 256 processors, including both speedup and parallel efficiency. The largest problem size that has been run with the PetFMM library at this point was 64 million particles in 64 processors. The library is currently able to achieve over 85% parallel efficiency for 64 processes. The performance study, computational model, and application demonstrations presented in this paper are limited to 2D. However, the current code is capable of large, parallel 3D runs (see this paper). The software library is open source under the PETSc license, even less restrictive than the BSD license; this guarantees the maximum impact to the scientific community and encourages peer-based collaboration for the extensions and applications.
- We have written a paper with Dave May on calculating the gravity anomaly of a configuration using PetFMM. We describe three approaches for computing a gravity signal from a density anomaly. The first approach consists of the classical "summation" technique, whilst the remaining two methods solve the Poisson problem for the gravitational potential using either a Finite Element (FE) discretization employing a multilevel preconditioner, or a Green's function evaluated with the Fast Multipole Method (FMM). The methods utilizing the Poisson formulation described here differ from previously published approaches used in gravity modeling in that they are optimal, implying that both the memory and computational time required scale linearly with respect to the number of unknowns in the potential field. Additionally, all of the implementations presented here are developed such that the computations can be performed in a massively parallel, distributed memory computing environment. Through numerical experiments, we compare the methods on the basis of their discretization error, CPU time and parallel scalability. We demonstrate the parallel scalability of all these techniques by running forward models with up to \(10^8\) voxels on 1000's of cores.
- We have written a paper detailing the preconditioning method used to solve the RBF interpolation problem. We developed a parallel algorithm for radial basis function (RBF) interpolation that exhibits \(\mathcal{O}(N)\) complexity, requires \(\mathcal{O}(N)\) storage, and scales excellently up to a thousand processes. The algorithm uses a GMRES iterative solver with a restricted additive Schwarz method (RASM) as a preconditioner and a fast matrix-vector algorithm. Previous fast RBF methods --- achieving at most \(\mathcal{O}(N\log N)\) complexity --- were developed using multiquadric and polyharmonic basis functions. In contrast, the present method uses Gaussians with a small variance with respect to the domain, but with sufficient overlap. This is a common choice in particle methods for fluid simulation, our main target application. The fast decay of the Gaussian basis function allows rapid convergence of the iterative solver even when the subdomains in the RASM are very small. At the same time we show that the accuracy of the interpolation can achieve machine precision. The present method was implemented in parallel using the PETSc library. Numerical experiments demonstrate its capability in problems of RBF interpolation with more than 50 million data points, timing at 106 seconds (19 iterations for an error tolerance of \(10^{-15}\)) on 1024 processors of a Blue Gene/L (700 MHz PowerPC processors). The parallel code is freely available in the open-source model.