The Research Engineering Laboratory for Advanced Computational Science is a multidiscplinary center for the development of scalable algorithms and software tools for scientific simulation and engineering design. We are a partner lab with the Geodynamics Research and Visualization Laboratory (GRVL) in the Department of Geology.
We are devoted to the development and hardware optimization of scalable solvers for nonlinear PDEs and BIEs. We are a center of development for the PETSc libraries for scientific computing and the PyLith libraries for simulation of crustal deformation.
Seminar Series with GRVL Lab
Starting in 2020, RELACS will be hosting a joint seminar series with the UB Geodynamics Research and Visualization Lab, headed by Prof. Margarete Jadamec. This is paired with a seminar course focusing on numerical simulation, taught by Prof. Knepley and Prof. Jadamec. The seminar is held at 1pm EST on Wednesdays. The Zoom is not currently open, but please mail the conveners if you are interested in watching the talk.| Date | Speaker | Institution | Title | Abstract |
| Oct. 14th, 2020 | Mark Adams |
Lawrence Berkeley National Laboratory | Introduction to Textbook Multigrid Efficiency with Applications | We introduce textbook multigrid efficiency (TME) where systems of algebraic equations from discretized PDEs can be solved to discretization error accuracy with \(\mathcal{O}(1)\) work complexity, where the constant is a few work units or residual calculations. We discuss three research projects that build on these mathematical underpinnings to develop an HPC benchmark, a communication avoiding technique and a fast magnetohydrodynamic solver. First, we talk about the HPGMG benchmark developed with Sam Williams to provide a simple scalable benchmark that benefits from machines that are well balanced with respect to metrics that are relevant to application, such as memory bandwidth and communication latencies. Second, we talk about a communication avoiding technique that exploits the decay of the Green’s function for elliptic operators to maintain TME with less long-distance communication that classic multigrid. Finally, we discuss the application of classic multigrid methods to fully implicit resistive magnetohydrodynamic, with low resistivities, which are strongly hyperbolic equations, and observe near TME with about 20 work units complexity per time step. |
| Oct. 28th, 2020 | Scott MacLachlan |
Memorial University | Monolithic multigrid methods for magnetohydrodynamics | Magnetohydrodynamics (MHD) models describe a wide range of plasma physics applications, from thermonuclear fusion in tokamak reactors to astrophysical models. These models are characterized by a nonlinear system of partial differential equations in which the flow of the fluid strongly couples to the evolution of electromagnetic fields. As a result, the discrete linearized systems that arise in the numerical solution of these equations are generally difficult to solve, and require effective preconditioners to be developed. This talk presents recent work on mixed finite-element discretizations and monolithic multigrid preconditioners for a one-fluid, viscoresistive MHD model in two and three dimensions. In particular, we extend multigrid relaxation schemes from the fluid-dynamics literature to this MHD model and consider variants that are well-suited to parallelization. Numerical results will be shown for standard steady-state and time-dependent test problems. |
| Nov. 11th, 2020 | Carsten Burstedde |
Universität Bonn | TBD |
Sponsored Speakers
| Date | Speaker | Institution | Title | Abstract |
| Oct. 4th, 2018 | James Brannick | Pennsylvania State University | Algebraic Multigrid: Theory and Practice | This talk focuses on developing a generalized bootstrap algebraic multigrid algorithm for solving sparse matrix equations. As a motivation of the proposed generalization, we consider an optimal form of classical algebraic multigrid interpolation that has as columns eigenvectors with small eigenvalues of the generalized eigenproblem involving the system matrix and its symmetrized smoother. We use this optimal form to design an algorithm for choosing and analyzing the suitability of the coarse grid. In addition, it provides insights into the design of the bootstrap algebraic multigrid setup algorithm that we propose, which uses as a main tool a multilevel eigensolver to compute approximations to these eigenvectors. A notable feature of the approach is that it allows for general block smoothers and, as such, is well suited for systems of partial differential equations. In addition, we combine the GAMG setup algorithm with a least-angle regression coarsening scheme that uses local regression to improve the choice of the coarse variables. These new algorithms and their performance are illustrated numerically for scalar diffusion problems with highly varying (discontinuous) diffusion coefficient and for the linear elasticity system of partial differential equations. |
| Oct. 17th, 2017 | Jack Poulson | Google Inc. | Computing Cone Automorphisms in Interior Point Methods and Regularized Low-Rank Approximations | It is standard practice for (conic) primal-dual Interior Point Methods to apply their barrier functions to the Nesterov-Todd scaling point (a generalization of a geometric mean) of the primal and dual points; such a point is typically computed by applying the square-root of a cone automorphism that maps between the primal and dual point. A brief review of the correspondence between squares of Jordan algebras and symmetric cones will be provided, and an application of cone automorphisms to equilibrating regularized low-rank matrix factorizations will be provided (along with a scheme for its fast incorporation in an Alternating Least Squares algorithm). |
| Nov. 14th, 2017 | Stefan Rosenberger | University of Graz | SIMD Directived Parallelization for a Solver of the Bidomain Equations | Cardiovascular simulations include coupled PDEs (partial differential equations) for electrical potentials, non-linear deformations and systems of ODEs (ordinary differential equations) all of them are contained in the simulation software CARP (Cardiac Arrhythmia Research Package). We focus in this talk on the solvers for the elliptical part of the bidomain equations describing the electric stimulation of the heart for an anisotropic tissue. The existing conjugate gradient and GMRES solver with an algebraic multigrid preconditioner is already parallelized by MPI+OpenMP / CUDA. We investigate the OpenACC parallelization of this solver on one GPU especially its competitiveness with respect to the highly optimized CUDA implementation on recent GPUs. The OpenACC performance can achieve the CUDA performance if the implementation is especially careful written. Further, we show first results of the GPU parallelization with OpenMP 4.5. |
Sponsored Workshops
PETSc 2016
 |  |
The PETSc 2016 conference was the second in a series of workshops for the community using the PETSc libraries from Argonne National Laboratory (ANL). The Portable Extensible Toolkit for Scientific Computation (PETSc) is an open-source software package designed for the solution of partial differential equations and used in diverse applications from surgery to environmental remediation. PETSc 3.0 is the most complete, flexible, powerful, and easy-to-use platform for solving the nonlinear algebraic equations arising from the discretization of partial differential equations. The PETSc 2015 meeting at ANL hosted over 100 participants for a three day exploration of algorithm and software development practice, and the 2016 meeting had over 90 registrants.
We were fortunate to have very generous sponsors for this meeting. Thirteen student travel awards, including several international trips, were sponsored by Intel (through the Rice IPCC Center), Google, and Tech-X, and the conference facilities were sponsored by the Vienna Scientific Cluster. Richard Mills of Intel presented a keynote lecture on the new Knights Landing (KNL) architecture for the Xeon Phi line of processors and a strategy for PETSc performance optimization.
 |  |
 |  |
SIAM PP 2016 Minisymposium
Our minisymposium, To Thread or Not To Thread, attempted to clarifying the tradeoffs involved and give users and developers enough information to make informed decisions about programming models and library structures for emerging architectures, in particular the large, hybrid machines now being built by the Department of Energy. These will have smaller local memory/core, more cores/socket, multiple types of user- addressable memory, increased memory latencies (especially to global memory) and expensive synchronization. Two popular strategies, MPI+threads and flat MPI, need to be contrasted in terms of performance metrics, code complexity and maintenance burdens, and interoperability between libraries, applications, and operating systems.
- Threading Tradeoffs in Domain Decomposition, Jed Brown, Argonne National Laboratory and University of Colorado Boulder
- Firedrake: Burning the Thread at Both Ends, Michael Lange, Imperial College London
- Threads: the Wrong Abstraction and the Wrong Semantic, Jeff R. Hammond, Intel Corporation
- MPI+MPI: Using MPI-3 Shared Memory As a MultiCore Programming System, William D. Gropp, University of Illinois at Urbana-Champaign
- MPI+X: Opportunities and Limitations for Heterogeneous Systems, Karl Rupp, Vienna University of Technology
- The Occa Abstract Threading Model: Implementation and Performance for High-Order Finite-Element Computations, Tim Warburton and Axel Modave, Virginia Tech
Computational Infrastructure
The geosolver cluster at the Center for Computational Research is a 1200 core Dell/Linux machine with Intel Skylake processors connected by Intel Omni-Path fabric.| Processors | 100 Xeon 6126 |
| Memory | 9.4 TB of DDR4 |
| Memory Bandwidth | 8.4 TB/s |
| Local Disk | 12 TB |
| Network | Intel Omni-Path |
Team Members
| Prof. Matthew G. Knepley Group Lead | Research Areas | ||
 |
Computational Science Parallel Algorithms Limited Memory Algorithms Bioelectrostatic Modeling Computational Geophysics Computational Biophysics Unstructured Meshes Scientific Software PETSc Development |
||
| Dr. Robert Walker Postdoctoral Scholar | Research Areas | Dr. Kali Allison Postdoctoral Scholar | Research Areas |
 |
Computational Geophysics Poroelasticity Poroelasodynamics Numerical Software PyLith Development |
 |
Computational Geophysics Earthquake Cycle Mantle and Crust Rheology Seismology PyLith Development |
| Albert Cowie Graduate Student | Research Areas | Joseph V. Pusztay Graduate Student | Research Areas |
 |
Computational Science Performance Modeling Software Benchmarking Scientific Software |
 |
Computational Science Particle Methods Computational Plasma Physics Scientific Software |
| Daniel Finn Graduate Student | Research Areas | Darsh K. Nathawani Graduate Student | Research Areas |
 |
Computational Astrodynamics Computational Plasma Physics Time integration |
 |
Computational Fluid Dyanmics Droplet Mechanics Numerical homogenization |
| Alexander Stone Graduate Student | Research Areas | Feng-Mao (Frank) Tsai Graduate Student | Research Areas |
 |
Machine Learning for PDE Function Representation Numerical homogenization GPU programming |
 |
Computational meshing Formal methods Automated proof and verification |
| Aman Timalsina Undergraduate Student | Research Areas | Rachel Bakowski Undergraduate Student | Research Areas |
 |
Computational topology/geometry |
 |
Computational Geophysics |
| Thomas Kowalski Undergraduate Student | Research Areas | ||
 |
Computational Geophysics |
Alumni
| Prof. Tobin Isaac Assistant Professor (GT) | Research Areas | Prof. Maurice Fabien Assistant Professor (UW) | Research Areas |
 |
Computational Science Parallel Algorithms Computational Geophysics Structured AMR Scientific Software p4est Development PETSc Development |
 |
PDE Simulation High Performance Computing Spectral Methods Discontinuous Galerkin Methods Multigrid Algorithms |
| Dr. Justin Chang Member of the Technical Staff (AMD) | Research Areas | Thomas Klotz Smith Detection | Research Areas |
 |
Computational Science Parallel Algorithms Subsurface Transport Performance Modeling Software Benchmarking Scientific Software |
 |
Computational Science Bioelectrostatic Modeling Computational Biophysics High Precision Quadrature |
| Jeremy Tillay Chevron | Research Areas | Kirstie Haynie USGS (Golden) | Research Areas |
 |
Computational Science Limited Memory Algorithms Segmental Refinement Multigrid Computational Analysis |
 |
Geophysical modeling Computational Geodynamics Geophysical data assimilation |
| Jonas Actor Member of the Technical Staff (SNL) | Research Areas | Eric Buras Head of Data Science and ML at Arkestro | Research Areas |
 |
Computational Biology Numerical PDE Function representation Functional analysis |
 |
Data Science Graph Laplacian Inversion |
Collaborators
| Dr. Jaydeep P. Bardhan Glaxo-Smith-Kline |
Dr. Barry F. Smith Argonne National Laboratory |
Dr. Mark Adams Lawrence Berkeley National Laboratory |
Prof. Jed Brown University of Colorado Boulder |
 |
 |
 |
 |
| Dr. Dave A. May University of Oxford |
Dr. Brad Aagaard USGS, Menlo Park |
Dr. Charles Williams GNS Science, New Zealand |
Prof. Boyce Griffith University of North Carolina, Chapel Hill |
 |
 |
 |
 |
| Prof. Richard F. Katz University of Oxford |
Prof. Gerard Gorman Imperial College London |
Dr. Michael Lange Imperial College London |
Prof. Patrick E. Farrell University of Oxford |
 |
 |
 |
 |
| Prof. Margarete Jadamec University at Buffalo |
Prof. L. Ridgway Scott University of Chicago |
Dr. Karl Rupp Rupp, Ltd. |
Prof. Louis Moresi University of Melbourne |
 |
 |
 |
 |
| Dr. Lawrence Mitchell Durham |
Dr. Amir Molavi Northeastern University |
Dr. Nicolas Barral Imperial College, London |
|
 |
 |
 |
Projects
 |
This Intel Parallel Computing Center (IPCC) focuses on the optimization of core operations for scalable solvers. Barry Smith has implemented a PETSc communication API that automatically segregates on-node and off-node traffic in order to avoid possible MPI overhead. Andy Terrel, Karl Rupp, and Matt Knepley have developed algoritms for vectorization of low-order FEM on low memory/core architectures such as Intel KNL and Nvidia GPUs. Jed Brown, Barry Smith, and Dave May have demonstrated exceptional performance for \(Q_2\) and higher order elements. Mark Adams, Toby Isaac, and Matt Knepley are curerntly optimizing Full Approximation Scheme (FAS) multigrid, applied to PIC methods as part of the SITAR effort. |
 |
The RELACS Team is focused on developing nonlinear solvers for complex, multiphysics simulations, using both Partial Differential Equations (PDE) and Boundary Integral Equations (BIE) in collaboration with Jay Bardhan. We are also developing solvers for Linear Complementarity Problems (LCP) and engineering design problems. We focus on using true multilevel formulations in the Full Approximation Scheme (FAS) multigrid formulation. Theoretically, we are interested in characterizing the convergence of Newton's Method over multiple meshes, as well as composed nonlinear iterations arising from Nonlinear Preconditioning (NPC). |
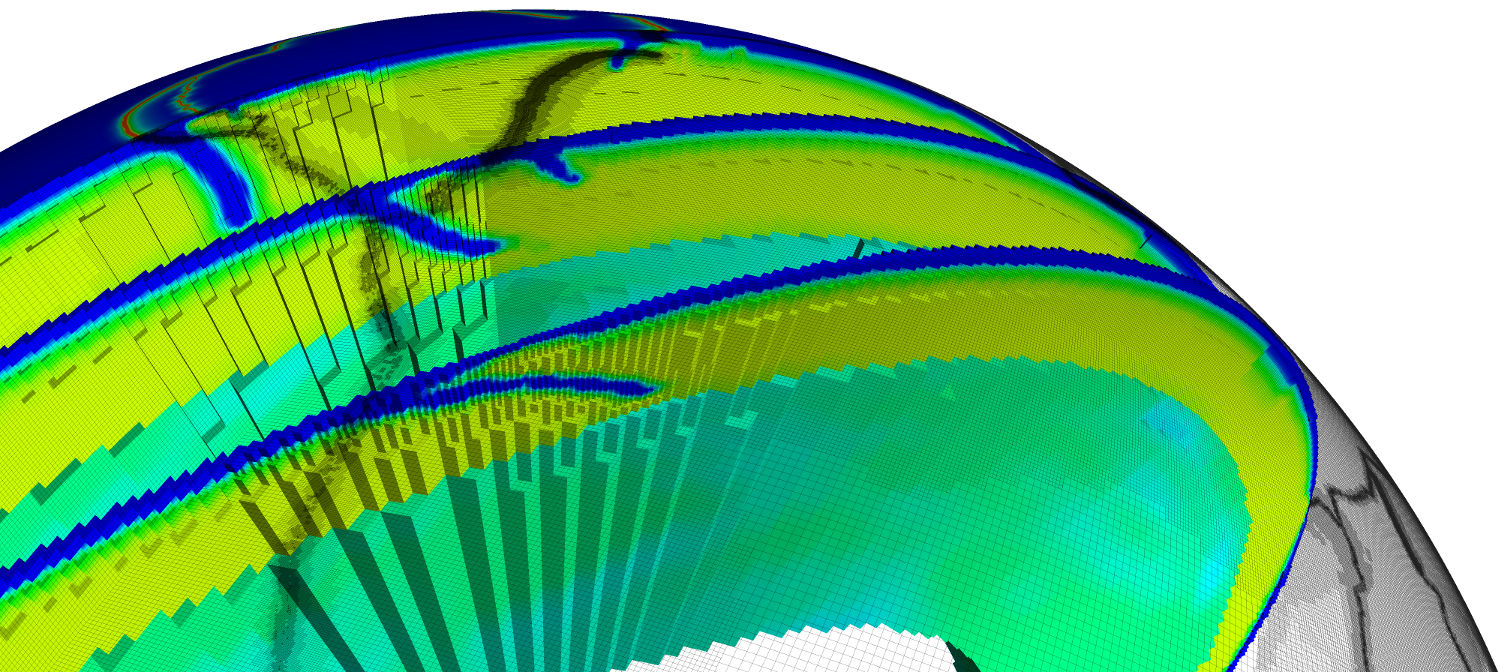 |
The Solver Interfaces for Tree Adaptive Refinement (SITAR) project aims to develop scalable and robust nonlinear solvers for multiphysics problems discretized on large, parallel structured AMR meshes. Toby Isaac, a core developer of p4est, has integrated AMR functionality into PETSc. Toby and Matt Knepley have implemented Full Approximation Scheme (FAS) multigrid for nonlinear problems for the AMR setting. Mark Adams and Dave May are adding a Particle-in-Cell (PIC) infrastructure to SITAR, targeting MHD plasma and Earth mantle dynamics simulations. |
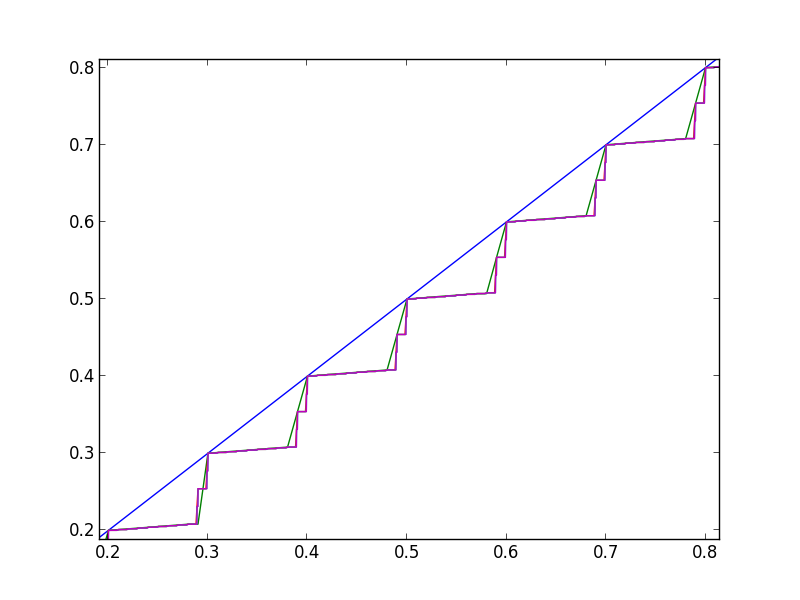 |
With the goal of reducing the dimension of difficult PDE problems, we are developing a new representation of multivariate continuous functions in terms of compositions of univariate functions, based upon the classical Kolmogorov representation. We are currently pursuing stronger regularity guarantees on the univariate functions, and also efficient algorithms for manipulating the functions inside iterative methods. |
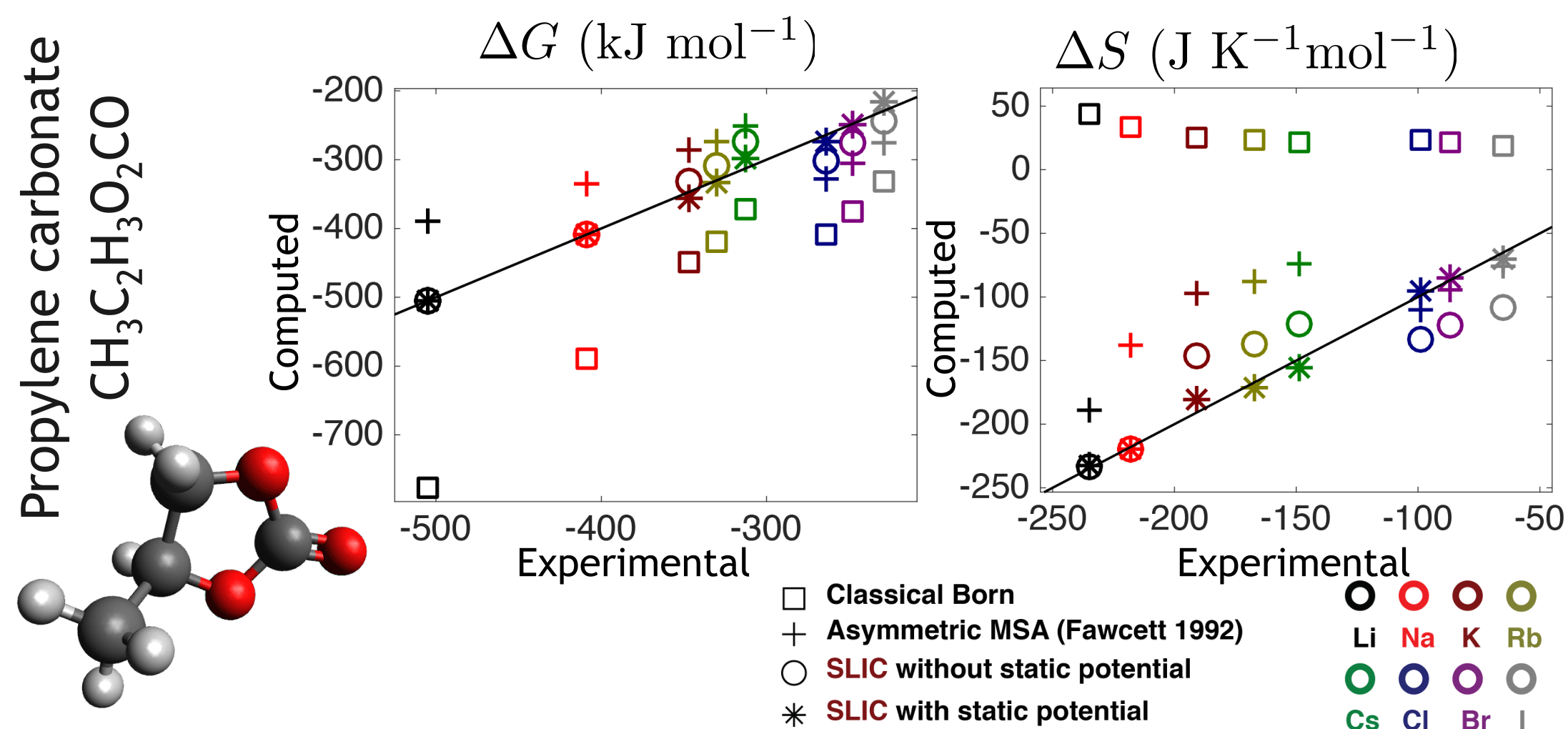 |
With Prof. Jaydeep Bardhan, we have developed a nonlinear continuum molecular electrostatics model capable of quantiative accuracy for a number of phenomena that are flatly wrong in current models, including charge-hydration asymmetry and calculation of entropies. To illustrate the importance of treating both steric asymmetry and the static molecular potential separately, we have recently computed the charging free energies (and profiles) of individual atoms in small molecules. The static potential derived from MD simulations in TIP3P water is positive, meaning that for small positive charges, the charging free energy is actually positive (unfavorable). Traditional dielectric models are completely unable to reproduce such positive charging free energies, regardless of atomic charge or radius. However, our model reproduces these energies with quantitative accuracy, and we note that these represent unfavorable electrostatic contributions to solvation by hydrophobic groups. Traditional implicit-solvent models predicate that hydrophobic groups contribute nothing; for instance, nonpolar solvation models are often parameterized under the assumption that alkanes have electrostatic solvation free energies equal to zero. We have found this to be not the case, and because our model has few parameters that do not involve the atom radii, we have been able to parameterize a complete and consistent implicit-solvent model, that is, parameterizing both the electrostatic and nonpolar terms simultaneously. We found that this model is remarkably accurate, comparable to explicit solvent simulations for solvation free energies and water-octanol transfer free energies. |
 |
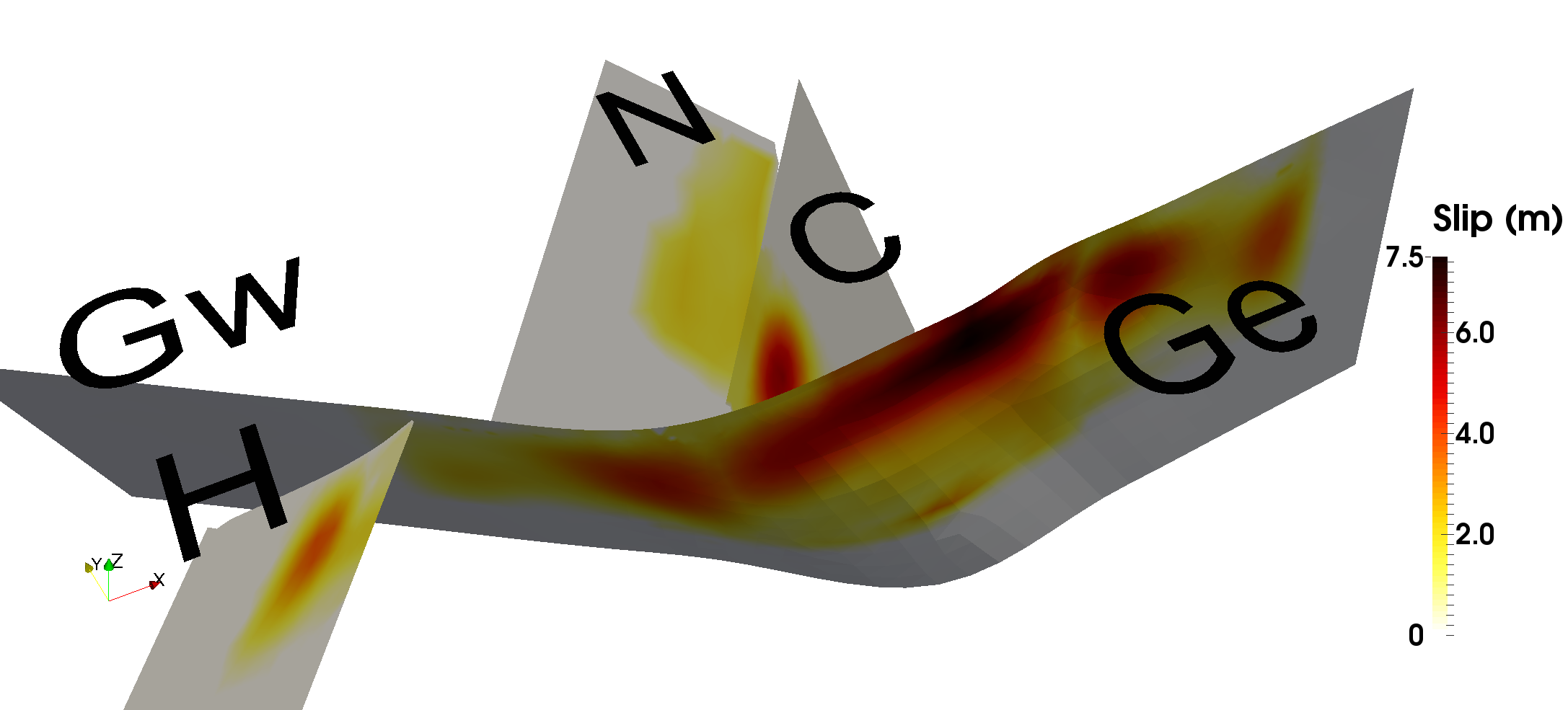
In collaboration with Richard Katz, we are working to scale solvers for Magma Dynamics simulations to large, parallel machines. The current formulation is an index 1 Differential-Algebraic Equation (DAE) in which the algebraic constraints are an elliptic PDE for the mass and momentum conservation, coupled to the porosity through permability and viscosities. We discretize this using continuous Galerkin FEM and our Full Approximation Scheme (FAS) solver has proven effective for the elliptic constraints. The advection of porosity is a purely hyperbolic equation coupled to the fluid velocity, which we discretize using FVM. The fully coupled nonlinear problem is solved at each explicit timestep. |
Sponsors
 |
 |
 |
 |
Great YouTube Videos
I have been really impressed by the quality of mathematics videos on YouTube. Some of my favorites are shown below. Do not hesitate to suggest ones that I have missed.| Excellent introduction to the connection between entanglement and wormholes, given by Leonard Susskind. | |
| Excellent introduction to climatic variation, given by Daniel Britt. | |
| Excellent introduction to the seismic inverse problem, given by Bill Symes. | |
| This talk looks at important physics contributions from Feynman, given by Leonard Susskind. | |
| Overview talk on the physics of Quantum Computing, given by John Preskill. | |
| Good talk on current work in Quantum Computing, given by Jarrod McClean. | |
| This talk is a celebration of Euler, the greatest (applied) mathematician of all time. William Dunham is a fantastic speaker and writer, and I own all of his books. | |
| Cedric Villani talks about entropy of gases. He starts from very simple concepts and builds up with straighforward language. His presentation is fantastic. | |
| Cedric Villani again, talking about John Nash. | |
| Mike Glazer talking about Perovskites. | |
| Emmanuel Candes at ICIAM 2014 talking about sparsity. | |
| Richard Feynamn gives the Douglas Robb Memorial Lecture from New Zealand 1979 | |
| Stan Osher accepts the Von Neumann Prize | You sadly need a SIAM account for this one |
| Lawrence Krauss, my old professor, on his book Hidden Realities | |
| Suzie Sheehy, talking about new kinds of particle accelerators | |
| Ian Morris, talking about the deep history of civilization, in Chicago | |
| Leonard Susskind, talking about Black Holes and the Holographic Principle, at Cornell | |
| Andrew George, talking about The Epic of Gilgamesh, at Harvard (along with some repsonses) | |
| Irving Finkel, talking about the Babylonian story of the Ark |
News
- Papers
- Paper in SIAM Review describing nonlinear preconditioning in PETSc.
- New paper modeling asymmetry in solvation free energies.
- PETSc
- Article about PETSc from ASCR
- The PETSc Core Development Group won the 2015 SIAM/ACM Prize in Computational Science and Engineering
- Article about PETSc in the DOE ASCR Newsletter